Hostname: page-component-cd9895bd7-mkpzs Total loading time: 0 Render date: 2024-12-24T00:26:43.008Z Has data issue: false hasContentIssue false
  • English
  • Français

Experimental and computational studies of the aerodynamic performance of a flapping and passively rotating insect wing

Published online by Cambridge University Press:  15 February 2016

Yufeng Chen ,
Nick Gravish ,
Alexis Lussier Desbiens ,
Ronit Malka  and
Robert J. Wood
Yufeng Chen*
Affiliation:
School of Engineering and Applied Sciences, Harvard University, Cambridge, MA 02138, USA
Nick Gravish
Affiliation:
School of Engineering and Applied Sciences, Harvard University, Cambridge, MA 02138, USA
Alexis Lussier Desbiens
Affiliation:
Department of Mechanical Engineering, Université de Sherbrooke, Sherbrooke, J1K 2R1, Canada
Ronit Malka
Affiliation:
School of Engineering and Applied Sciences, Harvard University, Cambridge, MA 02138, USA
Robert J. Wood
Affiliation:
School of Engineering and Applied Sciences, Harvard University, Cambridge, MA 02138, USA
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Flapping wings are important in many biological and bioinspired systems. Here, we investigate the fluid mechanics of flapping wings that possess a single flexible hinge allowing passive wing pitch rotation under load. We perform experiments on an insect-scale (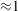${\approx}1$  cm wing span) robotic flapper and compare the results with a quasi-steady dynamical model and a coupled fluid–structure computational fluid dynamics model. In experiments we measure the time varying kinematics, lift force and two-dimensional velocity fields of the induced flow from particle image velocimetry. We find that increasing hinge stiffness leads to advanced wing pitching, which is beneficial towards lift force production. The classical quasi-steady model gives an accurate prediction of passive wing pitching if the relative phase difference between the wing stroke and the pitch kinematics, 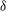${\it\delta}$, is small. However, the quasi-steady model cannot account for the effect of 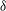${\it\delta}$ on leading edge vortex (LEV) growth and lift generation. We further explore the relationships between LEV, lift force, drag force and wing kinematics through experiments and numerical simulations. We show that the wing kinematics and flapping efficiency depend on the stiffness of a passive compliant hinge. Our dual approach of running at-scale experiments and numerical simulations gives useful guidelines for choosing wing hinge stiffnesses that lead to efficient flapping.

JFM classification

Aerodynamics: Aerodynamics Vortex Flows: Vortex shedding
Type
Papers
Information
Journal of Fluid Mechanics , Volume 791 , 25 March 2016 , pp. 1 - 33
Check for updates
Copyright
© 2016 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Alben, S. & Shelley, M. 2005 Coherent locomotion as an attracting state for a free flapping body. Proc. Natl Acad. Sci. USA 102 (32), 11163–11166.Google Scholar
Ashby, M. F.2011 Materials Selection in Mechanical Design. Butterworth-Heinemann.Google Scholar
Bergou, A. J., Xu, S. & Wang, Z. 2007 Passive wing pitch reversal in insect flight. J. Fluid Mech. 591, 321–337.CrossRefGoogle Scholar
Birch, J. M. & Dickinson, M. H. 2003 The influence of wing–wake interactions on the production of aerodynamic forces in flapping flight. J. Expl Biol. 206 (13), 2257–2272.Google Scholar
Bos, F. M., Lentink, D., Van Oudheusden, B. W. & Bijl, H. 2008 Influence of wing kinematics on aerodynamic performance in hovering insect flight. J. Fluid Mech. 594, 341–368.CrossRefGoogle Scholar
Cheng, B., Roll, J., Liu, Y., Troolin, D. R. & Deng, X. 2014 Three-dimensional vortex wake structure of flapping wings in hovering flight. J. R. Soc. Interface 11 (91), 20130984.Google Scholar
Dickinson, M. H. & Gotz, K. G. 1993 Unsteady aerodynamic performance of model wings at low Reynolds numbers. J. Expl Biol. 174 (1), 45–64.Google Scholar
Dickinson, M. H., Lehmann, F.-O. & Sane, S. P. 1999 Wing rotation and the aerodynamic basis of insect flight. Science 284 (5422), 1954–1960.Google Scholar
Dickson, W. B., Straw, A. D. & Dickinson, M. H. 2008 Integrative model of drosophila flight. AIAA J. 46 (9), 2150–2164.CrossRefGoogle Scholar
Ellington, C. P. 1984 The aerodynamics of hovering insect flight. III: kinematics. Phil. Trans. R. Soc. Lond. B 305 (1122), 41–78.Google Scholar
Ellington, C. P., Van Den Berg, C., Willmott, A. P. & Thomas, A. L. R. 1996 Leading-edge vortices in insect flight. Nature 384, 626–630.Google Scholar
Ennos, A. R. 1988 The importance of torsion in the design of insect wings. J. Expl Biol. 140 (1), 137–160.Google Scholar
Fienup, J. R. & Kowalczyk, A. M. 1990 Phase retrieval for a complex-valued object by using a low-resolution image. J. Opt. Soc. Am. A 7 (3), 450–458.Google Scholar
Fry, S. N., Sayaman, R. & Dickinson, M. H. 2003 The aerodynamics of free-flight maneuvers in drosophila. Science 300 (5618), 495–498.Google Scholar
Geuzaine, C. & Remacle, J.-F. 2009 Gmsh: a 3-d finite element mesh generator with built-in pre- and post-processing facilities. Intl J. Numer. Meth. Engng 79 (11), 1309–1331.CrossRefGoogle Scholar
Guilmineau, E. & Queutey, P. 2002 A numerical simulation of vortex shedding from an oscillating circular cylinder. J. Fluids Struct. 16 (6), 773–794.CrossRefGoogle Scholar
Henderson, R. D. 1995 Details of the drag curve near the onset of vortex shedding. Phys. Fluids 7 (9), 2102–2104.CrossRefGoogle Scholar
Hesthaven, J. S. & Warburton, T. 2007 Nodal Discontinuous Galerkin Methods: Algorithms, Analysis, and Applications. vol. 54. Springer.Google Scholar
Jensen, M. 1956 Biology and physics of locust flight. III: the aerodynamics of locust flight. Phil. Trans. R. Soc. Lond. B 239 (667), 511–552.Google Scholar
Jones, D. A. & Clarke, D. B.2008 Simulation of the flow past a sphere using the fluent code. Tech. Rep. DSTO-TR-2232. http://digext6.defence.gov.au/dspace/handle/1947/9705.Google Scholar
Kang, C.-k. & Shyy, W.2012 Passive wing rotation in flexible flapping wing aerodynamics. In Proceedings of the 30th AIAA Applied Aerodynamics Conference.Google Scholar
Keennon, M., Klingebiel, K., Won, H. & Andriukov, A.2012 Development of the nano hummingbird: a tailless flapping wing micro air vehicle. In 50th AIAA Aerospace Sciences Meeting Including the New Horizons Forum and Aerospace Exposition, Nashville, TN, January, pp. 9–12.Google Scholar
Lentink, D. & Dickinson, M. H. 2009 Rotational accelerations stabilize leading edge vortices on revolving fly wings. J.  Expl Biol. 212 (16), 2705–2719.Google Scholar
Lentink, D., Jongerius, S. R. & Bradshaw, N. L. 2010 The scalable design of flapping micro-air vehicles inspired by insect flight. In Flying Insects and Robots, pp. 185–205. Springer.Google Scholar
Ma, K. Y., Chirarattananon, P., Fuller, S. B. & Wood, R. J. 2013 Controlled flight of a biologically inspired, insect-scale robot. Science 340 (6132), 603–607.Google Scholar
Nakata, T. & Liu, H. 2011 Aerodynamic performance of a hovering hawkmoth with flexible wings: a computational approach. Proc. R. Soc. Lond. B 279 (1729), 722–731.Google Scholar
Persson, P.-O. & Strang, G. 2004 A simple mesh generator in matlab. SIAM Rev. 46 (2), 329–345.Google Scholar
Ramananarivo, S., Godoy-Diana, R. & Thiria, B. 2011 Rather than resonance, flapping wing flyers may play on aerodynamics to improve performance. Proc. Natl Acad. Sci. USA 108 (15), 5964–5969.CrossRefGoogle ScholarPubMed
Sane, S. P. & Dickinson, M. H. 2001 The control of flight force by a flapping wing: lift and drag production. J. Expl Biol. 204 (15), 2607–2626.Google Scholar
Spagnolie, S. E., Moret, L., Shelley, M. J. & Zhang, J. 2010 Surprising behaviors in flapping locomotion with passive pitching. Phys. Fluids 22 (4), 041903.CrossRefGoogle Scholar
Stojković, D., Breuer, M. & Durst, F. 2002 Effect of high rotation rates on the laminar flow around a circular cylinder. Phys. Fluids 14 (9), 3160–3178.CrossRefGoogle Scholar
Thielicke, W. & Stamhuis, E. J. 2015 The influence of wing morphology on the three-dimensional flow patterns of a flapping wing at bird scale. J. Fluid Mech. 768, 240–260.Google Scholar
Thiria, B. & Godoy-Diana, R. 2010 How wing compliance drives the efficiency of self-propelled flapping flyers. Phys. Rev. E 82 (1), 015303.Google Scholar
Tu, S. & Aliabadi, S. 2005 A slope limiting procedure in discontinuous Galerkin finite element method for gasdynamics applications. Intl J. Numer. Anal. Model. 2 (2), 163–178.Google Scholar
Wang, J. & Chang, S. 2013 Predicting fruit fly’s sensing rate from insect flight simulations. Bull. Am. Phys. Soc. 58 (1), 17002.Google Scholar
Wang, Z. J., Birch, J. M. & Dickinson, M. H. 2004 Unsteady forces and flows in low Reynolds number hovering flight: two-dimensional computations vs robotic wing experiments. J. Expl Biol. 207 (3), 449–460.Google Scholar
Whitney, J. P. & Wood, R. J. 2010 Aeromechanics of passive rotation in flapping flight. J. Fluid Mech. 660, 197–220.Google Scholar
Willert, C. E. & Gharib, M. 1991 Digital particle image velocimetry. Exp. Fluids 10 (4), 181–193.Google Scholar
Wood, R. J., Avadhanula, S., Sahai, R., Steltz, E. & Fearing, R. S. 2008 Microrobot design using fiber reinforced composites. J. Mech. Design 130 (5), 052304.Google Scholar
Zhang, J., Liu, N.-S. & Lu, X.-Y. 2010 Locomotion of a passively flapping flat plate. J. Fluid Mech. 659, 43–68.Google Scholar
Zhao, L., Huang, Q., Deng, X. & Sane, S. P. 2010 Aerodynamic effects of flexibility in flapping wings. J. R. Soc. Interface 7 (44), 485–497.Google Scholar
Zheng, L., Hedrick, T. L. & Mittal, R. 2013 A multi-fidelity modelling approach for evaluation and optimization of wing stroke aerodynamics in flapping flight. J. Fluid Mech. 721, 118–154.Google Scholar

Chen et al. supplementary movie

This movie shows a millimetre scale wing (wing span: 12.8mm, mean wing chord: 3mm) flapped at 120Hz. The first part illustrates the experimental setup and flapping kinematics. The movie also shows the particle velocimetry measurement of vorticity field and a numerical simulation using identical input kinematics.

Download Chen et al. supplementary movie(Video)
Video 23.7 MB
Supplementary material: PDF

Chen et al. supplementary material

Supplementary data

Download Chen et al. supplementary material(PDF)
PDF 166.9 KB

Chen et al. supplementary movie

This movie compares flapping experiments in air and in vacuum, at 120Hz. We show the passive pitching amplitude is much smaller in vacuum than it is in air. In addition, the pitching frequency is higher than driving frequency in vacuum.

Download Chen et al. supplementary movie(Video)
Video 7.3 MB