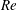Hostname: page-component-78c5997874-t5tsf Total loading time: 0 Render date: 2024-11-17T15:13:54.121Z Has data issue: false hasContentIssue false
  • English
  • Français

Existence of a sharp transition in the peak propulsive efficiency of a low-$Re$ pitching foil

Published online by Cambridge University Press:  07 July 2016

Anil Das ,
Ratnesh K. Shukla  and
Raghuraman N. Govardhan
Anil Das
Affiliation:
Department of Mechanical Engineering, Indian Institute of Science, Bangalore, 560012, India
Ratnesh K. Shukla*
Affiliation:
Department of Mechanical Engineering, Indian Institute of Science, Bangalore, 560012, India
Raghuraman N. Govardhan*
Affiliation:
Department of Mechanical Engineering, Indian Institute of Science, Bangalore, 560012, India
*
†Email addresses for correspondence: [email protected], [email protected]
†Email addresses for correspondence: [email protected], [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We perform a comprehensive characterization of the propulsive performance of a thrust generating pitching foil over a wide range of Reynolds (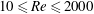$10\leqslant Re\leqslant 2000$) and Strouhal (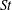$St$) numbers using a high-resolution viscous vortex particle method. For a given 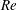$Re$, we show that the mean thrust coefficient 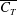$\overline{C_{T}}$ increases monotonically with 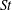$St$, exhibiting a sharp rise as the location of the inception of the wake asymmetry shifts towards the trailing edge. As a result, the propulsive efficiency too rises steeply before attaining a maximum and eventually declining at an asymptotic rate that is consistent with the inertial scalings of 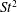$St^{2}$ for 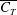$\overline{C_{T}}$ and 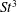$St^{3}$ for the mean power coefficient, with the latter scaling holding, quite remarkably, over the entire range of 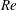$Re$. We find the existence of a sharp increase in the peak propulsive efficiency 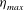${\it\eta}_{max}$ (at a given 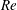$Re$) in the 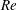$Re$ range of 50 to approximately 1000, with 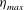${\it\eta}_{max}$ increasing rapidly from about 1.7 % to the saturated asymptotic value of approximately 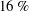$16\,\%$. The $St$ at which 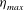${\it\eta}_{max}$ is attained decreases progressively with 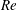$Re$ towards an asymptotic limit of 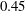$0.45$ and always exceeds the one for transition from a reverse von Kármán to a deflected wake. Moreover, the drag-to-thrust transition occurs at a Strouhal number 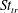$St_{tr}$ that exceeds the one for von Kármán to reverse von Kármán transition. 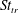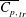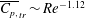The $St_{tr}$ and the corresponding power coefficient $\overline{C_{p,}}_{tr}$ are found to be remarkably consistent with the simple scaling relationships $St_{tr}\sim Re^{-0.37}$ and $\overline{C_{p,}}_{tr}\sim Re^{-1.12}$ that are derived from a balance of the thrust generated from the pitching motion and the drag force arising out of viscous resistance to the foil motion. The fact that the peak propulsive efficiency degrades appreciably only below 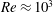$Re\approx 10^{3}$ establishes a sharp lower threshold for energetically efficient thrust generation from a pitching foil. Our findings should be generalizable to other thrust-producing flapping foil configurations and should aid in establishing the link between wake patterns and energetic cost of thrust production in similar systems.

JFM classification

Biological Fluid Dynamics: Propulsion Vortex Flows: Vortex shedding Wakes/Jets: Wakes/Jets
Type
Papers
Information
Journal of Fluid Mechanics , Volume 800 , 10 August 2016 , pp. 307 - 326
Check for updates
Copyright
© 2016 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Anderson, J. M., Streitlien, K., Barrett, D. S. & Triantafyllou, M. S. 1998 Oscillating foils of high propulsive efficiency. J. Fluid Mech. 360, 41–72.Google Scholar
Birch, J. M., Dickson, W. B. & Dickinson, M. H. 2004 Force production and flow structure of the leading edge vortex on flapping wings at high and low Reynolds numbers. J. Expl Biol. 207, 1063–1072.Google Scholar
Bohl, D. G. & Koochesfahani, M. M. 2009 MTV measurements of the vortical field in the wake of an airfoil oscillating at high reduced frequency. J. Fluid Mech. 620, 63–88.Google Scholar
Cottet, G.-H. & Koumoutsakos, P. 2000 Vortex Methods: Theory and Practice. Cambridge University Press.Google Scholar
Dewey, P. A., Boschitsch, B. M., Moored, K. W., Stone, H. A. & Smits, A. J. 2013 Scaling laws for the thrust production of flexible pitching panels. J. Fluid Mech. 732, 29–46.Google Scholar
Ehrenstein, U. & Eloy, C. 2013 Skin friction on a moving wall and its implications for swimming animals. J. Fluid Mech. 718, 321–346.Google Scholar
Ehrenstein, U., Marquillie, M. & Eloy, C. 2014 Skin friction on a flapping plate in uniform flow. Proc. R. Soc. Lond. B 372, 20130345.Google Scholar
Eldredge, J. D. 2007 Numerical simulation of the fluid dynamics of 2D rigid body motion with the vortex particle method. J. Comput. Phys. 221 (2), 626–648.CrossRefGoogle Scholar
Eldredge, J. D., Toomey, J. & Medina, A. 2010 On the roles of chord-wise flexibility in a flapping wing with hovering kinematics. J. Fluid Mech. 659, 94–115.Google Scholar
Gazzola, M., Argentina, M. & Mahadevan, L. 2014 Scaling macroscopic aquatic locomotion. Nat. Phys. 10, 758–761.Google Scholar
Godoy-Diana, R., Aider, J.-L. & Wesfreid, J. E. 2008 Transitions in the wake of a flapping foil. Phys. Rev. E 77 (1), 016308.Google Scholar
Godoy-Diana, R., Marais, C., Aider, J.-L. & Wesfreid, J. E. 2009 A model for the symmetry breaking of the reverse Bénard–von Kármán vortex street produced by a flapping foil. J. Fluid Mech. 622, 23–32.Google Scholar
Goude, A. & Engblom, S. 2013 Adaptive fast multipole methods on the GPU. J. Supercomput. 63 (3), 897–918.Google Scholar
Harbig, R. R., Sheridan, J. & Thompson, M. C. 2013 Reynolds number and aspect ratio effects on the leading-edge vortex for rotating insect wing planforms. J. Fluid Mech. 717, 166–192.Google Scholar
Heathcote, S. & Gursul, I. 2007 Flexible flapping airfoil propulsion at low Reynolds numbers. AIAA J. 45, 1066–1079.Google Scholar
Hunt, J. C. R., Wray, A. A. & Moin, P. 1988 Eddies, streams, and convergence zones in turbulent flows. In Center for Turbulence Research Report CTR-S88, pp. 193–208. NASA Ames/Stanford University Center for Turbulence Research.Google Scholar
Katz, J. & Weihs, D. 1978 Hydrodynamic propulsion by large amplitude oscillation of an airfoil with chordwise flexibility. J. Fluid Mech. 88, 485–497.CrossRefGoogle Scholar
Koochesfahani, M. M. 1989 Vortical patterns in the wake of an oscillating airfoil. AIAA J. 27 (9), 1200–1205.Google Scholar
Koumoutsakos, P. 2005 Multiscale flow simulations using particles. Annu. Rev. Fluid Mech. 37 (1), 457–487.Google Scholar
Lewin, G. C. & Haj-Hariri, H. 2003 Modelling thrust generation of a two-dimensional heaving airfoil in a viscous flow. J. Fluid Mech. 492, 339–362.Google Scholar
Lighthill, M. J. 1971 Large-amplitude elongated-body theory of fish locomotion. Proc. R. Soc. Lond. B 179, 125–138.Google Scholar
Lighthill, M. J. 1975 Mathematical Biofluiddynamics. SIAM.Google Scholar
Lu, K., Xie, Y. H. & Zhang, D. 2013 Numerical study of large amplitude, nonsinusoidal motion and camber effects on pitching airfoil propulsion. J. Fluids Struct. 36, 184–194.Google Scholar
Mackowski, A. W. & Williamson, C. H. K. 2015 Direct measurement of thrust and efficiency of an airfoil undergoing pure pitching. J. Fluid Mech. 765, 524–543.Google Scholar
Martín-Alcántara, A., Fernandez-Feria, R. & Sanmiguel-Rojas, E. 2015 Vortex flow structures and interactions for the optimum thrust efficiency of a heaving airfoil at different mean angles of attack. Phys. Fluids 27 (7), 073602.Google Scholar
Mccroskey, W. J. 1982 Unsteady airfoils. Annu. Rev. Fluid Mech. 14, 285–311.Google Scholar
Ohmi, K., Coutanceau, M., Daube, O. & Loc, T. P. 1991 Further experiments on vortex formation around an oscillating and translating airfoil at large incidences. J. Fluid Mech. 225, 607–630.Google Scholar
Quinn, D. B., Lauder, G. V. & Smits, A. J. 2015 Maximizing the efficiency of a flexible propulsor using experimental optimization. J. Fluid Mech. 767, 430–448.Google Scholar
Ramamurti, R. & Sandberg, W. 2001 Simulation of flow about flapping airfoils using finite element incompressible flow solver. AIAA J. 39 (2), 253–260.Google Scholar
Schnipper, T., Andersen, A. & Bohr, T. 2009 Vortex wakes of a flapping foil. J. Fluid Mech. 633, 411–423.Google Scholar
Shyy, W., Aono, H., Chimakurthi, S. K., Trizila, P., Kang, C.-K., Cesnik, C. E. S. & Liu, H. 2010 Recent progress in flapping wing aerodynamics and aeroelasticity. Prog. Aerosp. Sci. 46 (7), 284–327.Google Scholar
Taylor, G. K., Nudds, R. L. & Thomas, A. L. R. 2003 Flying and swimming animals cruise at a Strouhal number tuned for high power efficiency. Nature 425, 707–711.Google Scholar
Triantafyllou, M. S., Triantafyllou, G. S. & Yue, D. K. P. 2000 Hydrodynamics of fishlike swimming. Annu. Rev. Fluid Mech. 32 (1), 33–53.Google Scholar
Wang, Z. 2000 Vortex shedding and frequency selection in flapping flight. J. Fluid Mech. 410, 323–341.Google Scholar
Wu, J.-Z., Ma, H.-Y. & Zhou, M.-D. 2007 Vorticity and Vortex Dynamics. Springer.Google Scholar
Zhu, X., He, G. & Zhang, X. 2014a How flexibility affects the wake symmetry properties of a self-propelled plunging foil. J. Fluid Mech. 751, 164–183.Google Scholar
Zhu, X., He, G. & Zhang, X. 2014b Numerical study on hydrodynamic effect of flexibility in a self-propelled plunging foil. Comput. Fluids 97, 1–20.CrossRefGoogle Scholar
Supplementary material: PDF

Das supplementary material

Das supplementary material 1

Download Das supplementary material(PDF)
PDF 3.5 MB