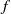Hostname: page-component-cd9895bd7-hc48f Total loading time: 0 Render date: 2024-12-28T21:46:58.770Z Has data issue: false hasContentIssue false
  • English
  • Français

Existence and properties of ageostrophic modons and coherent tripoles in the two-layer rotating shallow water model on the -plane

Published online by Cambridge University Press:  12 July 2012

Noé Lahaye  and
Vladimir Zeitlin
Noé Lahaye
Affiliation:
Laboratoire de Météorologie Dynamique/IPSL, UPMC-ENS/CNRS, 24 rue Lhomond, 75005 Paris, France
Vladimir Zeitlin*
Affiliation:
Laboratoire de Météorologie Dynamique/IPSL, UPMC-ENS/CNRS, 24 rue Lhomond, 75005 Paris, France Institut Universitaire de France
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We study formation and properties of new coherent structures: ageostrophic modons in the two-layer rotating shallow water model. The ageostrophic modons are obtained by ‘ageostrophic adjustment’ of the exact modon solutions of the two-layer quasi-geostrophic equations with the free surface, which are used to initialize the full two-layer shallow water model. Numerical simulations are performed using a well-balanced high-resolution finite volume numerical scheme. For large enough Rossby numbers, the initial configurations undergo ageostrophic adjustment towards asymmetric ageostrophic quasi-stationary coherent dipoles. This process is accompanied by substantial emission of inertia–gravity waves. The resulting dipole is shown to be robust and survives frontal collisions. It contains captured inertia–gravity waves and, for higher Rossby numbers and weak stratification, carries a (baroclinic) hydraulic jump at its axis. For stronger stratifications and high enough Rossby numbers, ‘rider’ coherent structures appear as a result of adjustment, with a monopole in one layer and a dipole in another. Other ageostrophic coherent structures, such as two-layer tripoles and two-layer modons with nonlinear scatter plot, result from the collisions of ageostrophic modons. They are shown to be long-living and robust, and to capture waves.

JFM classification

Geophysical and Geological Flows: Baroclinic flows Geophysical and Geological Flows: Rotating flows Geophysical and Geological Flows: Shallow water flows
Type
Papers
Information
Journal of Fluid Mechanics , Volume 706 , 10 September 2012 , pp. 71 - 107
Copyright
Copyright © Cambridge University Press 2012

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1. Abramowitz, M. & Stegun, I. 1964 Handbook of Mathematical Functions with Formulas, Graphs and Mathematical Tables. Dover.Google Scholar
2. Armi, L. 1986 The hydraulics of two flowing layers with different densities. J. Fluid Mech. 163, 27–58.CrossRefGoogle Scholar
3. Baey, J. M. & Carton, X. 2002 Vortex multipoles in two-layer rotating shallow-water flows. J. Fluid Mech. 460, 151–1753.CrossRefGoogle Scholar
4. Benton, G. S. 1954 The occurrence of critical flow and hydraulic jumps in a multi-layered fluid system. J. Met. 10, 139–150.2.0.CO;2>CrossRefGoogle Scholar
5. Bouchut, F. 2007 Efficient numerical finite volume schemes for shallow water models. In Nonlinear Dynamics of Rotating Shallow Water: Methods and Advances (ed. Zeitlin, V. ). Edited Series on Advances in Nonlinear Science and Complexity , vol. 2, pp. 189–256 (Chapter 4). Elsevier.CrossRefGoogle Scholar
6. Bouchut, F. & Zeitlin, V. 2010 A robust well-balanced scheme for multi-layer shallow water equations. J. Discrete Continuous Dyn. Syst. 13 (4), 739–758.CrossRefGoogle Scholar
7. Buhler, O. & McIntyre, M. E. 2005 Wave capture and wave-vortex duality. J. Fluid Mech. 534, 67–95.CrossRefGoogle Scholar
8. Carton, X. 2001 Hydrodynamical modelling of oceanic vortices. Surv. Geophys. 22, 179–263.CrossRefGoogle Scholar
9. Castro, M. J., García-Rodríguez, J. A., González-Vida, J. M., Macías, J., Parés, C. & Vázquez-Cendón, M. E. 2004 Numerical simulation of two-layer shallow water flows through channels with irregular geometry. J. Comput. Phys. 195 (1), 202–235.CrossRefGoogle Scholar
10. Couder, Y. & Basdevant, C. 1986 Experimental and numerical study of vortex couples in two-dimensional flows. J. Fluid Mech. 173, 225–251.CrossRefGoogle Scholar
11. Flierl, G. R., Larichev, V. D., McWilliams, J. C. & Reznik, G. M. 1980 The dynamics of baroclinic and barotropic solitary eddies. Dyn. Atmos. Oceans 5, 1–41.CrossRefGoogle Scholar
12. Gryanik, V. M., Sokolovskiy, M. A. & Verron, J. 2006 Dynamics of heton-like vortices. Regular Chaotic Dyn. 11 (3), 383–434.CrossRefGoogle Scholar
13. Gula, J., Zeitlin, V. & Bouchut, F. 2010 Instabilities of buoyancy-driven coastal currents and their nonlinear evolution in the two-layer rotating shallow water model. Part 2. Active lower layer. J. Fluid Mech. 665, 209–237.CrossRefGoogle Scholar
14. Haines, K. 1989 Baroclinic modons as prototypes for atmospheric blocking. J. Atmos. Sci. 46, 3202–3218.2.0.CO;2>CrossRefGoogle Scholar
15. Hesthaven, J. S., Lynov, J. P., Nielsen, A. H., Rasmussen, J. Juul, Schmidt, M. R., Shapiro, E. G. & Turitsyn, S. K. 1995 Dynamics of a nonlinear dipole vortex. Phys. Fluids 7, 2220–2229.CrossRefGoogle Scholar
16. Hogg, A. M., Dewar, W. K., Berloff, P. & Ward, M. L. 2011 Kelvin wave hydraulic control induced by interactions between vortices and topography. J. Fluid Mech. 687, 194–208.CrossRefGoogle Scholar
17. Holland, D. M., Rosales, R. R, Stefanica, D. & Tabak, E. G. 2002 Internal hydraulic jumps and mixing in two-layer flows. J. Fluid Mech. 470, 63–83.CrossRefGoogle Scholar
18. Jiang, Q. & Smith, R. B. 2001 Ideal shocks in 2-layer flow. Part 2. Under a passive layer. Tellus A 53, 146–167.CrossRefGoogle Scholar
19. Kamenkovich, V. M. & Reznik, G. M. 1978 Fizika Okeana, vol. 2, Gidrodinamika Okeana (in Russian). Nauka.Google Scholar
20. Kizner, Z. & Khvoles, R. 2004a The tripole vortex: experimental evidence and explicit solutions. Phys. Rev. E 70, 016307.CrossRefGoogle ScholarPubMed
21. Kizner, Z. & Khvoles, R. 2004b Two variations on the theme of Lamb–Chaplygin: supersmooth dipole and rotating multipoles. Regular Chaotic Dyn. 9, 509–518.CrossRefGoogle Scholar
22. Kizner, Z., Reznik, G. M., Fridman, B., Khvoles, R. & McWilliams, J. C. 2008 Shallow-water modons on the -plane. J. Fluid Mech. 603, 305–329.CrossRefGoogle Scholar
23. Klemp, J. B., Rotunno, R. & Skamarock, W. C. 1994 On the dynamics of gravity currents in a channel. J. Fluid Mech. 269, 169–198.CrossRefGoogle Scholar
24. Lahaye, N. & Zeitlin, V. 2011 Collisions of ageostrophic modons and formation of new types of coherent structures in rotating shallow water model. Phys. Fluids 23, 061703.CrossRefGoogle Scholar
25. Lahaye, N. & Zeitlin, V. 2012 Shock modon: a new type of coherent structure in rotating shallow water. Phys. Rev. Lett. 108, 044502.CrossRefGoogle ScholarPubMed
26. Larichev, V. & Reznik, G. M. 1976 Two-dimensional solitary Rossby waves. Dokl. Acad. Sci., USSR 231, 1077–1080.Google Scholar
27. Malanotte-Rizzoli, P. 1982 Planetary solitary waves in geophysical flows. Adv. Geophys. 24, 147–224.CrossRefGoogle Scholar
28. McWilliams, James C. 1980 An application of equivalent modons to atmospheric blocking. Dyn. Atmos. Oceans 5 (1), 43–66.CrossRefGoogle Scholar
29. Meleshko, V. V. & van Heijst, G. J. F. 1994 On Chaplygin’s investigations of two-dimensional vortex structures in an inviscid fluid. J. Fluid Mech. 272, 157–182.CrossRefGoogle Scholar
30. Montgomery, P. J. & Moodie, T. B. 2001 On the number of conserved quantities for the two-layer shallow-water equations. Stud. Appl. Math. 106 (2), 229–259.CrossRefGoogle Scholar
31. Pedlosky, J. 1970 Finite-amplitude baroclinic waves. J. Atmos. Sci. 27, 15–30.2.0.CO;2>CrossRefGoogle Scholar
32. Pedlosky, J. 1987 Geophysical Fluid Dynamics. Springer.CrossRefGoogle Scholar
33. Pratt, L. J. 1983 On inertial flow over topography. Part 1. Semigeostrophic adjustment to an obstacle. J. Fluid Mech. 131, 195–218.CrossRefGoogle Scholar
34. Ribstein, B., Gula, J. & Zeitlin, V. 2010 (A)geostrophic adjustment of dipolar perturbations, formation of coherent structures and their properties, as follows from high-resolution numerical simulations with rotating shallow water model. Phys. Fluids 22, 116603.CrossRefGoogle Scholar
35. Schar, C. & Smith, R. B. 1993 Shallow-water flow past isolated topography. Part 1. Vorticity production and wake formation. J. Atmos. Sci. 50 (10), 1373–1400.2.0.CO;2>CrossRefGoogle Scholar
36. Snyder, C., Muraki, D. J., Plougonven, R. & Zhang, F. 2007 Inertia-gravity waves generated within a dipole vortex. J. Atmos. Sci. 64 (12), 4417–4431.CrossRefGoogle Scholar
37. van Heijst, G. J. F. & Flor, J. B. 1989 Dipole formation and collisions in a stratified fluid. Nature 340, 212–215.CrossRefGoogle Scholar
38. van Heijst, G. J. F. & Kloosterziel, R. C. 1989 Tripolar vortices in a rotating fluid. Nature 338, 569–571.CrossRefGoogle Scholar
39. Verron, J. & Sokolovskiy, M. A. 2002 Dynamics of triangular two-layer vortex structures with zero total intensity. Regular Chaotic Dyn. 7 (4), 435–472.Google Scholar
40. Yih, S. & Guha, C. R. 1955 Hydraulic jump in a fluid system of two layers. Tellus 7, 358–366.CrossRefGoogle Scholar