Hostname: page-component-586b7cd67f-rdxmf Total loading time: 0 Render date: 2024-11-23T05:41:38.089Z Has data issue: false hasContentIssue false
  • English
  • Français

Exact two-dimensionalization of rapidly rotating large-Reynolds-number flows

Published online by Cambridge University Press:  22 October 2015

Basile Gallet
Basile Gallet*
Affiliation:
Service de Physique de l’État Condensé, CEA, CNRS UMR 3680, Université Paris-Saclay, CEA Saclay, 91191 Gif-sur-Yvette, France
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We consider the flow of a Newtonian fluid in a three-dimensional domain, rotating about a vertical axis and driven by a vertically invariant horizontal body force. This system admits vertically invariant solutions that satisfy the 2D Navier–Stokes equation. At high Reynolds number and without global rotation, such solutions are usually unstable to three-dimensional perturbations. By contrast, for strong enough global rotation, we prove rigorously that the 2D (and possibly turbulent) solutions are stable to vertically dependent perturbations. We first consider the 3D rotating Navier–Stokes equation linearized around a statistically steady 2D flow solution. We show that this base flow is linearly stable to vertically dependent perturbations when the global rotation is fast enough: under a Reynolds-number-dependent threshold value 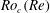$Ro_{c}(Re)$ of the Rossby number, the flow becomes exactly 2D in the long-time limit, provided that the initial 3D perturbations are small. We call this property linear two-dimensionalization. We compute explicit lower bounds on 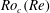$Ro_{c}(Re)$ and therefore determine regions of the parameter space 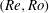$(Re,Ro)$ where such exact two-dimensionalization takes place. We present similar results in terms of the forcing strength instead of the root-mean-square velocity: the global attractor of the 2D Navier–Stokes equation is linearly stable to vertically dependent perturbations when the forcing-based Rossby number 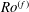$Ro^{(f)}$ is lower than a Grashof-number-dependent threshold value 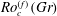$Ro_{c}^{(f)}(Gr)$. We then consider the fully nonlinear 3D rotating Navier–Stokes equation and prove absolute two-dimensionalization: we show that, below some threshold value 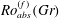$Ro_{\mathit{abs}}^{(f)}(Gr)$ of the forcing-based Rossby number, the flow becomes two-dimensional in the long-time limit, regardless of the initial condition (including initial 3D perturbations of arbitrarily large amplitude). These results shed some light on several fundamental questions of rotating turbulence: for arbitrary Reynolds number 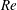$Re$ and small enough Rossby number, the system is attracted towards purely 2D flow solutions, which display no energy dissipation anomaly and no cyclone–anticyclone asymmetry. Finally, these results challenge the applicability of wave turbulence theory to describe stationary rotating turbulence in bounded domains.

JFM classification

Geophysical and Geological Flows: Rotating flows Turbulent Flows: Rotating turbulence Geophysical and Geological Flows: Waves in rotating fluids
Type
Papers
Information
Journal of Fluid Mechanics , Volume 783 , 25 November 2015 , pp. 412 - 447
Check for updates
Copyright
© 2015 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Alexakis, A. 2015 Rotating Taylor–Green flow. J. Fluid Mech. 769, 46–78.CrossRefGoogle Scholar
Alexakis, A. & Doering, C. R. 2006 Energy and enstrophy dissipation in steady state 2d turbulence. Phys. Lett. A 359, 652–657.Google Scholar
Babin, A., Mahalov, A. & Nicolaenko, B. 1997 Regularity and integrability of 3D Euler and Navier–Stokes equations for rotating fluids. Asymptot. Anal. 15, 103–150.Google Scholar
Babin, A., Mahalov, A. & Nicolaenko, B. 2000 Global regularity of 3D rotating Navier–Stokes equations for resonant domains. Appl. Math. Lett. 13 (4), 51–57.CrossRefGoogle Scholar
Baroud, C. N., Plapp, B. B., Swinney, H. L. & She, Z.-S. 2003 Scaling in three-dimensional and quasi-two-dimensional rotating turbulent flows. Phys. Fluids 15 (8), 2091.Google Scholar
Bartello, P., Métais, O. & Lesieur, M. 1994 Coherent structures in rotating three-dimensional turbulence. J. Fluid Mech. 273, 1.Google Scholar
Boffetta, G., Celani, A. & Vergassola, M. 2000 Inverse energy cascade in two-dimensional turbulence: deviations from Gaussian behavior. Phys. Rev. E 61, 1.Google Scholar
Bourouiba, L. & Bartello, P. 2007 The intermediate Rossby number range and two-dimensional–three-dimensional transfers in rotating decaying homogeneous turbulence. J. Fluid Mech. 587, 139.Google Scholar
Cambon, C. & Jacquin, L. 1989 Spectral approach to non-isotropic turbulence subjected to rotation. J. Fluid Mech. 202, 295–317.CrossRefGoogle Scholar
Cambon, C., Rubinstein, R. & Godeferd, F. S. 2004 Advances in wave turbulence: rapidly rotating flows. New J. Phys. 6, 73.Google Scholar
Campagne, A., Gallet, B., Moisy, F. & Cortet, P.-P. 2014 Direct and inverse energy cascades in a forced rotating turbulence experiment. Phys. Fluids 26, 125112.Google Scholar
Campagne, A., Gallet, B., Moisy, F. & Cortet, P.-P. 2015 Disentangling inertial waves from eddy turbulence in a forced rotating turbulence experiment. Phys. Rev. E 91, 043016.Google Scholar
Constantin, P., Foias, C. & Manley, O. P. 1994 Effects of the forcing function spectrum on the energy spectrum in 2-D turbulence. Phys. Fluids 6, 427.Google Scholar
Davidson, P. A. 2013 Turbulence in Rotating, Stratified and Electrically Conducting Fluids. Cambridge University Press.CrossRefGoogle Scholar
Deusebio, E., Boffetta, G., Lindborg, E. & Musacchio, S. 2014 Dimensional transition in rotating turbulence. Phys. Rev. E 90, 023005.Google Scholar
Doering, C. R. & Foias, C. 2002 Energy dissipation in body-forced turbulence. J. Fluid Mech. 467, 289–306.Google Scholar
Frisch, U. 1995 Turbulence: The Legacy of A.N. Kolmogorov. Cambridge University Press.Google Scholar
Gallet, B., Campagne, A., Cortet, P.-P. & Moisy, F. 2014 Scale-dependent cyclone–anticyclone asymmetry in a forced rotating turbulence experiment. Phys. Fluids 26, 035108.CrossRefGoogle Scholar
Gallet, B. & Doering, C. R. 2015 Exact two-dimensionalization of low-magnetic-Reynolds-number flows subject to a strong magnetic field. J. Fluid Mech. 773, 154–177.Google Scholar
Galtier, S. 2003 Weak inertial-wave turbulence theory. Phys. Rev. E 68, 015301.Google Scholar
Greenspan, H. P. 1990 The Theory of Rotating Fluids. Breukelen.Google Scholar
Ladyzhenskaya, O. A. 1963 The Mathematical Theory of Viscous Incompressible Flow. Gordon and Breach.Google Scholar
Mininni, P. D., Alexakis, A. & Pouquet, A. 2009 Scale interactions and scaling laws in rotating flows at moderate Rossby numbers and large Reynolds numbers. Phys. Fluids 21, 015108.CrossRefGoogle Scholar
Morize, C., Moisy, F. & Rabaud, M. 2005 Decaying grid-generated turbulence in a rotating tank. Phys. Fluids 17 (9), 095105.Google Scholar
Moisy, F., Morize, C., Rabaud, M. & Sommeria, J. 2011 Decay laws, anisotropy and cyclone–anticyclone asymmetry in decaying rotating turbulence. J. Fluid Mech. 666, 5.Google Scholar
Müller, W. C. & Thiele, M. 2007 Scaling and energy transfer in rotating turbulence. Europhys. Lett. 77, 3.CrossRefGoogle Scholar
Naso, A. 2015 Cyclone–anticyclone asymmetry and alignment statistics in homogeneous rotating turbulence. Phys. Fluids 27, 035108.Google Scholar
Paret, J. & Tabeling, P. 1998 Intermittency in the two-dimensional inverse cascade of energy: experimental observations. Phys. Fluids 10, 3126.CrossRefGoogle Scholar
Sagaut, P. & Cambon, C. 2008 Homogeneous Turbulence. Cambridge University Press.Google Scholar
Scott, J. F. 2015 Wave turbulence in a rotating channel. J. Fluid Mech. 741, 316–349.Google Scholar
Seiwert, J., Morize, C. & Moisy, F. 2008 On the decrease of intermittency in decaying rotating turbulence. Phys. Fluids 20, 071702.CrossRefGoogle Scholar
Smith, L. M., Chasnov, J. R. & Waleffe, F. 1996 Crossover from two- to three-dimensional turbulence. Phys. Rev. Lett. 77, 2467.Google Scholar
Smith, L. M. & Waleffe, F. 1999 Transfer of energy to two-dimensional large scales in forced, rotating three-dimensional turbulence. Phys. Fluids 11, 6.CrossRefGoogle Scholar
Sreenivasan, B. & Davidson, P. A. 2008 On the formation of cyclones and anticyclones in a rotating fluid. Phys. Fluids 20, 085104.CrossRefGoogle Scholar
Vanneste, J. 2013 Balance and spontaneous wave generation in geophysical flows. Annu. Rev. Fluid Mech. 45, 147–172.Google Scholar
Waleffe, F. 1993 Inertial transfers in the helical decomposition. Phys. Fluids A 5, 677.Google Scholar
Yarom, E. & Sharon, E. 2014 Experimental observation of steady inertial wave turbulence in deep rotating flows. Nat. Phys. 10, 510–514.Google Scholar