Hostname: page-component-586b7cd67f-2brh9 Total loading time: 0 Render date: 2024-11-22T14:27:33.096Z Has data issue: false hasContentIssue false
  • English
  • Français

Exact solutions for quasi-one-dimensional compressible viscous flows in conical nozzles

Published online by Cambridge University Press:  08 March 2021

Alessandro Ferrari Open the ORCID record for Alessandro Ferrari [Opens in a new window]
Alessandro Ferrari*
Affiliation:
Energy Department, Politecnico di Torino, Corso Duca degli Abruzzi 24, Torino10129, Italy
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

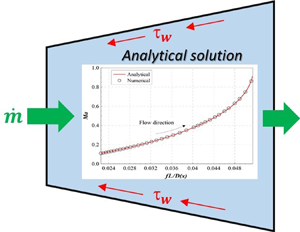
New analytical solutions for the one-dimensional steady-state compressible viscous adiabatic flow of an ideal gas through a conical nozzle or diffuser have been obtained. In order to analytically solve the problem, it is essential to determine the correct transformations of the variables and to identify the kinetic energy per unit of mass as the physical variable that appears in the final Abel ordinary differential equation.

A dimensionless representation is given of the new solution, which points out the fundamental role exerted by some dimensionless groups in problems where viscous power dissipation and variable flow areas are present simultaneously as driving factors of flow changes. Furthermore, a steady-state fluid dynamics analysis of the compressible viscous flows in conical nozzles and diffusers has been carried out to improve the physical interpretation of the solutions.

Finally, the thus determined analytical solutions have been validated for both subsonic and supersonic flows through a comparison with numerical solutions pertaining to the same ordinary differential equation. However, when the exact solution includes shocks, the time-asymptotic numerical solutions of the Euler equations for the quasi-one-dimensional unsteady-state gas dynamics are used for validation and the discretisation is performed by applying a finite volume technique.

The proposed analytical solutions are complementary to the Fanno and nozzle models that refer to a viscous adiabatic constant cross-section pipe flow and an inviscid adiabatic variable cross-section pipe flow, respectively, and extend the collection of the exact solutions of gas dynamics.

JFM classification

Aerodynamics: High-speed flow Compressible Flows: Gas dynamics Mathematical Foundations: General fluid mechanics
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 915 , 25 May 2021 , A1
Check for updates
Copyright
© The Author(s), 2021. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Anderson, J.D. 1995 Computational Fluid Dynamics. McGraw-Hill Inc.Google Scholar
Anderson, J. 2003 Modern Compressible Flow with Historical Perspective. McGraw-Hill.Google Scholar
Asako, Y., Pi, T., Turner, S.E. & Faghri, M. 2003 Effect of compressibility on gaseous flows in micro-channels. Intl J. Heat Mass Transfer 46 (16), 3041–3050.CrossRefGoogle Scholar
Atmaca, A.U., Erek, A. & Ekren, O. 2020 One-dimensional analysis of the convergent-divergent motive nozzle for the two-phase ejector: effect of the operating and design parameters. Appl. Therm. Engng 181, article 155866.CrossRefGoogle Scholar
Bejan, A. 2013 Convection Heat Transfer, 4th edn. John Wiley & Sons.CrossRefGoogle Scholar
Bermudez, A., Lopez, X. & Vasquez-Cendon, M.E. 2017 Finite volume methods for multi-component Euler equations with source terms. Comput. Fluids 156, 113–134.CrossRefGoogle Scholar
Bogouffa, L. 2010 New exact general solutions of Abel equation of the second kind. Appl. Maths Comput. 216 (2), 689–691.CrossRefGoogle Scholar
Bogouffa, L. 2014 Further solutions of the general Abel equation of the second kind: use of Julia's condition. Appl. Maths 14, 53–56.Google Scholar
Butcher, J.C. 2016 Numerical Methods for Ordinary Differential Equations, 3rd edn. John Wiley & Sons.CrossRefGoogle Scholar
Cavazzuti, M. & Corticelli, M. 2017 Numerical modelling of Fanno flows in micro-channels: a quasi-static application to air vents for plastic moulding. Therm. Sci. Engng Prog. 2, 43–56.CrossRefGoogle Scholar
Cavazzuti, M., Corticelli, M. & Karayiannis, T.G. 2019 Compressible Fanno flows in micro-channels: an enhanced quasi-2D numerical model for laminar flows. Therm. Sci. Engng Prog. 10, 10–26.CrossRefGoogle Scholar
Cheng, N.S. 2008 Formulas for friction factor in transitional regions. ASCE J. Hydraul. Engng 134 (9), 1357–1362.CrossRefGoogle Scholar
Douglas, J.F., Gasiorek, J.M., Swaffield, J.A. & Jack, L.B. 2005 Fluid Mechanics, 5th edn. Pearson Prentice Hall.Google Scholar
Emmanuelli, A., Zheng, J., Huet, M., Giauque, A., Le Garrec, T. & Ducruix, S. 2020 Description and application of a 2D-axisymmetric model for entropy noise in nozzle flows. J. Sound Vib. 472, 115163.CrossRefGoogle Scholar
Emmons, H.W. 1958 Fundamentals of Gas Dynamics. Princeton University Press.CrossRefGoogle Scholar
Ferrari, A. 2020 Exact solutions for 1-D compressible diabatic flows with wall friction.J. Fluid Mech. (submitted to).Google Scholar
Hairer, E., Norsett, S.P. & Wanner, G. 1993 Solving Ordinary Differential Equations I. Nonstiff Problems, 2nd edn. Springer-Verlag.Google Scholar
Hasselmann, K., der Wiesche, S. & Kenig, E.Y. 2019 Optimization of piecewise conical nozzles: theory and application. Trans. ASME J. Fluids Engng 141, article no. 121202.CrossRefGoogle Scholar
Hirsch, C. 2007 Numerical Computation of Internal and External Flows. Butterworth-Heinemann.Google Scholar
Hong, C., Nakamura, T., Asako, Y. & Ueno, I. 2016 Semi-local friction factor of turbulent gas flow through rectangular microchannels. Intl J. Heat Mass Transfer 98, 643–649.CrossRefGoogle Scholar
Kamke, E. 1983 Losugmethoden und losungen. Teubner.Google Scholar
Kamm, R.D. & Shapiro, A.H. 1979 Unsteady flow in a collapsible tube subjected external pressure or body forces. J. Fluid Mech. 95, 1–78.CrossRefGoogle Scholar
Kirkland, W.M. 2019 A polytropic approximation of compressible flow in pipes with friction. ASME Transactions, Trans. ASME J. Fluids Engng 141 (12), article no. 121404.Google Scholar
Kohl, M.J., Abdel-Khalik, S.I., Jeter, S.M. & Sadowski, D.L. 2005 An experimental investigation of microchannel flow with internal pressure measurements. Intl J. Heat Mass Transfer 48, 1518–1533.CrossRefGoogle Scholar
Loh, W.H.T. 1970 A generalized one-dimensional compressible flow analysis with heat addition and/or friction in a non-constant area duct. Intl J. Engng Sci. 8 (3), 193–206.CrossRefGoogle Scholar
Maeda, K. & Colonius, T. 2017 A source term approach for generation of one-way acoustic waves in the Euler and Navier–Stokes equations. Wave Motion 75, 36–49.CrossRefGoogle ScholarPubMed
Mahapatra, S., Nelaturi, A., Tennyson, J.A. & Ghosh, S. 2019 Large eddy simulation of compressible turbulent flow in convergent-divergent nozzles with isothermal wall. Intl J. Heat Fluid Flow 78, article 108425.CrossRefGoogle Scholar
Maicke, B.A. & Bondarev, G. 2017 Quasi-one-dimensional modelling of pressure effects in supersonic nozzles. Aerosp. Sci. Technol. 70, 161–169.CrossRefGoogle Scholar
Maicke, B.A. & Majdalani, J. 2012 Inversion of the fundamental thermodynamic equations for isen-tropic nozzle flow analysis. Trans. ASME: J. Engng Gas Turbines Power 134, 031201.Google Scholar
Mak, M. & Harko, T. 2002 New method for generating general solution of the Abel differential equation. Comput. Maths Applics. 43, 91–94.CrossRefGoogle Scholar
Markakis, M.P. 2009 Closed-form solutions of certain Abel equations of the first kind. Appl. Maths Lett. 22, 1401–1405.CrossRefGoogle Scholar
Martelli, E., Saccoccio, L., Ciottoli, P.P., Tinney, C.E., Baars, W.J. & Bernardini, M. 2020 Flow dynamics and wall-pressure signatures in a high-Reynolds-number overexpanded nozzle with free shock separation. J. Fluid Mech. 895, A29.CrossRefGoogle Scholar
Moran, M.J., Shapiro, H.N., Boettner, D.D. & Bailey, M. 2010 Fundamentals of Engineering Thermodynamics, 7th edn. John Wiley & Sons.Google Scholar
Panayotounakos, D.E. 2005 Exact analytic solutions of unsolvable classes of first and second order nonlinear ODEs (part I: Abel's equation). Appl. Maths Lett. 18, 155–162.CrossRefGoogle Scholar
Parker, G.J. 1989 Adiabatic compressible flow in parallel ducts: an approximate but rapid method of solution. Intl. J. Fluid Flow 10 (2), 179–181.CrossRefGoogle Scholar
Polyanin, A.D. & Zaitsev, V.F. 2003 Handbook of Exact Solutions for Ordinary Differential Equations, 2nd edn. Chapman & Hall/CRC.Google Scholar
Prud'homme, R. 2010 Flows of Reactive Fluids. Springer.CrossRefGoogle Scholar
Rodriguez Lastra, M., Fernandez Oro, J.M., Vega Galdo, M., Marigorta Blanco, E. & Morros Santolaria, C. 2013 J. Wind Engng Ind. Aerodyn. 118, 35–43.CrossRefGoogle Scholar
Schwartz, L.W. 1987 A perturbation solution for compressible viscos channel flows. J. Engng Maths 21 (1), 69–86.CrossRefGoogle Scholar
Senftle, F., Michael, A., Thorpe, A.N., James, C. & Grant, J.R. 2003 Viscous gas through a nozzle treated as an exponential function. Exp. Therm. Fluid Sci. 27, 261–269.CrossRefGoogle Scholar
Shapiro, A. 1953 The Dynamics and Thermodynamics of Compressible Fluid Flow, vol. 1. John Wiley & Sons.Google Scholar
Shiraishi, T., Murayama, E., Kawakami, Y. & Nakano, K. 2011 Approximate solution of pneumatic steady-state characteristics in tubes with friction. In Proceedings of the 8th JFPS Symposium on Fluid Power, Okinawa, October 25–28, pp. 242–247.Google Scholar
Sutton, G.P. 1992 Rocket Propulsion Elements, 6th edn. Wiley.Google Scholar
Toro, E. 2009 Riemann Solvers and Numerical Methods for Fluid Dynamics. Springer-Verlag.CrossRefGoogle Scholar
Urata, E. 2013 A flow-rate equation for subsonic Fanno flow. Proc. Inst. Mech. Engrs. C 227 (12), 2724–2729.Google Scholar
White, F.M. 2015 Fluid Mechanics, 8th edn. McGrawHill.Google Scholar
Yarin, L.P. 2012 The Pi-theorem - Applications to Fluid Mechanics and Heat and Mass Transfer. Springer-Verlag.Google Scholar
Yu, K., Chen, Y., Huang, S., Lv, Z. & Xu, J. 2020 Optimization and analysis of inverse design method of maximum thrust scramjet nozzles. Aerosp. Sci. Technol. 105, article no. 105948.CrossRefGoogle Scholar
Zaman, K.B.M.Q., Dahl, M.D., Bencic, T.J. & Loh, C.Y. 2002 Investigation of a ‘transonic resonance’ with convergent divergent nozzles. J. Fluid Mech. 463, 313–343.CrossRefGoogle Scholar