Hostname: page-component-cd9895bd7-dzt6s Total loading time: 0 Render date: 2024-12-24T00:33:22.545Z Has data issue: false hasContentIssue false
  • English
  • Français

Evolution of elliptic synthetic jets at low Reynolds number

Published online by Cambridge University Press:  08 April 2019

Xu-Dong Shi Open the ORCID record for Xu-Dong Shi [Opens in a new window] ,
Li-Hao Feng Open the ORCID record for Li-Hao Feng [Opens in a new window]  and
Jin-Jun Wang Open the ORCID record for Jin-Jun Wang [Opens in a new window]
Xu-Dong Shi
Affiliation:
Fluid Mechanics Key Laboratory of Education Ministry, Beijing University of Aeronautics and Astronautics, Beijing 100191, PR China
Li-Hao Feng*
Affiliation:
Fluid Mechanics Key Laboratory of Education Ministry, Beijing University of Aeronautics and Astronautics, Beijing 100191, PR China
Jin-Jun Wang
Affiliation:
Fluid Mechanics Key Laboratory of Education Ministry, Beijing University of Aeronautics and Astronautics, Beijing 100191, PR China
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

The influence of the nozzle aspect ratio (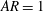$AR=1$, 2 and 4), stroke length (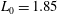$L_{0}=1.85$, 3.7 and 5.55) and Reynolds number (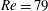$Re=79$, 158, 316 and 632) on the behaviour of elliptic synthetic jets is studied experimentally. Laser-induced fluorescence and two-dimensional and stereoscopic particle image velocimetry are used to analyse the vortex dynamics and evolution mechanism. It is found that the fluid elements around the major axis of an elliptic vortex ring move downstream faster and tend to approach the centreline, while the fluid elements around the minor axis move downstream at a slower speed and away from the centreline, thereby resulting in the occurrence of the well-known axis-switching phenomenon for elliptic synthetic jets. During this process, a pair of arc-like vortices forms ahead of the primary vortex ring, and they are constituted by streamwise vortices in the leg part and spanwise vortices in the head part; two pairs of streamwise vortices form from the inside of the primary vortex ring and develop in the tails. The streamwise vortices are pushed away progressively from the centreline by the synthetic jet vortex rings that are formed during the subsequent periods. These additional vortical structures for non-circular synthetic jets show regular and periodic characteristics, which are quite different from the previous findings for non-circular jets. Their mutual interaction with the vortex ring causes significant changes in the topology of elliptic synthetic jets, which further results in the variation of the statistical characteristics. Increasing the aspect ratio, stroke length and Reynolds number will make the evolution of the synthetic jet become more unstable and complex. In addition, the entrainment rate of an elliptical synthetic jet is larger than that of a circular synthetic jet and it increases with the nozzle aspect ratio (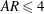$AR\leqslant 4$) and Reynolds number. It is indicated that the formation of streamwise vortices could enhance the entrainment rate. This finding provides substantial evidence for the potential application of elliptic synthetic jets for effective flow control.

JFM classification

Wakes/Jets: Jets Vortex Flows: Vortex dynamics Vortex Flows: Vortex instability
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 868 , 10 June 2019 , pp. 66 - 96
Copyright
© 2019 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Abdou, S. & Ziada, S. 2006 Spanwise characteristics of high-aspect-ratio synthetic jet. AIAA J. 44 (7), 1516–1523.Google Scholar
Austin, T. R.1993 The small scale topology of a 2 : 1 aspect-ratio elliptic jet. PhD thesis, University of Southern California, Los Angeles.Google Scholar
Batchelor, G. K. 1967 An Introduction to Fluid Mechanics. Cambridge University Press.Google Scholar
Brancher, P., Chomaz, J. M. & Huerre, P. 1994 Direct numerical simulations of round jets: vortex induction and side jets. Phys. Fluids 6 (5), 1768–1774.Google Scholar
Cantwell, B. & Coles, D. 1983 An experimental study of entrainment and transport in the turbulent near wake of a circular cylinder. J. Fluid Mech. 136, 321–374.Google Scholar
Champagnat, F., Plyer, A., Le Besnerais, G., Leclaire, B., Davoust, S. & Le Sant, Y. 2011 Fast and accurate PIV computation using highly parallel iterative correlation maximization. Exp. Fluids 50 (4), 1169–1182.Google Scholar
Cater, J. E. & Soria, J. 2002 The evolution of round zero-net-mass-flux jets. J. Fluid Mech. 472, 167–200.Google Scholar
Dennis, D. J. C. & Nickels, T. B. 2008 On the limitations of Taylor’s hypothesis in constructing long structures in a turbulent boundary layer. J. Fluid Mech. 614, 197–206.Google Scholar
Di Cicca, G. M. & Iuso, G. 2007 On the near field of an axisymmetric synthetic jet. Fluid Dyn. Res. 39 (9–10), 673–693.Google Scholar
Duan, T. & Wang, J. J. 2016 Experimental investigation on the evolution of axi-symmetrical synthetic jet. J. Vis. 19 (3), 351–358.Google Scholar
Feng, L. H. & Wang, J. J. 2010 Circular cylinder vortex-synchronization control with a synthetic jet positioned at the rear stagnation point. J. Fluid Mech. 662, 232–259.Google Scholar
Gharib, M., Rambod, E. & Shariff, K. 1998 A universal time scale for vortex ring formation. J. Fluid Mech. 360, 121–140.Google Scholar
Glezer, A. & Amitay, M. 2002 Synthetic jet. Annu. Rev. Fluid Mech. 34, 503–529.Google Scholar
Green, M. A., Rowley, C. W. & Haller, G. 2007 Detection of Lagrangian coherent structures in three-dimensional turbulence. J. Fluid Mech. 572, 111–120.Google Scholar
Grinstein, F. F. 1995 Self-induced vortex ring dynamics in subsonic rectangular jets. Phys. Fluids 7 (10), 2519–2521.Google Scholar
Grinstein, F. F. 2001 Vortex dynamics and entrainment in rectangular free jets. J. Fluid Mech. 437, 69–101.Google Scholar
Grinstein, F. F. & Devore, C. R. 1996 Dynamics of coherent structures and transition to turbulence in free square jets. Phys. Fluids 8 (5), 1237–1251.Google Scholar
Gutmark, E. J. & Grinstein, F. F. 1999 Flow control with noncircular jets. Annu. Rev. Fluid Mech. 31, 239–272.Google Scholar
Haller, G. 2015 Lagrangian coherent structures. Annu. Rev. Fluid Mech. 47, 137–162.Google Scholar
Hashiehbaf, A. & Romano, G. P. 2014 Experimental investigation on circular and non-circular synthetic jets issuing from sharp edge orifices. In 17th International Symposium on Applications of Laser Techniques to Fluid Mechanics, Lisbon, Portugal, 7–10 July, 2014, pp. 56–65.Google Scholar
Hunt, J. C. R., Wray, A. A. & Moin, P. 1988 Eddies, streams, and convergence zones in turbulent flows. Proceedings of the Summer Program, Center for Turbulence Research, pp. 193–208. CTR.Google Scholar
Hussain, F. & Husain, H. S. 1989 Elliptic jets. Part 1. Characteristics of unexcited and excited jets. J. Fluid Mech. 208, 257–320.Google Scholar
Husain, H. S. & Hussain, F. 1993 Elliptic jets. Part 3. Dynamics of preferred mode coherent structure. J. Fluid Mech. 248, 315–361.Google Scholar
Kotapati, R. B., Mittal, R. & Cattafesta, L. N. III 2007 Numerical study of a transitional synthetic jet in quiescent external flow. J. Fluid Mech. 581, 287–321.Google Scholar
Krishnan, G. & Mohseni, K. 2009 Axisymmetric synthetic jets: an experimental and theoretical examination. AIAA J. 47 (10), 2273–2283.Google Scholar
Lawson, J. M. & Dawson, J. R. 2013 The formation of turbulent vortex rings by synthetic jets. Phys. Fluids 25 (10), 105113.Google Scholar
Liepmann, D. & Gharib, M. 1992 The role of streamwise vorticity in the near-field entrainment of round jets. J. Fluid Mech. 245, 643–668.Google Scholar
Maxworthy, T. 1972 The structure and stability of vortex rings. J. Fluid Mech. 51 (1), 15–32.Google Scholar
Mohseni, K., Ran, H. & Colonius, T. 2001 Numerical experiments on vortex ring formation. J. Fluid Mech. 430, 267–282.Google Scholar
Naitoh, T., Fukuda, N., Gotoh, T., Yamada, H. & Nakajima, K. 2002 Experimental study of axial flow in a vortex ring. Phys. Fluids 14 (1), 143–149.Google Scholar
O’Farrell, C. & Dabiri, J. O. 2014 Pinch-off of non-axisymmetric vortex rings. J. Fluid Mech. 740, 61–96.Google Scholar
Oren, L., Gutmark, E., Muragappan, S. & Khosla, S.2009 Flow characteristics of non circular synthetic jets. AIAA Paper 2009-1309.Google Scholar
Oren, L., Gutmark, E., Muragappan, S. & Khosla, S.2010 Turbulence characteristics of axisymmetric and non-circular synthetic jets. AIAA Paper 2010-1261.Google Scholar
Oshima, y., Izutsu, N., Oshima, K. & Hussain, A. K. M. F. 1988 Bifurcation of an elliptic vortex ring. Fluid Dyn. Res. 3, 133–139.Google Scholar
Pan, C., Wang, H. P. & Wang, J. J. 2013 Phase identification of quasi-periodic flow measured by particle image velocimetry with a low sampling rate. Meas. Sci. Technol. 24, 055305.Google Scholar
Pan, C., Xue, D., Xu, Y., Wang, J. J. & Wei, R. J. 2015 Evaluating the accuracy performance of Lucas-Kanade algorithm in the circumstance of PIV application. Sci. China Phys. Mech. Astron. 58 (10), 104704.Google Scholar
Quinn, W. R. 2007 Experimental study of the near field and transition region of a free jet issuing from a sharp-edged elliptic nozzle plate. Eur. J. Mech. (B/Fluids) 26 (4), 583–614.Google Scholar
Raffel, M., Willert, C. E., Wereley, S. T. & Kompenhans, J. 2007 Particle Image Velocimetry: A Practical Guide. Springer.Google Scholar
Ravi, B. R., Mittal, R. & Najjar, F. M.2004 Study of three-dimensional synthetic jet flowfields using direct numerical simulation. AIAA Paper 2004-0091.Google Scholar
Ravi, B. R. & Mittal, R.2006 Numerical study of large aspect-ratio synthetic jets. AIAA Paper 2006-0315.Google Scholar
Scarano, F. & Riethmuller, M. L. 1999 Iterative multigrid approach in PIV image processing with discrete window offset. Exp. Fluids 26 (6), 513–523.Google Scholar
Shan, R. Q. & Wang, J. J. 2010 Experimental studies of the influence of parameters on axisymmetric synthetic jets. Sensors Actuators A 157 (1), 107–112.Google Scholar
Sahni, O., Wood, J., Jansen, K. E. & Amitay, M. 2011 Three-dimensional interactions between a finite-span synthetic jet and cross-flow. J. Fluid Mech. 671, 254–287.Google Scholar
Shuster, J. M. & Smith, D. R. 2007 Experimental study of the formation and scaling of a round synthetic jet. Phys. Fluids 19 (4), 045109.Google Scholar
Smith, B. L. & Swift, G. W. 2003 A comparison between synthetic jets and continuous jets. Exp. Fluids 34 (4), 467–472.Google Scholar
Smith, B. L. & Glezer, A. 1998 The formation and evolution of synthetic jet. Phys. Fluids 10 (9), 2281–2297.Google Scholar
Sung, J. & Yoo, J. Y. 2003 Near-wake vortex motions behind a circular cylinder at low Reynolds number. J. Fluids Struct. 17 (2), 261–274.Google Scholar
Tang, H. & Zhong, S.2005 Modelling of the characteristics of synthetic jet actuators. AIAA Paper 2005-4748.Google Scholar
Tang, H. & Zhong, S. 2015 Simulation and modeling of synthetic jets. Vortex Rings and Jets: Recent Developments in Near-Field Dynamics, pp. 93–144. Springer.Google Scholar
Toyoda, K. & Hiramoto, R. 2009 Manipulation of vortex rings for flow control. Fluid Dyn. Res. 41 (5), 051402.Google Scholar
Toyoda, K. & Mori, H. 2001 Three-dimensional vortical structure and mixing mechanism of a circular jet. J. Vis. 4 (3), 239–244.Google Scholar
Xia, Q. & Zhong, S. 2012 A PLIF and PIV study of liquid mixing enhanced by a lateral synthetic jet pair. Intl J. Heat Fluid Flow 37, 64–73.Google Scholar
Yamada, H. & Matsui, T. 1979 Mutual slip-through of a pair of vortex rings. Phys. Fluids 22 (7), 1245–1249.Google Scholar
Zawadzki, I. & Aref, H. 1991 Mixing during vortex ring collision. Phys. Fluids A 3 (5), 1405–1410.Google Scholar
Zhang, H., Chen, Z., Li, B. & Jiang, X. 2014 The secondary vortex rings of a supersonic underexpanded circular jet with low pressure ratio. Eur. J. Mech. (B/Fluids) 46, 172–180.Google Scholar
Zhang, P. F., Wang, J. J. & Feng, L. H. 2008 Review of zero-net-mass-flux jet and its application in separation flow control. Sci. China Ser. E 51 (9), 1315–1344.Google Scholar
Zhong, S., Jabbal, M., Tang, H., Garcillan, L., Guo, F., Wood, N. & Warsop, C. 2007 Towards the design of synthetic-jet actuators for full-scale flight conditions. Part 1: The fluid mechanics of synthetic-jet actuators. Flow Turbul. Combust. 78 (3–4), 283–307.Google Scholar
Zhong, S. & Zhang, S. 2013 Further examination of the mechanism of round synthetic jets in delaying turbulent flow separation. Flow Turbul. Combust. 91 (1), 177–208.Google Scholar
Zhou, J., Tang, H. & Zhong, S. 2009 Vortex roll-up criterion for synthetic jets. AIAA J. 47 (5), 1252–1262.Google Scholar