Hostname: page-component-78c5997874-fbnjt Total loading time: 0 Render date: 2024-11-04T21:48:21.351Z Has data issue: false hasContentIssue false
  • English
  • Français

Evolution of a stratified rotating shear layer with horizontal shear. Part 2. Nonlinear evolution

Published online by Cambridge University Press:  06 September 2013

Eric Arobone  and
Sutanu Sarkar
Eric Arobone
Affiliation:
Department of Mechanical and Aerospace Engineering, University of California San Diego, CA 92093, USA
Sutanu Sarkar*
Affiliation:
Department of Mechanical and Aerospace Engineering, University of California San Diego, CA 92093, USA
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Direct numerical simulation is used to investigate the nonlinear evolution of a horizontally oriented mixing layer with uniform stable stratification and coordinate system rotation about the vertical axis. The important dimensional parameters governing inviscid dynamics are maximum shear 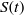$S(t)$, buoyancy frequency 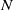$N$, angular velocity of rotation 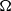$\Omega $ and characteristic shear thickness 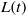$L(t)$. The effect of rotation rate, 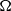$\Omega $, on the development of fluctuations in the shear layer is systematically studied in a regime of strong stratification. An instability mechanism, qualitatively distinct from the inertial instability, is found to deform columnar vortex cores in vertical planes for a strongly stratified rotating mixing layer. This mechanism emerges when centreline absolute vertical vorticity, 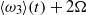$\langle {\omega }_{3} \rangle (t)+ 2\Omega $, is nearly zero as predicted by the linear stability analysis in Part 1 (J. Fluid. Mech., vol. 703, 2012, pp. 29–48). When the initial rotation rate is moderately anticyclonic, strong destabilization and a cascade to small scales is observed, consistent with prior studies involving horizontally sheared flow in the presence of rotation. Examination of enstrophy budgets in cases which are initially inertially unstable reveal the importance of baroclinic torque in maintaining lateral enstrophy fluctuations substantially beyond the time when the flow becomes inertially stable. The cyclonic stratified cases show weak nonlinearity in vortex dynamics. At high Reynolds number, despite the strong stratification, the flow exhibits three-dimensional, nonlinear dynamics and significant vertical mixing except for cases where the rotation is stabilizing.

JFM classification

Turbulent Flows: Rotating turbulence Turbulent Flows: Stratified turbulence Turbulent Flows: Turbulent Flows
Type
Papers
Information
Journal of Fluid Mechanics , Volume 732 , 10 October 2013 , pp. 373 - 400
Copyright
©2013 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Afanasyev, Y. D. & Peltier, W. R. 1998 The three-dimensionalization of stratified flow over two-dimensional topography. J. Atmos. Sci. 55, 19–39.Google Scholar
Arobone, E. & Sarkar, S. 2010 The statistical evolution of a stratified mixing layer with horizontal shear invoking feature extraction. Phys. Fluids 22, 115108.Google Scholar
Arobone, E. & Sarkar, S. 2012 Evolution of a stratified rotating shear layer with horizontal shear. Part I. Linear stability. J. Fluid Mech. 703, 29–48.Google Scholar
Bartello, P., Métais, O. & Lesieur, M. 1994 Coherent structures in rotating three-dimensional turbulence. J. Fluid Mech. 273, 1–29.Google Scholar
Basak, S. & Sarkar, S. 2006 Dynamics of a stratified shear layer with horizontal shear. J. Fluid Mech. 568, 19–54.Google Scholar
Billant, P. & Chomaz, J.-M. 2000 Experimental evidence for a new instability of a vertical columnar vortex pair in a strongly stratified fluid. J. Fluid Mech. 418, 167–188.Google Scholar
Carnevale, G. F., Kloosterziel, R. C., Orlandi, P. & van Sommeren, D. D. J. A. 2011 Predicting the aftermath of vortex breakup in rotating flow. J. Fluid Mech. 669, 90–119.Google Scholar
Flament, P., Lumpkin, R., Tournadre, J. & Armi, L. 2001 Vortex pairing in an unstable anticyclonic shear flow: discrete subharmonics of one pendulum day. J. Fluid Mech. 440, 401–409.Google Scholar
Jeong, J. & Hussain, F. 1995 On the identification of a vortex. J. Fluid Mech. 285, 69–94.Google Scholar
Kloosterziel, R. C., Carnevale, G. F. & Orlandi, P. 2007a Inertial instability in rotating and stratified fluids: barotropic vortices. J. Fluid Mech. 583, 379–412.CrossRefGoogle Scholar
Kloosterziel, R. C. & van Heijst, G. J. F. 1991 An experimental study of unstable barotropic vortices in a rotating fluid. J. Fluid Mech. 223, 1–24.Google Scholar
Kloosterziel, R. C., Orlandi, P. & Carnevale, G. F. 2007b Saturation of inertial instability in rotating planar shear flows. J. Fluid Mech. 583, 413–422.Google Scholar
Lesieur, M., Yanase, S. & Métais, O. 1991 Stabilizing and destabilizing effects of a solid-body rotation on quasi-two-dimensional shear layers. Phys. Fluids A 3 (3), 403–407.Google Scholar
Métais, O., Flores, C., Yanase, S., Riley, J. J. & Lesieur, M. 1995 Rotating free-shear flows. Part 2. Numerical simulations. J. Fluid Mech. 293, 47–80.Google Scholar
Otheguy, P., Billant, P. & Chomaz, J.-M. 2006a Elliptic and zigzag instabilities on co-rotating vertical vortices in a stratified fluid. J. Fluid Mech. 553, 253–272.Google Scholar
Otheguy, P., Billant, P. & Chomaz, J.-M. 2006b The effect of planetary rotation on the zigzag instability of co-rotating vortices in a stratified fluid. J. Fluid Mech. 553, 273–281.Google Scholar
Plougonven, R. & Zeitlin, V. 2009 Nonlinear development of inertial instability in a barotropic shear. Phys. Fluids 21, 106601.CrossRefGoogle Scholar
Potylitsin, P. G. & Peltier, W. R. 1998 Stratification effects on the stability of columnar vortices on the $f$ -plane. J. Fluid Mech. 355, 45–79.CrossRefGoogle Scholar
Potylitsin, P. G. & Peltier, W. R. 1999 Three-dimensional destabilization of stuart vortices. J. Fluid Mech. 387, 205–226.CrossRefGoogle Scholar
Potylitsin, P. G. & Peltier, W. R. 2003 On the nonlinear evolution of columnar vortices in a rotating environment. Geophys. Astrophys. Fluid Dyn. 97, 365–391.Google Scholar
Praud, O., Sommeria, J. & Fincham, A. M. 2006 Decaying grid turbulence in a rotating stratified tank. J. Fluid Mech. 547, 389–412.CrossRefGoogle Scholar
Riley, J. J. & de Bruyn Kops, S. M. 2003 Dynamics of turbulence strongly influenced by buoyancy. Phys. Fluids 15 (7), 2047–2059.Google Scholar
Smith, L. M. & Waleffe, F. 2002 Generation of slow large-scales in forced rotating stratified turbulence. J. Fluid Mech. 451, 145–168.Google Scholar
Yanase, S., Flores, C., Métais, O. & Riley, J. J. 1993 Rotating free-shear flows. I. Linear stability analysis. Phys. Fluids 5 (11), 2725–2737.Google Scholar