Hostname: page-component-586b7cd67f-rcrh6 Total loading time: 0 Render date: 2024-11-23T03:49:49.806Z Has data issue: false hasContentIssue false
  • English
  • Français

Evolution and stationarity of liquid toroidal drop in compressional Stokes flow

Published online by Cambridge University Press:  27 November 2017

B. K. Ee ,
O. M. Lavrenteva ,
I. Smagin  and
A. Nir Open the ORCID record for A. Nir [Opens in a new window]
B. K. Ee
Affiliation:
Department of Chemical Engineering, Technion-Israel Institute of Technology, Haifa 3200003, Israel
O. M. Lavrenteva
Affiliation:
Department of Chemical Engineering, Technion-Israel Institute of Technology, Haifa 3200003, Israel
I. Smagin
Affiliation:
Department of Chemical Engineering, Technion-Israel Institute of Technology, Haifa 3200003, Israel
A. Nir*
Affiliation:
Department of Chemical Engineering, Technion-Israel Institute of Technology, Haifa 3200003, Israel
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Dynamics of fluid tori in slow viscous flow is studied. Such tori are of interest as future carriers of biological and medicinal substances and are also viewed as potential building blocks towards more complex particles. In this study the immiscible ambient fluid is subject to a compressional flow (i.e., bi-extensional flow), and it comprises a generalization of our earlier report on the particular case with viscosity ratio 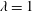$\unicode[STIX]{x1D706}=1$ (see Zabarankin et al., J. Fluid Mech., vol. 785, 2015, pp. 372–400), where 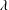$\unicode[STIX]{x1D706}$ is the ratio between the torus viscosity and that of the ambient fluid. It is found that, for all viscosity ratios, the torus either collapses towards the axis of symmetry or expands indefinitely, depending on the initial conditions and the capillary number, Ca. During these dynamic patterns the cross-sections exhibit various forms of deformation. The collapse and expansion dynamic modes are separated by a limited deformation into a deformed stationary state which appears to exist in a finite interval of the capillary number, 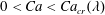$0<Ca<Ca_{cr}(\unicode[STIX]{x1D706})$, and is unstable to axisymmetric disturbances, which eventually cause the torus either to collapse or to expand indefinitely. The characteristic dimensions and shapes of these unstable stationary tori and their dependence on the physical parameters Ca and 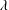$\unicode[STIX]{x1D706}$ are reported.

JFM classification

Low-Reynolds-number flows: Boundary integral methods Drops and Bubbles: Drops and Bubbles Low-Reynolds-number flows: Low-Reynolds-number flows
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 835 , 25 January 2018 , pp. 1 - 23
Check for updates
Copyright
© 2017 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Acrivos, A. & Lo, T. S. 1978 Deformation and breakup of a single slender drop in an extensional flow. J. Fluid. Mech. 86, 641–672.Google Scholar
An, D., Warning, A., Yancey, K. G., Chang, C. T., Kern, V. R., Datta, A. K., Steen, P. H., Luo, D. & Ma, M. 2016 Mass production of shaped particles through vortex ring freezing. Nat. Commun. 7, 12401.Google Scholar
Baumann, N., Josef, D. D., Mohr, P. & Renardy, Y. 1992 Vortex ring of one fluid in another in free fall. Phys. Fluids A 4, 567–580.Google Scholar
Bosse, T., Kleiser, L., Härtel, C. & Meiburg, E. 2005 Numerical simulation of finite Reynolds number suspension drops settling under gravity. Phys. Fluids 3, 037101.Google Scholar
Champion, J. A., Katare, Y. K. & Mitragotri, S. 2007 Particle shape: a new design parameter for micro-, and nanoscale drug delivery carriers. J. Control. Release 121 (1-2), 3–9.Google Scholar
Chang, Y. W., Fragkopoulos, A. A., Marquez, S. M., Kim, H. D., Angelini, T. E. & Fernandes-Nieves, A. 2015 Biofilm formation in geometries with different surface curvature and oxygen availability. New J. Phys. 17, 033017.Google Scholar
Chen, C. H., Shah, R. K., Abate, A. R. & Weitz, D. A. 2009 Janus particles templated from double emulsion droplets generated using microfluidics. Langmuir 25, 4320–4320.Google Scholar
Dean, D. M., Napolitano, A. P., Youssef, J. & Morgan, J. R. 2007 Rods, tori, and honeycombs: The directed self-assembly of microtissues with prescribed microscale geometries. FASEB J. 21 (14), 4005–4012.Google Scholar
Deshmukh, S. D. & Thaokar, R. M. 2013 Deformation and breakup of a leaky dielectric drop in a quadrupole electric field. J. Fluid Mech. 731 (4), 713–733.Google Scholar
Ghazian, O., Adamiak, K. & Castle, G. S. P. 2013 Numerical simulation of electrically deformed droplets less conductive than ambient fluid. Colloids Surf. A 43, 27–34.Google Scholar
Karyappa, R. B., Deshmukh, S. D. & Thaokar, R. M. 2014 Breakup of a conducting drop in a uniform electric field. J. Fluid Mech. 754, 550–589.Google Scholar
Kojima, M., Hinch, E. J. & Acrivos, A. 1984 The formation and expansion of a toroidal drop moving in a viscous fluid. Phys. Fluids 27 (1), 19–32.Google Scholar
Machu, G., Meile, W., Nitsche, L. C. & Schaflinger, U. 2001a Coalescence, torus formation and breakup of sedimenting drops: experiments and computer simulations. J. Fluid Mech. 447, 299–336.Google Scholar
Machu, G., Meile, W., Nitsche, L. C. & Schaflinger, U. 2001b The motion of a swarm of particles travelling through a quiescent, viscous fluid. Z. Angew. Math. Mech. 81 (s3), 547–548.CrossRefGoogle Scholar
Mehrabian, H. & Feng, J. J. 2013 Capillary breakup of a liquid torus. J. Fluid Mech. 717, 281–292.Google Scholar
Menchaca-Rocha, A., Borunda, M., Hidalgo, S. S., Huidobro, F., Michaelian, K. A., Pérez, A. & Rodríguez, V. 1996 Are the toroidal shapes of heavy-ion reactions seen in macroscopic drop collisions? Rev. Mex. Fiz. 42 (Suplemento), 198–202.Google Scholar
Nurse, A., Freund, L. B. & Youseff, J. 2012 A model of force generation in a three-dimensional toroidal cluster of cells. J. Appl. Mech. 79, 051013.Google Scholar
Pairam, E. & Fernández-Nieves, A. 2009 Generation and stability of toroidal droplets in a viscous liquid. Phys. Rev. Lett. 102, 234501.Google Scholar
Plateau, J. 1857 I. experimental and theoretical researches on the figures of equilibrium of a liquid mass withdrawn from the action of gravity. Third series. Phil. Mag. 14 (90), 1–22.CrossRefGoogle Scholar
Pozrikidis, C. 1992 Boundary Integral and Singularity Methods for Linearized Viscous Flow. Cambridge University Press.Google Scholar
Rallison, J. M. & Acrivos, A. 1978 A numerical study of the deformation and burst of a viscous drop in an extensional flow. J. Fluid Mech. 89, 191–200.Google Scholar
Renardy, Y., Popinet, S., Duchemin, L., Renardy, M., Zaleski, S., Josserand, C., Drumright-Clarke, D., Richard, M. A., Clanet, C. & Quéré, D. 2003 Pyramidal and toroidal water drops after impact on a solid surface. J. Fluid Mech. 484, 69–83.CrossRefGoogle Scholar
Sharma, V., Szymusiak, M., Shen, H., Nitsche, L. C. & Liu, Y. 2012 Formation of polymeric toroidal-spiral particles. Langmuir 28, 729–735.Google Scholar
Shum, H. C., Abate, A. R., Lee, D. A., Studart, R., Wang, B., Chen, C. H., Thiele, J., Shah, R. K., Krummel, A. & Weitz, D. A. 2010 Droplet microfluidics for fabrication of non-spherical particles. Macromol. Rapid Commun. 31, 108–118.Google Scholar
Sostarecz, M. C. & Belmonte, A. 2003 Motion and shape of viscoelastic drop falling through viscous fluid. J. Fluid Mech. 497, 235–252.Google Scholar
Stone, H. A. & Leal, L. G. 1989 A note concerning drop deformation and breakup in biaxial extensional flows at low Reynolds numbers. J. Colloid Interface Sci. 133, 340–347.CrossRefGoogle Scholar
Szymusiak, M., Sharma, V., Nitsche, L. C. & Liu, Y. 2012 Interaction of sedimenting drops in a miscible solution formation of heterogeneous toroidal-spiral particles. Soft Matt. 8, 7556–7559.Google Scholar
Texier, B. D., Piroird, K., Quere, D. & Clanet, C. 2013 Inertial collapse of liquid rings. J. Fluid Mech. 717, R3.CrossRefGoogle Scholar
Zabarankin, M. 2016 Liquid toroidal drop in compressional flow with arbitrary drop-to-ambient fluid viscosity ratio. Proc. R. Soc. Lond. A 472, 2187.Google Scholar
Zabarankin, M., Lavrenteva, O. M. & Nir, A. 2015 Liquid toroidal drop in compressional Stokes flow. J. Fluid Mech. 785, 372–400.Google Scholar
Zabarankin, M., Smagin, I., Lavrenteva, O. M. & Nir, A. 2013 Viscous drop in compressional Stokes flow. J. Fluid Mech. 720, 169–191.Google Scholar