Hostname: page-component-586b7cd67f-rcrh6 Total loading time: 0 Render date: 2024-11-22T19:15:59.008Z Has data issue: false hasContentIssue false
  • English
  • Français

Evidence that uniform momentum zones originate from roughness sublayer structure interactions in fully rough channel turbulence

Published online by Cambridge University Press:  30 June 2022

Y. Zheng  and
W. Anderson Open the ORCID record for W. Anderson [Opens in a new window]
Y. Zheng
Affiliation:
Department of Mechanical Engineering, University of Texas at Dallas, Richardson, TX 75080, USA
W. Anderson*
Affiliation:
Department of Mechanical Engineering, University of Texas at Dallas, Richardson, TX 75080, USA
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

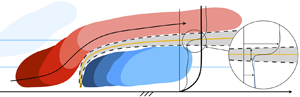
Fully rough wall-sheared turbulence is composed of an inner and outer layer, the former occupied by sinuous structures sustained by the well-known autonomous inner cycle, the latter occupied by inclined parcels of momentum deviations relative to the average. The outer-layer structures are also known as uniform momentum zones (UMZs), where the presence of successive UMZs manifests instantaneously with a distinct ‘staircase’ pattern in streamwise velocity. Direct numerical simulation (DNS) of fully rough channel turbulence was recently used to interpret UMZs as wakes originating from antecedent bluff-body-like interactions within the inner layer (Anderson & Salesky, J. Fluid Mech., vol. 906, 2020, A8). Wake-scaling arguments agreed precisely with instantaneous results from DNS. Foremost among these results was evidence that the instantaneous wall-normal gradient of streamwise velocity exhibited scaling of ${\sim }x_3^{-1/2}$, where $x_3$ is wall-normal location; this is in contrast to logarithmic scaling, which requires the wall-normal gradient of streamwise velocity to scale as ${\sim }x_3^{-1}$. Herein, wake-scaling arguments have been advanced and compared against results from wall-modelled large-eddy simulation (LES). New results from the ‘bottom up’ wake-scaling arguments agree with LES results, such that the shear associated with the instantaneous staircase-like streamwise velocity follows a clear trend. We have leveraged conditional sampling during LES – predicated upon instantaneous low-frequency, high-magnitude surface stress values known to correspond to large-scale inertial-layer coherence – to further assess the predictive value of the wake-scaling arguments. Model results compare favourably.

JFM classification

Turbulent Flows: Turbulence modelling Turbulent Flows: Turbulence theory Turbulent Flows: Turbulent boundary layers
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 944 , 10 August 2022 , A33
Check for updates
Copyright
© The Author(s), 2022. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

Adrian, R.J. 2007 Hairpin vortex organization in wall turbulence. Phys. Fluids 19, 041301.10.1063/1.2717527CrossRefGoogle Scholar
Adrian, R.J., Meinhart, C.D. & Tomkins, C.D. 2000 Vortex organization in the outer region of the turbulent boundary layer. J. Fluid Mech. 422, 1–54.10.1017/S0022112000001580CrossRefGoogle Scholar
Anderson, W. 2016 Amplitude modulation of streamwise velocity fluctuations in the roughness sublayer: evidence from large-eddy simulations. J. Fluid Mech. 789, 567–588.10.1017/jfm.2015.744CrossRefGoogle Scholar
Anderson, W., Barros, J.M., Christensen, K.T. & Awasthi, A. 2015 Numerical and experimental study of mechanisms responsible for turbulent secondary flows in boundary layer flows over spanwise heterogeneous roughness. J. Fluid Mech. 768, 316–347.10.1017/jfm.2015.91CrossRefGoogle Scholar
Anderson, W. & Meneveau, C. 2010 A large-eddy simulation model for boundary-layer flow over surfaces with horizontally resolved but vertically unresolved roughness elements. Boundary-Layer Meteorol. 137, 397–415.10.1007/s10546-010-9537-5CrossRefGoogle Scholar
Anderson, W. & Salesky, S.T. 2021 Uniform momentum zone scaling arguments from direct numerical simulation of inertia-dominated channel turbulence. J. Fluid Mech. 906, A8.10.1017/jfm.2020.800CrossRefGoogle Scholar
Antonia, R.A. 1981 Conditional sampling in turbulence measurement. Annu. Rev. Fluid Mech. 13, 131–156.10.1146/annurev.fl.13.010181.001023CrossRefGoogle Scholar
Balakumar, B.J. & Adrian, R.J. 2007 Large-and very-large-scale motions in channel and boundary-layer flows. Phil. Trans. R. Soc. A 365 (1852), 665–681.10.1098/rsta.2006.1940CrossRefGoogle ScholarPubMed
Bautista, J.C.C., Ebadi, A., White, C.M., Chini, G.P. & Klewicki, J.C. 2019 A uniform momentum zone–vortical fissure model of the turbulent boundary layer. J. Fluid Mech. 858, 609–633.10.1017/jfm.2018.769CrossRefGoogle Scholar
Bou-Zeid, E., Meneveau, C. & Parlange, M. 2005 A scale-dependent Lagrangian dynamic model for large eddy simulation of complex turbulent flows. Phys. Fluids 17 (2), 025105.10.1063/1.1839152CrossRefGoogle Scholar
Dong, S., Lozano-Duran, A., Sekimoto, A. & Jimenez, J. 2017 Coherent structures in statistically stationary homogeneous shear turbulence. J. Fluid Mech. 816, 167–208.10.1017/jfm.2017.78CrossRefGoogle Scholar
Fan, D., Xu, J., Yao, M.X. & Hickey, J.-P. 2019 On the detection of internal interfacial layers in turbulent flows. J. Fluid Mech. 872, 198–217.10.1017/jfm.2019.343CrossRefGoogle Scholar
Flack, K.A., Schultz, M.P. & Connelly, J.S. 2007 Examination of a critical roughness height for outer layer similarity. Phys. Fluids 19 (9), 095104.10.1063/1.2757708CrossRefGoogle Scholar
Ganapathisubramani, B., Longmire, E.K. & Marusic, I. 2003 Characteristics of vortex packets in turbulent boundary layers. J. Fluid Mech. 478, 35–46.10.1017/S0022112002003270CrossRefGoogle Scholar
Garratt, J.R. 1994 The Atmospheric Boundary Layer. Cambridge University Press.Google Scholar
Graham, J. & Meneveau, C. 2012 Modeling turbulent flow over fractal trees using renormalized numerical simulation: alternate formulations and numerical experiments. Phys. Fluids 24, 125105.10.1063/1.4772074CrossRefGoogle Scholar
Guala, M., Hommema, S.E. & Adrian, R.J. 2006 Large-scale and very-large-scale motions in turbulent pipe flow. J. Fluid Mech. 554, 521–542.10.1017/S0022112006008871CrossRefGoogle Scholar
Harmon, I. & Finnigan, J.J. 2007 A simple unified theory for flow in the canopy and roughness sublayer. Boundary-Layer Meteorol. 123, 339–364.10.1007/s10546-006-9145-6CrossRefGoogle Scholar
Heisel, M., de Silva, C.M., Hutchins, N., Marusic, I. & Guala, M. 2020 On the mixing length eddies and logarithmic mean velocity profile in wall turbulence. J. Fluid Mech. 887, R1.10.1017/jfm.2020.23CrossRefGoogle Scholar
Heisel, M., de Silva, C.M., Hutchins, N., Marusic, I. & Guala, M. 2021 Prograde vortices, internal shear layers and the Taylor microscale in high-Reynolds-number turbulent boundary layers. J. Fluid Mech. 920, A52.10.1017/jfm.2021.478CrossRefGoogle Scholar
Hutchins, N. & Marusic, I. 2007 Evidence of very long meandering features in the logarithmic region of turbulent boundary layers. J. Fluid Mech. 579, 1–28.10.1017/S0022112006003946CrossRefGoogle Scholar
Hutchins, N., Monty, J.P., Ganapathisubramani, B., Ng, H.C.H. & Marusic, I. 2011 Three-dimensional conditional structure of a high-Reynolds-number turbulent boundary layer. J. Fluid Mech. 673, 255–285.10.1017/S0022112010006245CrossRefGoogle Scholar
Hwang, Y. & Cossu, C. 2010 Self-sustained process at large scales in turbulent channel flow. Phys. Rev. Lett. 105, 044505–044505.10.1103/PhysRevLett.105.044505CrossRefGoogle ScholarPubMed
Jacob, C. & Anderson, W. 2017 Conditionally averaged large-scale motions in the neutral atmospheric boundary layer: insights for aeolian processes. Boundary-Layer. Meteorol. 162, 21–41.10.1007/s10546-016-0183-4CrossRefGoogle Scholar
Jimenez, J. 2004 Turbulent flow over rough wall. Annu. Rev. Fluid Mech. 36, 173–196.10.1146/annurev.fluid.36.050802.122103CrossRefGoogle Scholar
Jimenez, J. & Pinelli, A. 1999 The autonomous cycle of near-wall turbulence. J. Fluid Mech. 389, 335–359.10.1017/S0022112099005066CrossRefGoogle Scholar
Kim, K.C. & Adrian, R.J. 1999 Very large-scale motion in the outer layer. Phys. Fluids 11 (2), 417–422.10.1063/1.869889CrossRefGoogle Scholar
Klewicki, J.C. 2013 a A description of turbulent wall-flow vorticity consistent with mean dynamics. J. Fluid Mech. 737, 176–204.10.1017/jfm.2013.565CrossRefGoogle Scholar
Klewicki, J.C. 2013 b On the singular nature of turbulent boundary layers. Proc. IUTAM 9, 69–78.10.1016/j.piutam.2013.09.007CrossRefGoogle Scholar
Klewicki, J.C. 2013 c Self-similar mean dynamics in turbulent wall flows. J. Fluid Mech. 718, 596–621.10.1017/jfm.2012.626CrossRefGoogle Scholar
Kline, S.J., Reynolds, W.C., Schraub, F.A. & Rundstadler, P.W. 1967 The structure of turbulent boundary layers. J. Fluid Mech. 30, 741–773.10.1017/S0022112067001740CrossRefGoogle Scholar
Laskari, A., de Kat, R., Hearst, R.J. & Ganapathisubramani, B. 2018 Time evolution of uniform momentum zones in a turbulent boundary layer. J. Fluid Mech. 842, 554–590.10.1017/jfm.2018.126CrossRefGoogle Scholar
Lee, M. & Moser, R.D. 2015 Direct numerical simulation of turbulent channel flow up to $Re_\tau = 5200$. J. Fluid Mech. 774, 395–415.10.1017/jfm.2015.268CrossRefGoogle Scholar
Lee, M. & Moser, R.D. 2019 Spectral analysis of the budget equation in turbulent channel flows at high Reynolds number. J. Fluid Mech. 860, 886–938.10.1017/jfm.2018.903CrossRefGoogle Scholar
Marusic, I. & Heuer, W. 2007 Reynolds number invariance of the structure inclination angle in wall turbulence. Phys. Rev. Lett. 99 (11), 114504.10.1103/PhysRevLett.99.114504CrossRefGoogle ScholarPubMed
Marusic, I. & Hutchins, N. 2008 Study of the log-layer structure in wall turbulence over a very large range of Reynolds number. Flow Turbul. Combust. 81 (1–2), 115–130.10.1007/s10494-007-9116-0CrossRefGoogle Scholar
Marusic, I., Mathis, R. & Hutchins, N. 2010 Predictive model for wall-bounded turbulent flow. Science 329, 193–196.10.1126/science.1188765CrossRefGoogle ScholarPubMed
Mathis, R., Hutchins, N. & Marusic, I. 2009 Large-scale amplitude modulation of the small-scale structures in turbulent boundary layers. J. Fluid Mech. 628, 311–337.10.1017/S0022112009006946CrossRefGoogle Scholar
Mathis, R., Marusic, I., Chernyshenko, S.I. & Hutchins, N. 2013 Estimating wall-shear-stress fluctuations given an outer region input. J. Fluid Mech. 715, 163–180.10.1017/jfm.2012.508CrossRefGoogle Scholar
Meinhart, C.D. & Adrian, R.J. 1995 On the existence of uniform momentum zones in a turbulent boundary layer. Phys. Fluids 7, 694–696.10.1063/1.868594CrossRefGoogle Scholar
Montemuro, B., White, C.M., Klewicki, J.C. & Chini, G.P. 2020 A self-sustaining process theory for uniform momentum zones and internal shear layers in high Reynolds number shear flows. J. Fluid Mech. 901, A28–A28.10.1017/jfm.2020.517CrossRefGoogle Scholar
Morishita, K., Ishihara, T. & Kaneda, Y. 2019 Length scales in turbulent channel flow. J. Phys. Soc. Japan 88, 064401.10.7566/JPSJ.88.064401CrossRefGoogle Scholar
Pope, S.B. 2000 Turbulent Flows. Cambridge University Press.10.1017/CBO9780511840531CrossRefGoogle Scholar
Priyadarshana, P.J.A., Klewicki, J.C., Treat, S. & Foss, J.F. 2007 Statistical structure of turbulent boundary-layer velocity–vorticity products at high and low Reynolds numbers. J. Fluid Mech. 570, 307–346.10.1017/S0022112006002771CrossRefGoogle Scholar
Raupach, M.R., Antonia, R.A. & Rajagopalan, S. 1991 Rough-wall turbulent boundary layers. Appl. Mech. Rev. 44, 1–25.10.1115/1.3119492CrossRefGoogle Scholar
Schoppa, W. & Hussain, F. 2002 Coherent structure generation in near-wall turbulence. J. Fluid Mech. 453, 57–108.10.1017/S002211200100667XCrossRefGoogle Scholar
Sheng, J., Malkiel, E. & Katz, J. 2009 Buffer layer structures associated with extreme wall stress events in a smooth wall turbulent boundary layer. J. Fluid Mech. 633, 17–60.10.1017/S0022112009006934CrossRefGoogle Scholar
de Silva, C.M., Philip, J., Hutchins, N. & Marusic, I. 2017 Interfaces of uniform momentum zones in turbulent boundary layers. J. Fluid Mech. 820, 451–478.10.1017/jfm.2017.197CrossRefGoogle Scholar
Tennekes, H. & Lumley, J.L. 1972 A First Course in Turbulence. MIT Press.10.7551/mitpress/3014.001.0001CrossRefGoogle Scholar
Townsend, A.A. 1951 The structure of the turbulent boundary layer. Math. Proc. Camb. Phil. Soc. 47, 375–395.10.1017/S0305004100026724CrossRefGoogle Scholar
Volino, R.J., Schultz, M.P. & Flack, K.A. 2007 Turbulence structure in rough- and smooth-wall boundary layers. J. Fluid Mech. 592, 263–293.10.1017/S0022112007008518CrossRefGoogle Scholar
Wallace, J.M. 2016 Quadrant analysis in turbulence research: history and evolution. Annu. Rev. Fluid Mech. 3648, 131–158.10.1146/annurev-fluid-122414-034550CrossRefGoogle Scholar
Wu, Y. & Christensen, K.T. 2007 Outer-layer similarity in the presence of a practical rough-wall topology. Phys. Fluids 19, 085108.10.1063/1.2741256CrossRefGoogle Scholar
Wu, Y. & Christensen, K.T. 2010 Spatial structure of a turbulent boundary layer with irregular surface roughness. J. Fluid Mech. 655, 380–418.10.1017/S0022112010000960CrossRefGoogle Scholar
Zhu, X., Iungo, G.V., Leonardi, S. & Anderson, W. 2017 Parametric study of urban-like topographic statistical moments relevant to a priori modelling of bulk aerodynamic parameters. Boundary-Layer Meteorol. 162, 231–253.10.1007/s10546-016-0198-xCrossRefGoogle Scholar