Hostname: page-component-78c5997874-dh8gc Total loading time: 0 Render date: 2024-11-05T11:37:43.223Z Has data issue: false hasContentIssue false
  • English
  • Français

Evaluation of turbulent mixing transition in a shock-driven variable-density flow

Published online by Cambridge University Press:  20 October 2017

Mohammad Mohaghar ,
John Carter ,
Benjamin Musci ,
David Reilly ,
Jacob McFarland  and
Devesh Ranjan Open the ORCID record for Devesh Ranjan [Opens in a new window]
Mohammad Mohaghar
Affiliation:
George W. Woodruff School of Mechanical Engineering, Georgia Institute of Technology, USA
John Carter
Affiliation:
George W. Woodruff School of Mechanical Engineering, Georgia Institute of Technology, USA
Benjamin Musci
Affiliation:
George W. Woodruff School of Mechanical Engineering, Georgia Institute of Technology, USA
David Reilly
Affiliation:
George W. Woodruff School of Mechanical Engineering, Georgia Institute of Technology, USA
Jacob McFarland
Affiliation:
Department of Mechanical and Aerospace Engineering, University of Missouri, USA
Devesh Ranjan*
Affiliation:
George W. Woodruff School of Mechanical Engineering, Georgia Institute of Technology, USA
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

The effect of initial conditions on transition to turbulence is studied in a variable-density shock-driven flow. Richtmyer–Meshkov instability (RMI) evolution of fluid interfaces with two different imposed initial perturbations is observed before and after interaction with a second shock reflected from the end wall of a shock tube (reshock). The first perturbation is a predominantly single-mode long-wavelength interface which is formed by inclining the entire tube to 80$^{\circ }$ relative to the horizontal, yielding an amplitude-to-wavelength ratio, 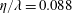$\unicode[STIX]{x1D702}/\unicode[STIX]{x1D706}=0.088$, and thus can be considered as half the wavelength of a triangular wave. The second interface is multi-mode, and contains additional shorter-wavelength perturbations due to the imposition of shear and buoyancy on the inclined perturbation of the first case. In both cases, the interface consists of a nitrogen-acetone mixture as the light gas over carbon dioxide as the heavy gas (Atwood number, 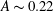$A\sim 0.22$) and the shock Mach number is 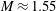$M\approx 1.55$. The initial condition was characterized through Proper Orthogonal Decomposition and density energy spectra from a large set of initial condition images. The evolving density and velocity fields are measured simultaneously using planar laser-induced fluorescence (PLIF) and particle image velocimetry (PIV) techniques. Density, velocity, and density–velocity cross-statistics are calculated using ensemble averaging to investigate the effects of additional modes on the mixing and turbulence quantities. The density and velocity data show that a distinct memory of the initial conditions is maintained in the flow before interaction with reshock. After reshock, the influence of the long-wavelength inclined perturbation present in both initial conditions is still apparent, but the distinction between the two cases becomes less evident as smaller scales are present even in the single-mode case. Several methods are used to calculate the Reynolds number and turbulence length scales, which indicate a transition to a more turbulent state after reshock. Further evidence of transition to turbulence after reshock is observed in the velocity and density fluctuation spectra, where a scaling close to 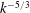$k^{-5/3}$ is observed for almost one decade, and in the enstrophy fluctuation spectra, where a scaling close to 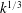$k^{1/3}$ is observed for a similar range. Also, based on normalized cross correlation spectra, local isotropy is reached at lower wave numbers in the multi-mode case compared with the single-mode case before reshock. By breakdown of large scales to small scales after reshock, rapid decay can be observed in cross-correlation spectra in both cases.

JFM classification

Compressible Flows: Shock waves Instability: Transition to turbulence Mixing: Turbulent mixing
Type
Papers
Information
Journal of Fluid Mechanics , Volume 831 , 25 November 2017 , pp. 779 - 825
Check for updates
Copyright
© 2017 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

‡

These two authors contributed equally.

References

Balakumar, B. J., Orlicz, G. C., Ristorcelli, J. R., Balasubramanian, S., Prestridge, K. P. & Tomkins, C. D. 2012 Turbulent mixing in a Richtmyer–Meshkov fluid layer after reshock: velocity and density statistics. J. Fluid Mech. 696, 67–93.CrossRefGoogle Scholar
Balakumar, B. J., Orlicz, G. C., Tomkins, C. D. & Prestridge, K. P. 2008 Simultaneous particle-image velocimetry–planar laser-induced fluorescence measurements of Richtmyer–Meshkov instability growth in a gas curtain with and without reshock. Phys. Fluids 20 (12), 124103.Google Scholar
Banerjee, A. & Andrews, M. J. 2009 3d simulations to investigate initial condition effects on the growth of Rayleigh–Taylor mixing. Intl J. Heat Mass Transfer 52 (17), 3906–3917.CrossRefGoogle Scholar
Batchelor, G. K. 1969 Computation of the energy spectrum in homogeneous two-dimensional turbulence. Phys. Fluids 12 (12), II–233.Google Scholar
Bendat, J. S. & Piersol, A. G. 2011 Random Data: Analysis and Measurement Procedures. Wiley.Google Scholar
Benedict, L. H. & Gould, R. D. 1996 Towards better uncertainty estimates for turbulence statistics. Exp. Fluids 22 (2), 129–136.Google Scholar
Berkooz, G., Holmes, P. & Lumley, J. L. 1993 The proper orthogonal decomposition in the analysis of turbulent flows. Annu. Rev. Fluid Mech. 25 (1), 539–575.CrossRefGoogle Scholar
Besnard, D., Harlow, F. H., Rauenzahn, R. M. & Zemach, C.1992 Turbulence transport equations for variable-density turbulence and their relationship to two-field models. Tech. Rep. lA-12303-MS. Los Alamos National Laboratory.CrossRefGoogle Scholar
Brouillette, M. & Sturtevant, B. 1994 Experiments on the Richtmyer–Meshkov instability: single-scale perturbations on a continuous interface. J. Fluid Mech. 263, 271–292.CrossRefGoogle Scholar
Charonko, J. J. & Vlachos, P. P. 2013 Estimation of uncertainty bounds for individual particle image velocimetry measurements from cross-correlation peak ratio. Meas. Sci. Technol. 24 (6), 065301.CrossRefGoogle Scholar
Collins, B. D. & Jacobs, J. W. 2002 PLIF flow visualization and measurements of the Richtmyer–Meshkov instability of an air/SF6 interface. J. Fluid Mech. 464, 113–136.CrossRefGoogle Scholar
Cook, A. W. 2007 Artificial fluid properties for large-eddy simulation of compressible turbulent mixing. Phys. Fluids 19 (5), 055103.Google Scholar
Cook, A. W. & Cabot, W. H. 2005 Hyperviscosity for shock-turbulence interactions. J. Comput. Phys. 203 (2), 379–385.Google Scholar
Dimotakis, P. E. 2000 The mixing transition in turbulent flows. J. Fluid Mech. 409, 69–98.Google Scholar
Dimotakis, P. E. 2005 Turbulent mixing. Annu. Rev. Fluid Mech. 37, 329–356.Google Scholar
George, W. K. 2008 Is there an asymptotic effect of initial and upstream conditions on turbulence? In ASME 2008 Fluids Engineering Division Summer Meeting collocated with the Heat Transfer, Energy Sustainability, and 3rd Energy Nanotechnology Conferences, pp. 647–672. American Society of Mechanical Engineers.Google Scholar
George, W. K. & Davidson, L. 2004 Role of initial conditions in establishing asymptotic flow behavior. AIAA J. 42 (3), 438–446.Google Scholar
Houas, L. & Chemouni, I. 1996 Experimental investigation of Richtmyer–Meshkov instability in shock tube. Phys. Fluids 8 (2), 614–627.Google Scholar
Jacobs, J. W., Krivets, V. V., Tsiklashvili, V. & Likhachev, O. A. 2013 Experiments on the Richtmyer–Meshkov instability with an imposed, random initial perturbation. Shock Waves 23 (4), 407–413.Google Scholar
Jacobs, J. W. & Sheeley, J. M. 1996 Experimental study of incompressible Richtmyer–Meshkov instability. Phys. Fluids 8 (2), 405–415.Google Scholar
Kane, J., Drake, R. P. & Remington, B. A. 1999 An evaluation of the Richtmyer–Meshkov instability in supernova remnant formation. Astrophys. J. 511 (1), 335–340.Google Scholar
Kifonidis, K., Plewa, T., Scheck, L., Janka, H. & Müller, E. 2006 Non-spherical core collapse supernovae-II. The late-time evolution of globally anisotropic neutrino-driven explosions and their implications for SN 1987 A. Astron. Astrophys. 453 (2), 661–678.Google Scholar
Kraichnan, R. H. 1967 Inertial ranges in two-dimensional turbulence. Phys. Fluids 10 (7), 1417–1423.Google Scholar
Kuchibhatla, S. & Ranjan, D. 2013 Effect of initial conditions on Rayleigh–Taylor mixing: modal interaction. Phys. Scr. 2013 (T155), 014057.Google Scholar
Latini, M., Schilling, O. & Don, W. 2007 Effects of WENO flux reconstruction order and spatial resolution on reshocked two-dimensional Richtmyer–Meshkov instability. J. Comput. Phys. 221 (2), 805–836.Google Scholar
Lavoie, P., Avallone, G., De Gregorio, F., Romano, G. & Antonia, R. 2007 Spatial resolution of PIV for the measurement of turbulence. Exp. Fluids 43 (1), 39–51.Google Scholar
Lindl, J., Landen, O., Edwards, J., Moses, E. D.& NIC Team 2014 Review of the National Ignition Campaign 2009–2012. Phys. Plasmas 21 (2), 020501.Google Scholar
Livescu, D. & Ristorcelli, J. R. 2008 Variable-density mixing in buoyancy-driven turbulence. J. Fluid Mech. 605, 145–180.Google Scholar
Lombardini, M., Pullin, D. I. & Meiron, D. I. 2012 Transition to turbulence in shock-driven mixing: a Mach number study. J. Fluid Mech. 690, 203–226.Google Scholar
McFarland, J., Greenough, J. & Ranjan, D. 2014a Simulations and analysis of the reshocked inclined interface Richtmyer–Meshkov instability for linear and nonlinear interface perturbations. Trans. ASME: J. Fluids Engng 136 (7), 071203.Google Scholar
McFarland, J., Reilly, D., Creel, S., McDonald, C., Finn, T. & Ranjan, D. 2014b Experimental investigation of the inclined interface Richtmyer–Meshkov instability before and after reshock. Exp. Fluids 55 (1), 1–14.CrossRefGoogle Scholar
McFarland, J. A., Greenough, J. A. & Ranjan, D. 2011 Computational parametric study of a Richtmyer–Meshkov instability for an inclined interface. Phys. Rev. E 84 (2), 026303.Google Scholar
Mcfarland, J. A., Reilly, D., Black, W., Greenough, J. A. & Ranjan, D. 2015 Modal interactions between a large-wavelength inclined interface and small-wavelength multimode perturbations in a Richtmyer–Meshkov instability. Phys. Rev. E 92 (1), 013023.Google Scholar
Meshkov, E. E. 1969 Instability of the interface of two gases accelerated by a shock wave. Fluid Dyn. 4 (5), 101–104.Google Scholar
Mikaelian, K. O. 2016 Oscillations of a standing shock wave generated by the Richtmyer–Meshkov instability. Phys. Rev. Fluids 1 (3), 033601.Google Scholar
Morgan, R. V., Aure, R., Stockero, J. D., Greenough, J. A., Cabot, W., Likhachev, O. A. & Jacobs, J. W. 2012 On the late-time growth of the two-dimensional Richtmyer–Meshkov instability in shock tube experiments. J. Fluid Mech. 712, 354–383.Google Scholar
Orlicz, G. C., Balasubramanian, S., Vorobieff, P. & Prestridge, K. P. 2015 Mixing transition in a shocked variable-density flow. Phys. Fluids 27 (11), 114102.Google Scholar
Pope, S. B. 2000 Turbulent Flows. Cambridge University Press.CrossRefGoogle Scholar
Quirk, J. J. & Karni, S. 1996 On the dynamics of a shock–bubble interaction. J. Fluid Mech. 318, 129–163.Google Scholar
Ramaprabhu, P. & Andrews, M. J. 2004 Experimental investigation of Rayleigh–Taylor mixing at small Atwood numbers. J. Fluid Mech. 502, 233–271.Google Scholar
Ranjan, D., Oakley, J. & Bonazza, R. 2011 Shock-bubble interactions. Annu. Rev. Fluid Mech. 43, 117–140.Google Scholar
Reilly, D.2015 Experimental study of shock-driven, variable-density turbulence using a complex interface. Master’s thesis, Georgia Institute of Technology.Google Scholar
Reilly, D., McFarland, J., Mohaghar, M. & Ranjan, D. 2015 The effects of initial conditions and circulation deposition on the inclined-interface reshocked Richtmyer–Meshkov instability. Exp. Fluids 56 (8), 1–16.Google Scholar
Richtmyer, R. D. 1960 Taylor instability in shock acceleration of compressible fluids. Commun. Pure Appl. Maths 13 (2), 297–319.Google Scholar
Robey, H. F., Zhou, Y. e., Buckingham, A. C., Keiter, P., Remington, B. A. & Drake, R. P. 2003 The time scale for the transition to turbulence in a high Reynolds number, accelerated flow. Phys. Plasmas 10 (3), 614–622.Google Scholar
Schilling, O., Latini, M. & Don, W. S. 2007 Physics of reshock and mixing in single-mode Richtmyer–Meshkov instability. Phys. Rev. E 76 (2), 026319.Google Scholar
Schwarzkopf, J. D., Livescu, D., Baltzer, J. R., Gore, R. A. & Ristorcelli, J. R. 2016 A two-length scale turbulence model for single-phase multi-fluid mixing. Flow Turbul. Combust. 96 (1), 1–43.Google Scholar
Shankar, S. K. & Lele, S. K. 2014 Numerical investigation of turbulence in reshocked Richtmyer–Meshkov unstable curtain of dense gas. Shock Waves 24 (1), 79–95.CrossRefGoogle Scholar
Shen, X. & Warhaft, Z. 2000 The anisotropy of the small scale structure in high Reynolds number (r𝜆 1000) turbulent shear flow. Phys. Fluids 12 (11), 2976–2989.Google Scholar
Soloff, S. M., Adrian, R. J. & Liu, Z. 1997 Distortion compensation for generalized stereoscopic particle image velocimetry. Meas. Sci. Technol. 8 (12), 1441.CrossRefGoogle Scholar
Stanislas, M. & Monnier, J. 1997 Practical aspects of image recording in particle image velocimetry. Meas. Sci. Technol. 8 (12), 1417.Google Scholar
Strutt, J. W. 1900 Investigation of the character of the equilibrium of an incompressible heavy fluid of variable density. In Scientific Papers, vol. 2, pp. 200–207.Google Scholar
Tavoularis, S. & Corrsin, S. 1981a Experiments in nearly homogeneous turbulent shear flow with a uniform mean temperature gradient. Part 2. The fine structure. J. Fluid Mech. 104, 349–367.Google Scholar
Tavoularis, S. & Corrsin, S. 1981b Experiments in nearly homogenous turbulent shear flow with a uniform mean temperature gradient. Part 1. J. Fluid Mech. 104, 311–347.Google Scholar
Taylor, G. 1950 The instability of liquid surfaces when accelerated in a direction perpendicular to their planes. Proc. R. Soc. I 201 (1065), 192–196.Google Scholar
Thornber, B., Drikakis, D., Youngs, D. L. & Williams, R. J. R. 2011 Growth of a Richtmyer–Meshkov turbulent layer after reshock. Phys. Fluids 23 (9), 095107.Google Scholar
Thornber, B., Drikakis, D., Youngs, D. L. & Williams, R. J. R. 2012 Physics of the single-shocked and reshocked Richtmyer–Meshkov instability. J. Turbul. 13 (1), N10.Google Scholar
Tomkins, C. D., Balakumar, B. J., Orlicz, G., Prestridge, K. P. & Ristorcelli, J. R. 2013 Evolution of the density self-correlation in developing Richtmyer–Meshkov turbulence. J. Fluid Mech. 735, 288–306.Google Scholar
Tritschler, V. K., Olson, B. J., Lele, S. K., Hickel, S., Hu, X. Y. & Adams, N. A. 2014 On the Richtmyer–Meshkov instability evolving from a deterministic multimode planar interface. J. Fluid Mech. 755, 429–462.Google Scholar
Vetter, M. & Sturtevant, B. 1995 Experiments on the Richtmyer–Meshkov instability of an air/SF6 interface. Shock Waves 4 (5), 247–252.Google Scholar
Vorobieff, P., Rightley, P. M. & Benjamin, R. F. 1998 Power-law spectra of incipient gas-curtain turbulence. Phys. Rev. Lett. 81 (11), 2240.Google Scholar
Waitz, I. A., Marble, F. E. & Zukoski, E. E. 1993 Investigation of a contoured wall injector for hypervelocity mixing augmentation. AIAA J. 31 (6), 1014–1021.Google Scholar
Weber, C., Cook, A. & Bonazza, R. 2013 Growth rate of a shocked mixing layer with known initial perturbations. J. Fluid Mech. 725, 372–401.Google Scholar
Weber, C. R., Haehn, N., Oakley, J., Rothamer, D. & Bonazza, R. 2012 Turbulent mixing measurements in the Richtmyer–Meshkov instability. Phys. Fluids 24 (7), 074105.Google Scholar
Weber, C. R., Haehn, N. S., Oakley, J. G., Rothamer, D. A. & Bonazza, R. 2014 An experimental investigation of the turbulent mixing transition in the Richtmyer–Meshkov instability. J. Fluid Mech. 748, 457–487.Google Scholar
Xue, Z., Charonko, J. J. & Vlachos, P. P. 2014 Particle image velocimetry correlation signal-to-noise ratio metrics and measurement uncertainty quantification. Meas. Sci. Technol. 25 (11), 115301.Google Scholar
Yang, Q., Chang, J. & Bao, W. 2014 Richtmyer–Meshkov instability induced mixing enhancement in the scramjet combustor with a central strut. Adv. Mech. Engng 6, 614189.Google Scholar
Zhou, Y. 2017 Rayleigh–Taylor and Richtmyer–Meshkov instability induced flow, turbulence, and mixing. Phys. Rep. I.Google Scholar