Hostname: page-component-745bb68f8f-5r2nc Total loading time: 0 Render date: 2025-01-09T19:12:58.511Z Has data issue: false hasContentIssue false
  • English
  • Français

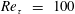Estimation of turbulent channel flow at $Re_{\unicode[STIX]{x1D70F}}~=~100$ based on the wall measurement using a simple sequential approach

Published online by Cambridge University Press:  05 October 2017

Takao Suzuki Open the ORCID record for Takao Suzuki [Opens in a new window]  and
Yosuke Hasegawa
Takao Suzuki*
Affiliation:
Graduate School of Engineering, University of Fukui, 3-9-1 Bunkyo, Fukui, 910-8507, Japan
Yosuke Hasegawa
Affiliation:
Institute of Industrial Science, The University of Tokyo, 4-6-1 Komaba, Meguro-ku, Tokyo, 153-8505, Japan
*
†Present address: Acoustics & Fluid Mechanics, The Boeing Company, Seattle, WA 98124-2207, USA. Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

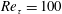The unsteady flow estimation problem of wall-bounded turbulence, numerically benchmarked by Chevalier et al. (J. Fluid Mech., vol. 552, 2006, pp. 167–187), is re-tackled with simple approaches. A turbulent channel flow at $Re_{\unicode[STIX]{x1D70F}}=100$ with periodic boundary conditions is reconstructed with linear stochastic estimation only based on the wall measurement, i.e. the wall shear stress in the streamwise and spanwise directions as well as the wall pressure over the entire wavenumber space. The results reveal that instantaneous information on the wall governs the success of the estimation in the vicinity of the wall (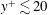$y^{+}\lesssim 20$). The degrees of agreement are equivalent to those reported by Chevalier et al. using the extended Kalman filter as well as the ensemble Kalman filter performed in this study. This suggests that the instantaneous information on the wall dictates the reconstruction rather than the prediction step in these state observers solving the dynamical system. Subsequently, we feed the velocity components given by the linear stochastic estimation via the body-force term into the Navier–Stokes system: such an observer slightly improves the estimation in the log layer, indicating a small benefit of involving a dynamical system but over-suppression of turbulent motions beyond the viscous sublayer due to their low correlation with the wall measurement. Errors in the estimation grow in the buffer layer and prevent further reconstruction toward the centreline even if we relax the feedback forcing and let the flow evolve nonlinearly through the observer. We also discuss the flow components truly reconstructible from the wall measurement, which has limited degrees of freedom and poor correlation across wavenumbers.

JFM classification

Turbulent Flows: Turbulence control Turbulent Flows: Turbulent Flows
Type
Papers
Information
Journal of Fluid Mechanics , Volume 830 , 10 November 2017 , pp. 760 - 796
Check for updates
Copyright
© 2017 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Adrian, R. J. & Moin, P. 1988 Stochastic estimation of organized turbulent structure: homogeneous shear flow. J. Fluid Mech. 190, 531–559.Google Scholar
Baars, W. J., Hutchins, N. & Marusic, I. 2016 Spectral stochastic estimation of high-Reynolds-number wall-bounded turbulence for a refined inner-outer interaction model. Phys. Rev. Fluids 1, 054406.Google Scholar
Bewley, T. R. 2001 Flow control: new challenges for a new Renaissance. Prog. Aerosp. Sci. 37 (1), 21–58.Google Scholar
Bewley, T. R., Moin, P. & Temam, R. 2001 DNS-based predictive control of turbulence: an optimal benchmark for feedback algorithm. J. Fluid Mech. 447, 179–225.Google Scholar
Bewley, T. R. & Protas, B. 2004 Skin friction and pressure: the ‘footprints’ of turbulence. Physica D 196, 28–44.Google Scholar
Brunton, S. L. & Noack, B. R. 2015 Closed-loop turbulence control: progress and challenges. Trans. ASME: Appl. Mech. Rev. 67 (5), 050801.Google Scholar
Bucy, R. S. & Joseph, P. D. 1968 Filtering for Stochastic Processes with Applications to Guidance. Wiley.Google Scholar
Chevalier, M., Hœpffner, J., Bewley, T. R. & Henningson, D. S. 2006 State estimation in wall-bounded flow systems. Part 2. Turbulent flows. J. Fluid Mech. 552, 167–187.CrossRefGoogle Scholar
Chevalier, M., Hœpffner, J. & Henningson, D. S. 2007 Linear feedback control and estimation applied to instabilities in spatially developing boundary layers. J. Fluid Mech. 588, 163–187.CrossRefGoogle Scholar
Colburn, C. H., Cessna, J. B. & Bewley, T. R. 2011 State estimation in wall-bounded flow systems. Part 3. The ensemble Kalman filter. J. Fluid Mech. 682, 289–303.CrossRefGoogle Scholar
Evensen, G. 1994 Sequential data assimilation with a non-linear quasi-geostrophic model using Monte Carlo methods to forecast error statistics. J. Geophys. Res. 99 (C5), 10143–10162.Google Scholar
Fulgosi, M., Lakehal, D., Banerjee, S. & Angelis, V. D. 2003 Direct numerical simulation of turbulence in a sheared air-water flow with a deformable interface. J. Fluid Mech. 482, 319–345.CrossRefGoogle Scholar
Hasegawa, Y. & Kasagi, N. 2011 Dissimilar control of momentum and heat transfer in a fully developed channel flow. J. Fluid Mech. 683, 57–93.CrossRefGoogle Scholar
Hœpffner, J., Chevalier, M., Bewley, T. R. & Henningson, D. S. 2005 State estimation in wall-bounded flow systems. Part 1. Perturbed laminar flows. J. Fluid Mech. 534, 263–294.Google Scholar
Högberg, M., Bewley, T. R. & Henningson, D. S. 2003 Linear feedback control and estimation of transition in plane channel flow. J. Fluid Mech. 481, 149–175.CrossRefGoogle Scholar
Iwamoto, K., Suzuki, Y. & Kasagi, N.2002 Database of fully developed channel flow. THTLAB Internal Report ILR0201, http://thtlab.jp/index-orig.html.Google Scholar
Jones, B. L., Kerrigan, E. C., Morrison, J. F. & Zaki, T. A. 2011 Flow estimation of boundary layers using DNS based wall shear information. Intl J. Control 84 (8), 1310–1325.CrossRefGoogle Scholar
Kalman, R. E. 1960 A new approach to linear filtering and prediction problems. Trans. ASME: J. Basic Engng 82 (D), 35–45.Google Scholar
Kim, J. & Bewley, T. R. 2007 Linear systems approach to flow control. Annu. Rev. Fluid Mech. 39, 383–417.CrossRefGoogle Scholar
Kim, J. & Moin, P. 1985 Application of a fractional-step method to incompressible Navier–Stokes equations. J. Comput. Phys. 59, 308–323.CrossRefGoogle Scholar
Kim, J., Moin, P. & Moser, R. 1987 Turbulence statistics in fully developed channel flow at low Reynolds number. J. Fluid Mech. 177, 133–166.Google Scholar
Lasagna, D., Fronges, L., Orazi, M. & Iuso, G. 2015 Nonlinear multi-time-delay stochastic estimation: application to cavity and turbulent channel flow. AIAA J. 53 (10), 2920–2935.Google Scholar
Lasagna, D. & Tutty, O. 2015 Wall-based reduced-order modelling. Intl J. Numer. Meth. Fluids 80 (9), 511–535.Google Scholar
Lumley, J. L. 1970 Stochastic Tool in Turbulence. Academic.Google Scholar
Lyons, S. L., Hanratty, T. J. & McLaughlin, J. B. 1991 Large-scale computer simulation of fully developed turbulent channel flow with heat transfer. Intl J. Numer. Meth. Fluids 13 (8), 999–1028.Google Scholar
Marcus, P. S. 1984 Simulation of Taylor–Couette flow. Part 1. Numerical methods and comparison with experiment. J. Fluid Mech. 146, 45–64.CrossRefGoogle Scholar
Moser, R. D., Kim, J. & Mansour, N. N. 1999 Direct numerical simulation of turbulent channel from up to Re 𝜏 = 590. Phys. Fluids 11 (4), 943–945.Google Scholar
Smith, C. R. & Metzler, S. P. 1983 The characteristics of low-speed streaks in the near-wall region of a turbulent boundary layer. J. Fluid Mech. 129, 27–54.Google Scholar
Suzuki, T. 2012 Reduced-order Kalman-filtered hybrid simulation combining particle tracking velocimetry and direct numerical simulation. J. Fluid Mech. 709, 249–288.CrossRefGoogle Scholar
Suzuki, T., Ji, H. & Yamamoto, F. 2009a Unsteady PTV velocity field past an airfoil solved with DNS: Part 1. Algorithm of hybrid simulation and hybrid velocity field at Re ≈ 103 . Exp. Fluids 47 (6), 957–976.Google Scholar
Suzuki, T., Ji, H. & Yamamoto, F. 2010 Instability waves in a low-Reynolds-number planar jet investigated with hybrid simulation combining particle tracking velocimetry and direct numerical simulation. J. Fluid Mech. 655, 344–379.CrossRefGoogle Scholar
Suzuki, T., Sanse, A., Mizushima, T. & Yamamoto, F. 2009b Unsteady PTV velocity field past an airfoil solved with DNS: Part 2. Validation and application at Reynolds numbers up to Re ≲ 104 . Exp. Fluids 47 (6), 977–994.Google Scholar
Tinney, C. E., Coiffet, F., Delville, J., Hall, A. M., Jordan, P. & Glauser, M. N. 2006 On spectral linear stochastic estimation. Exp. Fluids 41, 763–775.CrossRefGoogle Scholar