Hostname: page-component-78c5997874-ndw9j Total loading time: 0 Render date: 2024-11-17T11:25:22.772Z Has data issue: false hasContentIssue false
  • English
  • Français

Estimating large-scale structures in wall turbulence using linear models

Published online by Cambridge University Press:  06 March 2018

Simon J. Illingworth Open the ORCID record for Simon J. Illingworth [Opens in a new window] ,
Jason P. Monty  and
Ivan Marusic
Simon J. Illingworth*
Affiliation:
Mechanical Engineering, University of Melbourne, VIC 3010, Australia
Jason P. Monty
Affiliation:
Mechanical Engineering, University of Melbourne, VIC 3010, Australia
Ivan Marusic
Affiliation:
Mechanical Engineering, University of Melbourne, VIC 3010, Australia
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

A dynamical systems approach is used to devise a linear estimation tool for channel flow at a friction Reynolds number of 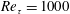$Re_{\unicode[STIX]{x1D70F}}=1000$. The estimator uses time-resolved velocity measurements at a single wall-normal location to estimate the velocity field at other wall-normal locations (the data coming from direct numerical simulations). The estimation tool builds on the work of McKeon & Sharma (J. Fluid Mech., vol. 658, 2010, pp. 336–382) by using a Navier–Stokes-based linear model and treating any nonlinear terms as unknown forcings to an otherwise linear system. In this way nonlinearities are not ignored, but instead treated as an unknown model input. It is shown that, while the linear estimator qualitatively reproduces large-scale flow features, it tends to overpredict the amplitude of velocity fluctuations – particularly for structures that are long in the streamwise direction and thin in the spanwise direction. An alternative linear model is therefore formed in which a simple eddy viscosity is used to model the influence of the small-scale turbulent fluctuations on the large scales of interest. This modification improves the estimator performance significantly. Importantly, as well as improving the performance of the estimator, the linear model with eddy viscosity is also able to predict with reasonable accuracy the range of wavenumber pairs and the range of wall-normal heights over which the estimator will perform well.

JFM classification

Turbulent Flows: Turbulence control Turbulent Flows: Turbulence modelling Turbulent Flows: Turbulent Flows
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 842 , 10 May 2018 , pp. 146 - 162
Check for updates
Copyright
© 2018 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Abe, H., Kawamura, H. & Choi, H. 2004 Very large-scale structures and their effects on the wall shear-stress fluctuations in a turbulent channel flow up to Re 𝜏 = 640. J. Fluids Engng 126 (5), 835–843.CrossRefGoogle Scholar
Adrian, R. J., Meinhart, C. D. & Tomkins, C. D. 2000 Vortex organization in the outer region of the turbulent boundary layer. J. Fluid Mech. 422, 1–54.CrossRefGoogle Scholar
Adrian, R. J. & Moin, P. 1988 Stochastic estimation of organized turbulent structure: homogeneous shear flow. J. Fluid Mech. 190, 531–559.CrossRefGoogle Scholar
del Álamo, J. C. & Jiménez, J. 2006 Linear energy amplification in turbulent channels. J. Fluid Mech. 559, 205–213.CrossRefGoogle Scholar
Andersson, P., Berggren, M. & Henningson, D. S. 1999 Optimal disturbances and bypass transition in boundary layers. Phys. Fluids 11 (1), 134–150.CrossRefGoogle Scholar
Balakumar, B. J. & Adrian, R. J. 2007 Large- and very-large-scale motions in channel and boundary-layer flows. Phil. Trans. R. Soc. Lond. A 365 (1852), 665–681.Google ScholarPubMed
Bamieh, B. & Dahleh, M. 2001 Energy amplification in channel flows with stochastic excitation. Phys. Fluids 13 (11), 3258–3269.CrossRefGoogle Scholar
Berrut, J.-P. & Trefethen, L. N. 2004 Barycentric Lagrange interpolation. SIAM Rev. 46 (3), 501–517.CrossRefGoogle Scholar
Butler, K. M. & Farrell, B. F. 1992 Three-dimensional optimal perturbations in viscous shear flow. Phys. Fluids 4 (8), 1637–1650.CrossRefGoogle Scholar
Cantwell, B. J. 1981 Organized motion in turbulent flow. Annu. Rev. Fluid Mech. 13 (1), 457–515.CrossRefGoogle Scholar
Cess, R. D.1958 A survey of the literature on heat transfer in turbulent tube flow. Tech. Rep. 8-0529-R24, Westinghouse Research.Google Scholar
Chevalier, M., Hœpffner, J., Bewley, T. R. & Henningson, D. S. 2006 State estimation in wall-bounded flow systems. Part 2. Turbulent flows. J. Fluid Mech. 552, 167–187.CrossRefGoogle Scholar
Cossu, C., Pujals, G. & Depardon, S. 2009 Optimal transient growth and very large-scale structures in turbulent boundary layers. J. Fluid Mech. 619, 79–94.CrossRefGoogle Scholar
Doyle, J. C., Glover, K., Khargonekar, P. P. & Francis, B. A. 1989 State-space solutions to standard H2 and H ∞ control problems. IEEE Trans. Automat. Control 34 (8), 831–847.CrossRefGoogle Scholar
Farrell, B. F. & Ioannou, P. J. 1993 Stochastic forcing of the linearized Navier–Stokes equations. Phys. Fluids 5 (11), 2600–2609.CrossRefGoogle Scholar
Farrell, B. F. & Ioannou, P. J. 1996 Generalized stability theory. Part I: autonomous operators. J. Atmos. Sci. 53 (14), 2025–2040.2.0.CO;2>CrossRefGoogle Scholar
Graham, J., Kanov, K., Yang, X. I. A., Lee, M., Malaya, N., Lalescu, C. C., Burns, R., Eyink, G., Szalay, A., Moser, R. D. & Meneveau, C. 2016 A web services accessible database of turbulent channel flow and its use for testing a new integral wall model for LES. J. Turbul. 17 (2), 181–215.CrossRefGoogle Scholar
Guala, M., Hommema, S. E. & Adrian, R. J. 2006 Large-scale and very-large-scale motions in turbulent pipe flow. J. Fluid Mech. 554, 521–542.CrossRefGoogle Scholar
Gustavsson, L. H. 1991 Energy growth of three-dimensional disturbances in plane Poiseuille flow. J. Fluid Mech. 224, 241–260.CrossRefGoogle Scholar
Hœpffner, J., Chevalier, M., Bewley, T. R. & Henningson, D. S. 2005 State estimation in wall-bounded flow systems. Part 1. Perturbed laminar flows. J. Fluid Mech. 534, 263–294.CrossRefGoogle Scholar
Hutchins, N. & Marusic, I. 2007a Evidence of very long meandering features in the logarithmic region of turbulent boundary layers. J. Fluid Mech. 579, 1–28.CrossRefGoogle Scholar
Hutchins, N. & Marusic, I. 2007b Large-scale influences in near-wall turbulence. Phil. Trans. R. Soc. Lond. A 365 (1852), 647–664.Google ScholarPubMed
Hwang, Y. 2016 Mesolayer of attached eddies in turbulent channel flow. Phys. Rev. Fluids 1, 064401.CrossRefGoogle Scholar
Hwang, Y. & Cossu, C. 2010a Amplification of coherent streaks in the turbulent Couette flow: an input–output analysis at low Reynolds number. J. Fluid Mech. 643, 333–348.CrossRefGoogle Scholar
Hwang, Y. & Cossu, C. 2010b Linear non-normal energy amplification of harmonic and stochastic forcing in the turbulent channel flow. J. Fluid Mech. 664, 51–73.CrossRefGoogle Scholar
Jiménez, J. 2012 Cascades in wall-bounded turbulence. Annu. Rev. Fluid Mech. 44, 27–45.CrossRefGoogle Scholar
Jones, B. L., Kerrigan, E. C., Morrison, J. F. & Zaki, T. A. 2011 Flow estimation of boundary layers using DNS-based wall shear information. Intl J. Control 84 (8), 1310–1325.CrossRefGoogle Scholar
Jovanovic, M. R.2004 Modeling, analysis, and control of spatially distributed systems. PhD thesis, University of California at Santa Barbara.Google Scholar
Jovanovic, M. R. & Bamieh, B. 2001 The spatio-temporal impulse response of the linearized Navier–Stokes equations. In Proceedings of the 2001 American Control Conference, vol. 3, pp. 1948–1953.Google Scholar
Jovanovic, M. R. & Bamieh, B. 2005 Componentwise energy amplification in channel flows. J. Fluid Mech. 534, 145–183.CrossRefGoogle Scholar
Kim, K. C. & Adrian, R. J. 1999 Very large-scale motion in the outer layer. Phys. Fluids 11 (2), 417–422.CrossRefGoogle Scholar
Komminaho, J., Lundbladh, A. & Johansson, A. V. 1996 Very large structures in plane turbulent Couette flow. J. Fluid Mech. 320, 259–285.CrossRefGoogle Scholar
Malkus, W. V. R. 1956 Outline of a theory of turbulent shear flow. J. Fluid Mech. 1 (05), 521–539.CrossRefGoogle Scholar
Mathis, R., Hutchins, N. & Marusic, I. 2009 Large-scale amplitude modulation of the small-scale structures in turbulent boundary layers. J. Fluid Mech. 628, 311–337.CrossRefGoogle Scholar
McKeon, B. J. & Sharma, A. S. 2010 A critical-layer framework for turbulent pipe flow. J. Fluid Mech. 658, 336–382.CrossRefGoogle Scholar
McKeon, B. J., Sharma, A. S. & Jacobi, I. 2013 Experimental manipulation of wall turbulence: a systems approach. Phys. Fluids 25 (3), 031301.CrossRefGoogle Scholar
Moarref, R., Jovanović, M. R., Tropp, J. A., Sharma, A. S. & McKeon, B. J. 2014 A low-order decomposition of turbulent channel flow via resolvent analysis and convex optimization. Phys. Fluids 26 (5), 051701.CrossRefGoogle Scholar
Moarref, R., Sharma, A. S., Tropp, J. A. & McKeon, B. J. 2013 Model-based scaling of the streamwise energy density in high-Reynolds-number turbulent channels. J. Fluid Mech. 734, 275–316.CrossRefGoogle Scholar
Monty, J. P., Stewart, J. A., Williams, R. C. & Chong, M. S. 2007 Large-scale features in turbulent pipe and channel flows. J. Fluid Mech. 589, 147–156.CrossRefGoogle Scholar
Pujals, G., García-Villalba, M., Cossu, C. & Depardon, S. 2009 A note on optimal transient growth in turbulent channel flows. Phys. Fluids 21 (1), 015109.CrossRefGoogle Scholar
Reddy, S. C. & Henningson, D. S. 1993 Energy growth in viscous channel flows. J. Fluid Mech. 252, 209–238.CrossRefGoogle Scholar
Reynolds, W. C. & Hussain, A. K. M. F. 1972 The mechanics of an organized wave in turbulent shear flow. Part 3. Theoretical models and comparisons with experiments. J. Fluid Mech. 54 (02), 263–288.CrossRefGoogle Scholar
Reynolds, W. C. & Tiederman, W. G. 1967 Stability of turbulent channel flow, with application to Malkus’s theory. J. Fluid Mech. 27 (2), 253–272.CrossRefGoogle Scholar
Robinson, S. K. 1991 Coherent motions in the turbulent boundary layer. Annu. Rev. Fluid Mech. 23 (1), 601–639.CrossRefGoogle Scholar
Schmid, P. J. 2007 Nonmodal stability theory. Annu. Rev. Fluid Mech. 39 (1), 129–162.CrossRefGoogle Scholar
Schmid, P. J. & Henningson, D. S. 1994 Optimal energy density growth in Hagen–Poiseuille flow. J. Fluid Mech. 277, 197–225.CrossRefGoogle Scholar
Schmid, P. J. & Henningson, D. S. 2001 Stability and Transition in Shear Flows. Springer.CrossRefGoogle Scholar
Seron, M. M., Braslavsky, J. H. & Goodwin, G. C. 2012 Fundamental Limitations in Filtering and Control. Springer.Google Scholar
Sharma, A. S. & McKeon, B. J. 2013 On coherent structure in wall turbulence. J. Fluid Mech. 728, 196–238.CrossRefGoogle Scholar
Smits, A. J., McKeon, B. J. & Marusic, I. 2011 High-Reynolds number wall turbulence. Annu. Rev. Fluid Mech. 43, 353–375.CrossRefGoogle Scholar
Tomkins, C. D. & Adrian, R. J. 2005 Energetic spanwise modes in the logarithmic layer of a turbulent boundary layer. J. Fluid Mech. 545, 141–162.CrossRefGoogle Scholar
Trefethen, L. N., Trefethen, A. E., Reddy, S. C. & Driscoll, T. A. 1993 Hydrodynamic stability without eigenvalues. Science 261 (5121), 578–584.CrossRefGoogle ScholarPubMed
Willis, A. P., Hwang, Y. & Cossu, C. 2010 Optimally amplified large-scale streaks and drag reduction in turbulent pipe flow. Phys. Rev. E 82 (3), 036321.Google ScholarPubMed
Zare, A., Jovanovic, M. R. & Georgiou, T. T. 2017 Colour of turbulence. J. Fluid Mech. 812, 636–680.CrossRefGoogle Scholar
Zhou, K. & Doyle, J. C. 1998 Essentials of Robust Control. Prentice Hall.Google Scholar

Illingworth et al. supplementary movie 1

Estimation of the streamwise velocity perturbation at $z^+=101$ using the linear model \eqref{eq:lm1}: (\textit{a}) DNS data; and (\textit{b}) linear estimate using measurements at $z^+=197$; (\textit{c}) time history at $x=\pi/2$, $y=\pi/2$ for the DNS data (---) and for the linear estimate (-\,-). Sixty-five contour levels are shown from $u=-3.5$ (blue) to $u=+3.5$ (red).

Download Illingworth et al. supplementary movie 1(Video)
Video 56.5 MB

Illingworth et al. supplementary movie 2

Estimation of the streamwise velocity perturbation at $z^+=297$ using the linear model \eqref{eq:lm1}: (\textit{a}) DNS data; and (\textit{b}) linear estimate using measurements at $z^+=197$; (\textit{c}) time history at $x=\pi/2$, $y=\pi/2$ for the DNS data (---) and for the linear estimate (-\,-). Sixty-five contour levels are shown from $u=-3.5$ (blue) to $u=+3.5$ (red).

Download Illingworth et al. supplementary movie 2(Video)
Video 47.9 MB

Illingworth et al. supplementary movie 3

Estimation of the streamwise velocity perturbation at $z^+=101$ using the linear model \eqref{eq:lm2}: (\textit{a}) DNS data; and (\textit{b}) linear estimate using measurements at $z^+=197$; (\textit{c}) time history at $x=\pi/2$, $y=\pi/2$ for the DNS data (---) and for the linear estimate (-\,-). Sixty-five contour levels are shown from $u=-3.5$ (blue) to $u=+3.5$ (red).

Download Illingworth et al. supplementary movie 3(Video)
Video 38.5 MB

Illingworth et al. supplementary movie 4

Estimation of the streamwise velocity perturbation at $z^+=297$ using the linear model \eqref{eq:lm2}: (\textit{a}) DNS data; and (\textit{b}) linear estimate using measurements at $z^+=197$; (\textit{c}) time history at $x=\pi/2$, $y=\pi/2$ for the DNS data (---) and for the linear estimate (-\,-). Sixty-five contour levels are shown from $u=-3.5$ (blue) to $u=+3.5$ (red).

Download Illingworth et al. supplementary movie 4(Video)
Video 29 MB