Hostname: page-component-745bb68f8f-kw2vx Total loading time: 0 Render date: 2025-01-09T21:56:07.224Z Has data issue: false hasContentIssue false
  • English
  • Français

Estimating intermittency in three-dimensional Navier–Stokes turbulence

Published online by Cambridge University Press:  14 April 2009

J. D. GIBBON
J. D. GIBBON*
Affiliation:
Department of Mathematics, Imperial College London, London SW7 2AZ, UK
*
†E-mail address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

The issue of why computational resolution in Navier–Stokes turbulence is hard to achieve is addressed. Under the assumption that the three-dimensional Navier–Stokes equations have a global attractor it is nevertheless shown that solutions can potentially behave differently in two distinct regions of space–time 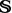± where 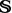− is comprised of a union of disjoint space–time ‘anomalies’. If 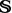− is non-empty it is dominated by large values of |∇ω|, which is consistent with the formation of vortex sheets or tightly coiled filaments. The local number of degrees of freedom 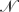± needed to resolve the regions in 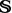± satisfies 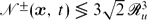, where 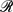u = uL/ν is a Reynolds number dependent on the local velocity field u(x, t).

Type
Papers
Information
Journal of Fluid Mechanics , Volume 625 , 25 April 2009 , pp. 125 - 133
Copyright
Copyright © Cambridge University Press 2009

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

Batchelor, G. K. & Townsend, A. A. 1949 The nature of turbulent flow at large wave-numbers. Proc R. Soc. Lond. A 199, 238–255.Google Scholar
Boffetta, G., Mazzino, A. & Vulpiani, A. 2008 Twenty five years of multifractals in fully developed turbulence: a tribute to Giovanni Paladin. J. Phys. A 41, 363001.Google Scholar
Cadot, O., Douady, S. & Couder, Y. 1995 Characterization of the low-pressure filaments in three-dimensional turbulent shear flow. Phys. Fluids 7, 630–646.CrossRefGoogle Scholar
Caffarelli, L., Kohn, R. & Nirenberg, L. 1982 Partial regularity of suitable weak solutions of the Navier-Stokes equations. Comm. Pure Appl. Math. 35, 771–831.CrossRefGoogle Scholar
Cao, C., & Titi, E. S. 2007 Global well-posedness of the three-dimensional viscous primitive equations of large scale ocean and atmosphere dynamics. Ann. Math. 166, 245–267.CrossRefGoogle Scholar
Cheng, H. 2004 On partial regularity for weak solutions to the Navier–Stokes equations. J. Funct. Anal. 211 (1), 153–162.Google Scholar
Choe, H. J. & Lewis, J. L. 2000 On the singular set in the Navier–Stokes equations. J. Funct. Anal. 175, 348–369.CrossRefGoogle Scholar
Constantin, P. & Foias, C. 1988 Navier–Stokes Equations. University of Chicago Press.CrossRefGoogle Scholar
Doering, C. R. & Foias, C. 2002 Energy dissipation in body-forced turbulence. J. Fluid Mech. 467, 289–306.CrossRefGoogle Scholar
Douady, S., Couder, Y. & Brachet, M. E. 1991 Direct observation of the intermittency of intense vortex filaments in turbulence. Phys. Rev. Letts. 67, 983–986.CrossRefGoogle Scholar
Emmons, H. W. 1951 Laminar–turbulent transition in boundary layers. J. Aero. Sci. 18, 490–498.CrossRefGoogle Scholar
Foias, C., Guillopé, C. & Temam, R. 1981 New a priori estimates for Navier–Stokes equations in dimension 3. Comm. Partial Diff. Eq. 6, 329–359.CrossRefGoogle Scholar
Foias, C., Manley, O., Rosa, R. & Temam, R. 2001 Navier–Stokes Equations & Turbulence. Cambridge University Press.CrossRefGoogle Scholar
Frisch, U. 1995 Turbulence: The legacy of A. N. Kolmogorov. Cambridge University Press.CrossRefGoogle Scholar
Grossmann, S. & Lohse, D. 1993 Intermittency exponents. Europhys. Lett. 21, 201–206.CrossRefGoogle Scholar
Jimenez, J., Wray, A. A., Saffman, P. G. & Rogallo, R. S. 1993 The structure of intense vorticity in isopropic turbulence. J. Fluid Mech. 255, 65–91.CrossRefGoogle Scholar
Kerr, R. M. 1985 Higher order derivative correlations and the alignment of small–scale structures in isotropic numerical turbulence. J. Fluid Mech. 153, 31–58.CrossRefGoogle Scholar
Kerr, R. M. 2001 A new role for vorticity and singular dynamics in turbulence. In Nonlinear Instability Analysis Volume II (ed. Debnath, L.), pp. 15–68. WIT Press.Google Scholar
Kuo, A. Y.-S. & Corrsin, S. 1971 Experiments on internal intermittency and fine-structure distribution functions in fully turbulent fluid. J. Fluid Mech. 50, 285–320.CrossRefGoogle Scholar
Kurien, S. & Taylor, M. 2005 Direct numerical simulation of turbulence: data generation and statistical analysis. Los Alamos Sci. 29, 142–151.Google Scholar
Ladyzhenskaya, O. A. 1963 The Mathematical Theory of Viscous Incompressible Flow. Gordon and Breach.Google Scholar
Ladyzhenskaya, O. & Seregin, G. 1999 On partial regularity of suitable weak solutions of the three dimensional Navier–Stokes equations. St. Petersburg Math. J. 1, 356–387.Google Scholar
Leray, J. 1934 Essai sur le mouvement d'un liquide visquex emplissant l'espace. Acta Math. 63, 193–248.CrossRefGoogle Scholar
Lin, F. 1998 A new proof of the Caffarelli, Kohn & Nirenberg theorem. Comm. Pure Appl. Maths. 51, 241–257.3.0.CO;2-A>CrossRefGoogle Scholar
Madja, A. J. & Bertozzi, A. 2001 Vorticity & Incompressible Flow. Cambridge University Press.Google Scholar
Meneveau, C. & Sreenivasan, K. 1991 The multifractal nature of turbulent energy dissipation. J. Fluid Mech. 224, 429–484.CrossRefGoogle Scholar
Schumacher, J., Sreenivasan, K., & Yakhot, V. 2007 Asymptotic exponents from low-Reynolds-number flows. New J. Phys. 9, 89–108.CrossRefGoogle Scholar
Schumacher, J., Sreenivasan, K. R. & Yeung, P. K. 2005 Very fine structures in scalar mixing. J. Fluid Mech. 531, 113–122.CrossRefGoogle Scholar
Sreenivasan, K. R. 2004 Possible effects of small-scale intermittency in turbulent reacting flows. Flow Turbul. Combust. 72, 115–141.CrossRefGoogle Scholar
Tsinober, A. 1998 Is concentrated vorticity that important? Eur. J. Mech B/Fluids 17, 421–449.CrossRefGoogle Scholar
Tsinober, A. 2000 Vortex stretching versus production of strain/dissipation. In Turbulence Structure & Vortex Dynamics (ed. Hunt, J. & Vassilicos, J.), pp. 164–191. Cambridge University Press.Google Scholar
Tsinober, A. 2001 An Informal Introduction to Turbulence. Kluwer.CrossRefGoogle Scholar
Vincent, A. & Meneguzzi, M. 1994 The dynamics of vorticity tubes of homogeneous turbulence. J. Fluid Mech. 225, 245–254.CrossRefGoogle Scholar
Yakhot, V. 2003 Pressure – velocity correlations and scaling exponents in turbulence. J. Fluid Mech. 495, 135–143.CrossRefGoogle Scholar
Yokokawa, M., Itakura, K., Uno, A., Ishihara, T. & Kaneda, Y. 2002 16.4-Tflops direct numerical simulation of turbulence by a Fourier spectral method on the Earth simulator. In Proceedings of 2002 ACM/IEEE Conference on Supercomputing, Baltimore pp. 1–17. IEEE Computer Society Press.CrossRefGoogle Scholar
Zeff, B. W., Lanterman, D., McAllister, R., Roy, R., Kostelich, E. & Lathrop, D. 2003 Measuring intense rotation & dissipation in turbulent flows. Nature 421, 146–149.CrossRefGoogle ScholarPubMed