Article contents
Erosion–deposition waves in shallow granular free-surface flows
Published online by Cambridge University Press: 02 December 2014
Abstract
Debris flows can spontaneously develop regular large-amplitude surge waves that are interspersed by periods in which the channel fill is completely stationary. These are important because each individual surge is much more destructive than a steady uniform flow with the same mass flux. In this paper small-scale experiments that exhibit similar behaviour are described. The flow consists of carborundum particles that flow down a rough inclined chute covered with a static erodible layer of the same grains. For inflow conditions close to the minimum depth required for steady uniform flows to exist, small disturbances are unstable, creating waves that rapidly coarsen and grow in size. As the waves become sufficiently large, the troughs between the wave crests drop below a critical thickness and come to rest. A series of steadily travelling waves develop which erode the static layer of particles in front of them and deposit grains behind them, to form a layer that is again stationary. This is, in turn, re-eroded and deposited by the next wave. We term these waves granular erosion–deposition waves. Although erosion and deposition problems are notoriously difficult, a simple model is developed which uses a depth-averaged version of the 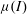 ${\it\mu}(I)$-rheology and Pouliquen and Forterre’s extended friction law. The viscous dissipation combines with dynamic, intermediate and static friction regimes to generate finite-length waves with static and mobile regions. The existence of stationary layers fundamentally distinguishes erosion–deposition waves from granular roll waves, which form in slightly deeper flows and are always completely mobilized. Numerical simulations show that the system of equations is able to model both erosion–deposition waves and granular roll waves. Moreover, the computed wave amplitude, wavespeed and coarsening dynamics are in good quantitative agreement with experiments.
${\it\mu}(I)$-rheology and Pouliquen and Forterre’s extended friction law. The viscous dissipation combines with dynamic, intermediate and static friction regimes to generate finite-length waves with static and mobile regions. The existence of stationary layers fundamentally distinguishes erosion–deposition waves from granular roll waves, which form in slightly deeper flows and are always completely mobilized. Numerical simulations show that the system of equations is able to model both erosion–deposition waves and granular roll waves. Moreover, the computed wave amplitude, wavespeed and coarsening dynamics are in good quantitative agreement with experiments.
- Type
- Papers
- Information
- Copyright
- © 2014 Cambridge University Press
References
Edwards and Gray supplementary movie
An oblique view of erosion-deposition waves propagating from top to bottom in a flow of carborundum particles, on a chute inclined at 35.1 degrees to the horizontal with a rough bed of spherical glass beads. The chute has glass sidewalls on its 7.8cm width and a length of 3.29m from the inflow gate to the outflow end, with a visible region here that is approximately 50cm in length and near to the midpoint of the downslope $x$-direction. Regions of stationary material between successive waves and the merging of waves propagating at different speeds can be observed.
Edwards and Gray supplementary movie
An overhead view of erosion-deposition waves propagating from top to bottom in a flow of carborundum particles, on a chute inclined at 35.1 degrees to the horizontal with a rough bed of spherical glass beads. The chute has glass sidewalls on its 7.8cm width and a length of 3.29m from the inflow gate to the outflow end, with a visible region here that is approximately 0.2m in length and near to the midpoint of the downslope $x$-direction. Regions of stationary material between successive waves and the merging of waves propagating at different speeds can be observed.
Edwards and Gray supplementary movie
A flow of carborundum particles, from left to right, on a chute inclined at 35.1 degrees to the horizontal viewed through the glass sidewalls, with a visible region here that is approximately 16cm in length and near to the midpoint of the downslope $x$-direction, in alignment with the chute to give the flow thickness profile on the vertical axis. The positions of the spherical glass beads which form the rough bed of the chute are visible on the right-hand side as white circles. It is observed that the waves erode at material below the thickness of the initial static uniform layer, but not all the way down to the bed.
Edwards and Gray supplementary movie
Flow thickness $h$ varying with downslope position $x$, obtained from numerical simulations on a periodic domain with travelling-wave solution, shown in figure~\ref{fig9}(a), as the initial conditions and a 2nd-order Runge-Kutta time-stepper. The flow thickness profile is observed to remain unchanged, aside from small variations in the constant thickness $h_{+}$ of the stationary layer, after the given period of time has elapsed. These variations are greater than when a 3rd-order adaptive Runge-Kutta time-stepper is used (movie 3).
Edwards and Gray supplementary movie
Flow thickness $h$ varying with downslope position $x$, obtained from numerical simulations on a periodic domain with travelling-wave solution, shown in figure~\ref{fig9}(a), as the initial conditions and a 3rd-order adaptive Runge-Kutta time-stepper. The flow thickness profile is observed to remain unchanged, aside from small variations in the constant thickness $h_{+}$ of the stationary layer, after the given period of time has elapsed. These variations are smaller than when a 2nd-order Runge-Kutta time-stepper is used (movie 4).
Edwards and Gray supplementary movie
The flow thickness $h$ obtained by a numerical simulation in a periodic domain with initial conditions $h(x,t=0)=h_{\mathrm{stop}} + 10^{-4}H(x)$, where $H(x)\in[-1,1]$ is a zero-mean pseudo-random perturbation to the thickness $h_{\mathrm{stop}}$ of a steady uniform flow. The roll wave instability causes the perturbation to grow and eventually coarsen to form one solitary, steady travelling erosion-deposition wave, along with a region of stationary material, which fills the length of the domain.
Edwards and Gray supplementary movie
Results of a numerical simulation showing the flow thickness $h$ and the depth-averaged velocity $\bar{u}$ with downslope position $x$(m) (solid lines). At the inflow boundary, a flow thickness $h(x=0,t)=h_0 + 10^{-4}H(t)$ is prescribed, where $H(t)=\sin{(2\pi f t)}$ is a sinusoidal perturbation, with $f=0.47$Hz, to a steady uniform flow, of thickness $h_0=h_{\mathrm{stop}}$ and corresponding depth-averaged velocity $\bar{u}_0=\bar{u}_{\mathrm{stop}}$, imposed as an initial condition (dashed lines). Erosion-deposition waves of the inflow frequency, $f=0.47$Hz, grow downslope of the inflow gate and the important experimental flow feature of stationary regions between waves, where $\bar{u}=0$, is captured numerically.
Edwards and Gray supplementary movie
Results of a numerical simulation showing the flow thickness $h$ and the depth-averaged velocity $\bar{u}$ with downslope position $x$(m) (solid lines). At the inflow boundary, a flow thickness $h(x=0,t)=h_0 + 10^{-4}H(t)$ is prescribed, where $H(t)=\sin{(2\pi f t)}$ is a sinusoidal perturbation, with $f=0.47$Hz, to a steady uniform flow, of thickness $h_0=1.2 h_{\mathrm{stop}}$ and corresponding depth-averaged velocity $\bar{u}_0 =(1.2)^{3/2}\bar{u}_{\mathrm{stop}}$, imposed as an initial condition (dashed-dotted lines). The minimum flow thickness and velocity for which a steady uniform flow is possible, $h_{\mathrm{stop}}$ and $\bar{u}_{\mathrm{stop}}$ respectively, are also shown (dashed lines). Continuous roll waves of the inflow frequency, $f=0.47$Hz, grow downslope of the inflow gate.
Edwards and Gray supplementary movie
Results of a numerical simulation showing the flow thickness $h$ and the depth-averaged velocity $\bar{u}$ with downslope position $x$(m) (solid lines). At the inflow boundary, a flow thickness $h(x=0,t)=h_0 + 10^{-4}H(t)$ is prescribed, where $H(t)=\sin{(2\pi f t)}$ is a sinusoidal perturbation, with $f=0.47$Hz, to a steady uniform flow, of thickness $h_0=1.2 h_{\mathrm{stop}}$ and corresponding depth-averaged velocity $\bar{u}_0 =(1.2)^{3/2}\bar{u}_{\mathrm{stop}}$, imposed as an initial condition (dashed-dotted lines). The minimum flow thickness and velocity for which a steady uniform flow is possible, $h_{\mathrm{stop}}$ and $\bar{u}_{\mathrm{stop}}$ respectively, are also shown (dashed lines). Continuous roll waves of the inflow frequency, $f=0.47$Hz, grow downslope of the inflow gate.
Edwards and Gray supplementary movie
Results of a numerical simulation showing the flow thickness $h$ and the depth-averaged velocity $\bar{u}$ with downslope position $x$(m) (solid lines). At the inflow boundary, a flow thickness $h(x=0,t)=h_0 + 10^{-4}H(t)$ is prescribed, where $H(t) \in [-1,1]$ is a zero-mean, pseudo-random perturbation to a steady uniform flow, of thickness $h_0=1.2 h_{\mathrm{stop}}$ and corresponding depth-averaged velocity $\bar{u}_0 = (1.2)^{3/2}\bar{u}_{\mathrm{stop}}$, imposed as an initial condition (dashed-dotted lines). The minimum flow thickness and velocity for which a steady uniform flow is possible, $h_{\mathrm{stop}}$ and $\bar{u}_{\mathrm{stop}}$ respectively, are also shown (dashed lines). Continuous roll waves of a range of frequencies grow downslope of the inflow gate and there are mergers of waves with different characteristics.
- 85
- Cited by



