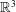Hostname: page-component-78c5997874-4rdpn Total loading time: 0 Render date: 2024-11-04T21:33:20.480Z Has data issue: false hasContentIssue false
  • English
  • Français

Eroding dipoles and vorticity growth for Euler flows in $\mathbb{R}^{3}$: axisymmetric flow without swirl

Published online by Cambridge University Press:  16 September 2016

Stephen Childress ,
Andrew D. Gilbert  and
Paul Valiant
Stephen Childress*
Affiliation:
Courant Institute of Mathematical Sciences, New York University, New York, NY 10012, USA
Andrew D. Gilbert
Affiliation:
Department of Mathematics, University of Exeter, Exeter EX4 4QF, UK
Paul Valiant
Affiliation:
Department of Computer Science, Brown University, Providence, RI 02912, USA
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

A review of analyses based upon anti-parallel vortex structures suggests that structurally stable dipoles with eroding circulation may offer a path to the study of vorticity growth in solutions of Euler’s equations in 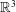$\mathbb{R}^{3}$. We examine here the possible formation of such a structure in axisymmetric flow without swirl, leading to maximal growth of vorticity as 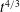$t^{4/3}$. Our study suggests that the optimizing flow giving the $t^{4/3}$ growth mimics an exact solution of Euler’s equations representing an eroding toroidal vortex dipole which locally conserves kinetic energy. The dipole cross-section is a perturbation of the classical Sadovskii dipole having piecewise constant vorticity, which breaks the symmetry of closed streamlines. The structure of this perturbed Sadovskii dipole is analysed asymptotically at large times, and its predicted properties are verified numerically. We also show numerically that if mirror symmetry of the dipole is not imposed but axial symmetry maintained, an instability leads to breakup into smaller vortical structures.

JFM classification

Vortex Flows: Vortex dynamics Vortex Flows: Vortex Flows Vortex Flows: Vortex instability
Type
Papers
Information
Journal of Fluid Mechanics , Volume 805 , 25 October 2016 , pp. 1 - 30
Check for updates
Copyright
© 2016 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Batchelor, G. K. 1956 On steady laminar flow with closed streamlines at large Reynolds number. J. Fluid Mech. 1, 177–190.Google Scholar
Bustamante, M. D. & Kerr, R. M. 2008 3D Euler about a 2D symmetry plane. Physica D 237, 1912–1920.Google Scholar
Carlson, B. C. & Gustafson, J. L. 1985 Asymptotic expansion of the first elliptic integral. SIAM J. Math. Anal. 16, 1072–1092.CrossRefGoogle Scholar
Chernyshenko, S. I. 1988 The asymptotic form of the stationary separated circumfluence of a body at high Reynolds-numbers. PMM J. Appl. Math. Engng 52, 746–753.Google Scholar
Childress, S. 1966 Solutions of Euler’s equations containing finite eddies. Phys. Fluids 9, 860–872.CrossRefGoogle Scholar
Childress, S. 1987 Nearly two-dimensional solutions of Euler’s equations. Phys. Fluids 30, 944–953.Google Scholar
Childress, S. 2008 Growth of anti-parallel vorticity in Euler flows. Physica D 237, 1921–1925.Google Scholar
Childress, S.2009 S. Constraints on stretching by paired vortex structures I. Kinematics, II. The asymptotic dynamics of blow-up in three dimensions. Preliminary reports available at http://www.math.nyu.edu/faculty/childres/preprints.html.Google Scholar
Gibbon, J. D. 2008 The three-dimensional Euler equations: Where do we stand? Physica D 237, 1894–1904.Google Scholar
Grafke, T. & Grauer, R. 2013 Lagrangian and geometric analysis of finite-time Euler singularities. Procedia IUTAM 7, 32–56.Google Scholar
Hormoz, S. & Brenner, M. P. 2012 Absence of singular stretching of interacting vortex filaments. J. Fluid Mech. 707, 191–204.Google Scholar
Hou, T. Y. & Li, R. 2008 Blowup or no blowup? The interplay between theory and numerics. Physica D 237, 1932–1944.Google Scholar
Kerr, R. M. 2013 Bounds on Euler from vorticity moments and line divergence. J. Fluid Mech. 729, R2.CrossRefGoogle Scholar
Lim, T. T. & Nickels, T. B. 1992 Instability and reconnection in the head-on collision of two vortex rings. Nature 357, 225–227.CrossRefGoogle Scholar
Lu, L. & Doering, C. R. 2008 Limits on enstrophy growth for solutions of the three-dimensional Navier–Stokes equations. Indiana Univ. Math. J. 57, 2693–2727.Google Scholar
Luo, G. & Hou, T. Y. 2014 Potentially singular solutions of the 3D axisymmetric Euler equations. Proc. Natl Acad. Sci. USA 111, 12968–12973.Google Scholar
Majda, A. J. & Bertozzi, A. L. 2001 Vorticity and Incompressible Flow. Cambridge University Press.Google Scholar
Meleshko, V. V. & van Heijst, G. J. F. 1994 On Chaplygins investigations of two-dimensional vortex structures in an inviscid fluid. J. Fluid Mech. 272, 157–182.Google Scholar
Moore, D. W., Saffman, P. G. & Tanveer, S. 1988 The calculation of some Batchelor flows: the Sadovskii vortex and rotational corner flow. Phys. Fluids 31, 978–990.Google Scholar
Oshima, Y. 1978 Head-on collision of two vortex rings. J. Phys. Soc. Japan 44, 329–331.Google Scholar
Pierrehumbert, R. T. 1980 A family of steady, translating vortex pairs with distributed vorticity. J. Fluid Mech. 99, 129–144.Google Scholar
Prandtl, L. 1952 Essentials of Fluid Mechanics. Blackie.Google Scholar
Pumir, A. & Kerr, R. M. 1987 Numerical simulation of interacting vortex tubes. Phys. Rev. Lett. 58, 1636–1639.Google Scholar
Pumir, A. & Siggia, E. 1987 Vortex dynamics and the existence of solutions to the Navier–Stokes equations. Phys. Fluids 30, 1606–1626.CrossRefGoogle Scholar
Riley, N. 1998 The fascination of vortex rings. Appl. Sci. Res. 58, 169–189.Google Scholar
Sadovskii, V. S. 1971 Vortex regions in a potential stream with a jump of Bernoulli’s constant at the boundary. Prikl. Mat. Mekh. 35, 773–779.Google Scholar
Saffman, P. G. & Tanveer, S. 1982 The touching pair of equal and opposite vortices. Phys. Fluids 25, 1929–1930.Google Scholar
Shariff, K., Leonard, A. & Ferziger, J. H. 2008 A contour dynamics algorithm for axisymmetric flows. J. Comput. Phys. 227, 9044–9062.Google Scholar
Shelley, M. J., Meiron, D. I. & Orszag, S. A. 1993 Dynamical aspects of vortex reconnection of perturbed anti-parallel vortex tubes. J. Fluid Mech. 246, 613–652.CrossRefGoogle Scholar