Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Pähtz, Thomas
Clark, Abram H.
Valyrakis, Manousos
and
Durán, Orencio
2020.
The Physics of Sediment Transport Initiation, Cessation, and Entrainment Across Aeolian and Fluvial Environments.
Reviews of Geophysics,
Vol. 58,
Issue. 1,
Guerrero, Byron
Lambert, Martin F.
and
Chin, Rey C.
2020.
Extreme wall shear stress events in turbulent pipe flows: spatial characteristics of coherent motions.
Journal of Fluid Mechanics,
Vol. 904,
Issue. ,
Bristow, Nathaniel R.
Blois, Gianluca
Best, James L.
and
Christensen, Kenneth T.
2021.
Unsteady dynamics of turbulent flow in the wakes of barchan dunes modulated by overlying boundary-layer structure.
Journal of Fluid Mechanics,
Vol. 920,
Issue. ,
Fu, Lin-Tao
2021.
Grain size ratio may be crucial for the fluid initiation of martian sand grains.
Icarus,
Vol. 358,
Issue. ,
p.
114225.
Yang, Xiang I. A.
Hong, Jiarong
Lee, Myoungkyu
and
Huang, Xinyi L. D.
2021.
Grid resolution requirement for resolving rare and high intensity wall-shear stress events in direct numerical simulations.
Physical Review Fluids,
Vol. 6,
Issue. 5,
Pähtz, Thomas
Liu, Yonghui
Xia, Yuezhang
Hu, Peng
He, Zhiguo
and
Tholen, Katharina
2021.
Unified Model of Sediment Transport Threshold and Rate Across Weak and Intense Subaqueous Bedload, Windblown Sand, and Windblown Snow.
Journal of Geophysical Research: Earth Surface,
Vol. 126,
Issue. 4,
Jia, Shuming
and
Wang, Zhengshi
2021.
Simulation of aerodynamic entrainment with interparticle cohesions based on discrete element method.
Earth Surface Processes and Landforms,
Vol. 46,
Issue. 7,
p.
1410.
AlObaidi, Khaldoon
and
Valyrakis, Manousos
2021.
Linking the explicit probability of entrainment of instrumented particles to flow hydrodynamics.
Earth Surface Processes and Landforms,
Vol. 46,
Issue. 12,
p.
2448.
Yücesan, Sencer
Wildt, Daniel
Gmeiner, Philipp
Schobesberger, Johannes
Hauer, Christoph
Sindelar, Christine
Habersack, Helmut
and
Tritthart, Michael
2021.
Interaction of Very Large Scale Motion of Coherent Structures with Sediment Particle Exposure.
Water,
Vol. 13,
Issue. 3,
p.
248.
Zheng, Xiaojing
Wang, Guohua
and
Zhu, Wei
2021.
Experimental study on the effects of particle–wall interactions on VLSM in sand-laden flows.
Journal of Fluid Mechanics,
Vol. 914,
Issue. ,
Baker, Lucia J.
and
Coletti, Filippo
2021.
Particle–fluid–wall interaction of inertial spherical particles in a turbulent boundary layer.
Journal of Fluid Mechanics,
Vol. 908,
Issue. ,
Scherer, Markus
Uhlmann, Markus
Kidanemariam, Aman G.
and
Krayer, Michael
2022.
On the role of turbulent large-scale streaks in generating sediment ridges.
Journal of Fluid Mechanics,
Vol. 930,
Issue. ,
Bhat, Aamer Majid
and
Ahanger, Manzoor Ahmad
2022.
Study of Movability Number as the parameter of threshold of sediment motion.
Modeling Earth Systems and Environment,
Vol. 8,
Issue. 1,
p.
639.
Baker, Mariah M.
Newman, Claire E.
Sullivan, Robert
Minitti, Michelle E.
Edgett, Kenneth S.
Fey, Deirdra
Ellison, Doug
and
Lewis, Kevin W.
2022.
Diurnal Variability in Aeolian Sediment Transport at Gale Crater, Mars.
Journal of Geophysical Research: Planets,
Vol. 127,
Issue. 2,
Alhusban, Zaid
and
Valyrakis, Manousos
2022.
Assessing sediment transport dynamics from energy perspective by using the instrumented particle.
International Journal of Sediment Research,
Vol. 37,
Issue. 6,
p.
833.
Franca, Mário J.
Valero, Daniel
and
Liu, Xiaofeng
2022.
Treatise on Geomorphology.
p.
151.
Bristow, Nathaniel R.
2022.
Treatise on Geomorphology.
p.
4.
Li, Yilan
Zhu, Zhenduo
Soong, David T.
Khorasani, Hamed
Wang, Shu
Fitzpatrick, Faith
and
Garcia, Marcelo H.
2022.
FluOil: A Novel Tool for Modeling the Transport of Oil-Particle Aggregates in Inland Waterways.
Frontiers in Water,
Vol. 3,
Issue. ,
Demiral, Dila
Albayrak, Ismail
Turowski, Jens M.
and
Boes, Robert M.
2022.
Particle saltation trajectories in supercritical open channel flows: Roughness effect.
Earth Surface Processes and Landforms,
Vol. 47,
Issue. 15,
p.
3588.
Gold, Thomas
Reiterer, Kevin
Hauer, Christoph
Habersack, Helmut
and
Sindelar, Christine
2023.
Flushing Efficiency of Run-of-River Hydropower Plants: Novel Approaches Based on Physical Laboratory Experiments.
Water,
Vol. 15,
Issue. 14,
p.
2657.
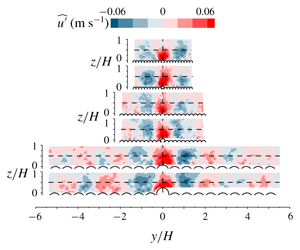
 $1/60~\text{s}^{-1}$. These protrusions were established from extensive initial experiments which utilised an automated mechanism to place spheres on the bed of the flume and record the time elapsed until they were entrained by the flow. The results showed that at lower flow depth to particle diameter ratios, bed particles are more stable and require larger protrusions to entrain at the same rate as at a larger depth. This effect is consistent with observations of reduced velocity variance and reduced drag force variance for lower flow submergences. The PIV measurements indicated that particle entrainment is associated with very large-scale motions which extend up to 50 flow depths in the streamwise direction. Contributions of smaller scale velocity and pressure spatial fluctuations are suppressed by a spatial averaging effect related to the particle size, and a temporal averaging effect related to the time taken to fully entrain a particle from its resting pocket. These observations are relevant to sediment transport modelling. However, further data are required to clarify the role of particle lift forces and particle shape in the entrainment process.
$1/60~\text{s}^{-1}$. These protrusions were established from extensive initial experiments which utilised an automated mechanism to place spheres on the bed of the flume and record the time elapsed until they were entrained by the flow. The results showed that at lower flow depth to particle diameter ratios, bed particles are more stable and require larger protrusions to entrain at the same rate as at a larger depth. This effect is consistent with observations of reduced velocity variance and reduced drag force variance for lower flow submergences. The PIV measurements indicated that particle entrainment is associated with very large-scale motions which extend up to 50 flow depths in the streamwise direction. Contributions of smaller scale velocity and pressure spatial fluctuations are suppressed by a spatial averaging effect related to the particle size, and a temporal averaging effect related to the time taken to fully entrain a particle from its resting pocket. These observations are relevant to sediment transport modelling. However, further data are required to clarify the role of particle lift forces and particle shape in the entrainment process.

