Hostname: page-component-745bb68f8f-b95js Total loading time: 0 Render date: 2025-01-25T06:05:26.717Z Has data issue: false hasContentIssue false
  • English
  • Français

Entrainment at multi-scales across the turbulent/non-turbulent interface in an axisymmetric jet

Published online by Cambridge University Press:  10 August 2016

Dhiren Mistry ,
Jimmy Philip ,
James R. Dawson  and
Ivan Marusic
Dhiren Mistry*
Affiliation:
Department of Engineering, University of Cambridge, Cambridge CB2 1PZ, UK Department of Energy and Process Engineering, Norwegian University of Science and Technology, N-7491 Trondheim, Norway
Jimmy Philip
Affiliation:
Department of Mechanical Engineering, University of Melbourne, Parkville, VIC 3010, Australia
James R. Dawson
Affiliation:
Department of Energy and Process Engineering, Norwegian University of Science and Technology, N-7491 Trondheim, Norway
Ivan Marusic
Affiliation:
Department of Mechanical Engineering, University of Melbourne, Parkville, VIC 3010, Australia
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We consider the scaling of the mass flux and entrainment velocity across the turbulent/non-turbulent interface (TNTI) in the far field of an axisymmetric jet at high Reynolds number. Time-resolved, simultaneous multi-scale particle image velocimetry (PIV) and planar laser-induced fluorescence (PLIF) are used to identify and track the TNTI, and directly measure the local entrainment velocity along it. 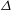Application of box-counting and spatial-filtering methods, with filter sizes $\unicode[STIX]{x1D6E5}$ spanning over two decades in length, show that the mean length of the TNTI exhibits a power-law behaviour with a fractal dimension 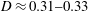$D\approx 0.31{-}0.33$. More importantly, we invoke a multi-scale methodology to confirm that the mean mass flux, which is equal to the product of the entrainment velocity and the surface area, remains constant across the range of filter sizes. The results, within experimental uncertainty, also show that the entrainment velocity along the TNTI exhibits a power-law behaviour with 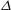$\unicode[STIX]{x1D6E5}$, such that the entrainment velocity increases with increasing 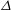$\unicode[STIX]{x1D6E5}$. In fact, the mean entrainment velocity scales at a rate that balances the scaling of the TNTI length such that the mass flux remains independent of the coarse-grain filter size, as first suggested by Meneveau & Sreenivasan (Phys. Rev. A, vol. 41, no. 4, 1990, pp. 2246–2248). Hence, at the smallest scales the entrainment velocity is small but is balanced by the presence of a very large surface area, whilst at the largest scales the entrainment velocity is large but is balanced by a smaller (smoother) surface area.

JFM classification

Wakes/Jets: Jets Turbulent Flows: Turbulent Flows Wakes/Jets: Wakes/Jets
Type
Papers
Information
Journal of Fluid Mechanics , Volume 802 , 10 September 2016 , pp. 690 - 725
Check for updates
Copyright
© 2016 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Aanen, L.2002 Measurement of turbulent scalar mixing by means of a combination of PIV and LIF. PhD thesis, Delft University of Technology.Google Scholar
Adrian, R. J., Meinhart, C. D. & Tomkins, C. D. 2000 Vortex organization in the outer region of the turbulent boundary layer. J. Fluid Mech. 422, 1–54.CrossRefGoogle Scholar
Bisset, D. K., Hunt, J. C. R. & Rogers, M. M. 2002 The turbulent/non-turbulent interface bounding a far wake. J. Fluid Mech. 451, 383–410.CrossRefGoogle Scholar
Brown, G. & Roshko, A. 1974 On density effects and large structure in turbulent mixing layers. J. Fluid Mech. 64 (4), 775–816.Google Scholar
Carazzo, G., Kaminski, E. & Tait, S. 2006 The route to self-similarity in turbulent jets and plumes. J. Fluid Mech. 547, 137–148.CrossRefGoogle Scholar
Catrakis, H. J. 2000 Distribution of scales in turbulence. Phys. Rev. E 62 (1), 564–578.Google Scholar
Catrakis, H. J. & Dimotakis, P. E. 1996 Mixing in turbulent jets: scalar measures and isosurface geometry. J. Fluid Mech. 317, 369–406.CrossRefGoogle Scholar
Chauhan, K., Philip, J. & Marusic, I. 2014a Scaling of the turbulent/non-turbulent interface in boundary layers. J. Fluid Mech. 751, 298–328.Google Scholar
Chauhan, K., Philip, J., de Silva, C., Hutchins, N. & Marusic, I. 2014b The turbulent/non-turbulent interface and entrainment in a boundary layer. J. Fluid Mech. 742, 119–151.Google Scholar
Corrsin, S. & Kistler, A.1955 Free-stream boundaries of turbulent flows Tech. Rep. TN -1244. NASA, Baltimore.Google Scholar
Craske, J. & van Reeuwijk, M. 2015 Energy dispersion in turbulent jets. Part 1. Direct simulation of steady and unsteady jets. J. Fluid Mech. 763, 500–537.Google Scholar
Crimaldi, J. P. 2008 Planar laser induced fluorescence in aqueous flows. Exp. Fluids 44, 851–863.Google Scholar
Dahm, W. J. A. & Dimotakis, P. E. 1987 Measurements of entrainment and mixing in turbulent jets. AIAA J. 25 (9), 1216–1223.Google Scholar
Dimotakis, P. & Catrakis, H. 1999 Turbulence, fractals, and mixing. In Mixing: Chaos and Turbulence (ed. Chaté, H., Villermaux, E. & Chomaz, J. M.). Kluwer Academic/Plenum.Google Scholar
Eisma, J., Westerweel, J., Ooms, G. & Elsinga, G. E. 2015 Interfaces and internal layers in a turbulent boundary layer. Phys. Fluids 27, 055103.Google Scholar
Fischer, H., List, J., Koh, R., Imberger, J. & Brooks, N. 1979 Mixing in Inland and Coastal Waters. Academic.Google Scholar
Fukushima, C., Aanen, L. & Westerweel, J. 2002 Investigation of the mixing process in an axisymmetric turbulent jet using PIV and LIF. In Laser Techniques for Fluid Mechanics, pp. 339–356. Springer.Google Scholar
Gampert, M., Boschung, J., Hennig, F., Gauding, M. & Peters, N. 2014 The vorticity versus the scalar criterion for the detection of the turbulent/non-turbulent interface. J. Fluid Mech. 750, 578–596.Google Scholar
Holzner, M., Liberzon, A., Nikitin, N., Kinzelbach, W. & Tsinober, A. 2007 Small-scale aspects of flows in proximity of the turbulent/nonturbulent interface. Phys. Fluids 19, 071702.Google Scholar
Holzner, M. & Lüthi, B. 2011 Laminar superlayer at the turbulence boundary. Phys. Rev. Lett. 106, 134503.Google Scholar
Hunt, J. C. R., Eames, I. & Westerweel, J. 2014 Vortical interactions with interfacial shear layers. In Proc. IUTAM Symp. on Computational Physics and New Perspectives in Turbulence, vol. 92, pp. 607–649.Google Scholar
Hussein, H. J., Capp, S. P. & George, W. K. 1994 Velocity measurements in a high-Reynolds-number, momentum-conserving, axisymmetric, turbulent jet. J. Fluid Mech. 258, 31–75.Google Scholar
Kaminski, E., Tait, S. & Carazzo, G. 2005 Turbulent entrainment in jets with arbitrary buoyancy. J. Fluid Mech. 526, 361–376.Google Scholar
Krug, D., Holzner, M., Lüthi, B., Wolf, M., Kinzelbach, W. & Tsinober, A. 2015 The turbulent/non-turbulent interface in an inclined dense gravity current. J. Fluid Mech. 765, 303–324.Google Scholar
Liepmann, D. & Gharib, M. 1992 The role of streamwise vorticity in the near-field entrainment of round jets. J. Fluid Mech. 245, 643–668.CrossRefGoogle Scholar
Lubbers, C. L., Brethouwer, G. & Boersma, B. J. 2001 Simulation of the mixing of a passive scalar in a round turbulent jet. Fluid Dyn. Res. 28 (3), 189–208.Google Scholar
Mandelbrot, B. B. 1982 The Fractal Geometry of Nature. W. H. Freeman and Company.Google Scholar
Mathew, J. & Basu, A. 2002 Some characteristics of entrainment at a cylindrical turbulence boundary. Phys. Fluids 14 (7), 2065–2072.CrossRefGoogle Scholar
Meneveau, C. & Sreenivasan, K. R. 1990 Interface dimension in intermittent turbulence. Phys. Rev. A 41 (4), 2246–2248.Google Scholar
Miller, P. L. & Dimotakis, P. E. 1991 Stochastic geometric properties of scalar interfaces in turbulent jets. Phys. Fluids A 3 (1), 168–177.Google Scholar
Morton, B. R., Taylor, G. I. & Turner, J. S. 1956 Turbulent gravitational convection from maintained and instantaneous sources. Proc. R. Soc. Lond. A 234, 1–23.Google Scholar
Moser, R., Rogers, M. & Ewing, D. 1998 Self-similarity of time-evolving plane wakes. J. Fluid Mech. 367, 255–298.Google Scholar
Nickels, T. B. & Marusic, I. 2001 On the different contributions of coherent structures to the spectra of a turbulent round jet and a turbulent boundary layer. J. Fluid Mech. 448, 367–385.CrossRefGoogle Scholar
Panchapakesan, N. & Lumley, J. L. 1993 Turbulence measurements in axisymmetric jets of air and helium. Part 1. Air jet. J. Fluid Mech. 246, 197–223.Google Scholar
Papoulis, A 1991 Probability, Random Variables, and Stochastic Processes. McGraw Hill.Google Scholar
Philip, J. & Marusic, I. 2012 Large-scale eddies and their role in entrainment in turbulent jets and wakes. Phys. Fluids 35, 055108.Google Scholar
Philip, J., Meneveau, C., da Silva, C. & Marusic, I. 2014 Multiscale analysis of fluxes at the turbulent/non-turbulent interface in high Reynolds number boundary layers. Phys. Fluids 26, 015105.CrossRefGoogle Scholar
Poelma, C., Westerweel, J. & Ooms, G. 2006 Turbulence statistics from optical whole-field measurements in particle-laden turbulence. Exp. Fluids 40, 347–363.Google Scholar
Pope, S. B. 2000 Turbulent Flows. Cambridge University Press.Google Scholar
Prasad, R. R. & Sreenivasan, K. R. 1989 Scalar interfaces in digital images of turbulent flows. Exp. Fluids 7, 259–264.Google Scholar
Priestley, C. H. B. & Ball, F. K. 1955 Continuous convection from an isolated source of heat. Q. J. R. Meteorol. Soc. 81 (348), 144–157.Google Scholar
van Reeuwijk, M. & Holzner, M. 2014 The turbulence boundary of a temporal jet. J. Fluid Mech. 739, 254–275.CrossRefGoogle Scholar
Sandham, N. D., Mungal, M. G., Broadwell, J. E. & Reynolds, W. C. 1988 Scalar entrainment in the mixing scalar. In Proceedings of the CTR Summer Program, pp. 69–76.Google Scholar
da Silva, C. & Pereira, J. 2008 Invariants of the velocity-gradient, rate-of-strain, and rate-of-rotation tensors across the turbulent/nonturbulent interface in jets. Phys. Fluids 20, 055101.Google Scholar
da Silva, C. & Taveira, R. 2010 The thickness of the turbulent/nonturbulent interface is equal to the radius of the large vorticity structures near the edge of the shear layer. Phys. Fluids 22, 121702.Google Scholar
da Silva, C., Taveira, R. & Borrell, G. 2014 Characteristics of the turbulent/nonturbulent interface in boundary layers, jets and shear-free turbulence. J. Phys.: Conf. Ser. 506 (1), 012015.Google Scholar
de Silva, C. M., Philip, J., Chauhan, K., Meneveau, C. & Marusic, I. 2013 Multiscale geometry and scaling of the turbulent-nonturbulent interface in high Reynolds number boundary layers. Phys. Rev. Lett. 111, 044501.Google Scholar
Sreenivasan, K. R. 1991 Fractals and multifractals in fluid turbulence. Annu. Rev. Fluid Mech. 23, 539–600.Google Scholar
Sreenivasan, K. R. & Meneveau, C. 1986 The fractal facets of turbulence. J. Fluid Mech. 173, 357–386.Google Scholar
Sreenivasan, K. R. & Prasad, R. R. 1989 New results on the fractal and multifractal structure of the large Schmidt number passive scalars in fully turbulent flows. Physica D 38, 322–329.Google Scholar
Sreenivasan, K. R., Ramshankar, R. & Meneveau, C. 1989 Mixing, entrainment and fractal dimensions of surfaces in turbulent flows. Proc. R. Soc. Lond. 421, 79–108.Google Scholar
Taveira, R. R., Diogo, J. S., Lopes, D. C. & da Silva, C. B. 2013 Lagrangian statistics across the turbulent-nonturbulent interface in a turbulent plane jet. Phys. Rev. E 88, 043001.Google Scholar
Taveira, R. R. & da Silva, C. B. 2014 Characteristics of the viscous superlayer in shear free turbulence and in planar turbulent jets. Phys. Fluids 26, 021702.Google Scholar
Townsend, A. A. 1976 The Structure of Turbulent Shear Flow. Cambridge University Press.Google Scholar
Turner, J. S. 1986 Turbulent entrainment: the development of the entrainment assumption, and its application to geophysical flows. J. Fluid Mech. 173, 431–471.Google Scholar
Westerweel, J., Fukushima, C., Pedersen, J. & Hunt, J. C. R. 2005 Mechanics of the turbulent-nonturbulent interface of a jet. Phys. Rev. Lett. 95, 174501.Google Scholar
Westerweel, J., Fukushima, C., Pedersen, J. & Hunt, J. C. R. 2009 Momentum and scalar transport at the turbulent/non-turbulent interface of a jet. J. Fluid Mech. 631, 199–230.Google Scholar
Westerweel, J., Hofmann, T., Fukushima, C. & Hunt, J. C. R. 2002 The turbulent/non-turbulent interface at the outer boundary of a self-similar turbulent jet. Exp. Fluids 33, 873–878.Google Scholar
Wolf, M., Holzner, M., Lüthi, B., Krug, D., Kinzelbach, W. & Tsinober, A. 2013 Effects of mean shear on the local turbulent entrainment process. J. Fluid Mech. 731, 95–116.CrossRefGoogle Scholar
Wolf, M., Lüthi, B., Holzner, M., Krug, D., Kinzelbach, W. & Tsinober, A. 2012 Investigations on the local entrainment velocity in a turbulent jet. Phys. Fluids 24, 105110.CrossRefGoogle Scholar
Zubair, F. R. & Catrakis, H. J. 2009 On separated shear layers and the fractal geometry of turbulent scalar interfaces at large Reynolds numbers. J. Fluid Mech. 624, 389–411.Google Scholar