Hostname: page-component-78c5997874-j824f Total loading time: 0 Render date: 2024-11-19T08:46:45.978Z Has data issue: false hasContentIssue false
  • English
  • Français

Entraining gravity currents

Published online by Cambridge University Press:  19 August 2013

Christopher G. Johnson  and
Andrew J. Hogg
Christopher G. Johnson*
Affiliation:
Department of Mathematics, University of Bristol, Bristol BS8 1TW, UK
Andrew J. Hogg
Affiliation:
Department of Mathematics, University of Bristol, Bristol BS8 1TW, UK
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Entrainment of ambient fluid into a gravity current, while often negligible in laboratory-scale flows, may become increasingly significant in large-scale natural flows. We present a theoretical study of the effect of this entrainment by augmenting a shallow water model for gravity currents under a deep ambient with a simple empirical model for entrainment, based on experimental measurements of the fluid entrainment rate as a function of the bulk Richardson number. By analysing long-time similarity solutions of the model, we find that the decrease in entrainment coefficient at large Richardson number, due to the suppression of turbulent mixing by stable stratification, qualitatively affects the structure and growth rate of the solutions, compared to currents in which the entrainment is taken to be constant or negligible. In particular, mixing is most significant close to the front of the currents, leading to flows that are more dilute, deeper and slower than their non-entraining counterparts. The long-time solution of an inviscid entraining gravity current generated by a lock-release of dense fluid is a similarity solution of the second kind, in which the current grows as a power of time that is dependent on the form of the entrainment law. 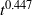With an entrainment law that fits the experimental measurements well, the length of currents in this entraining inviscid regime grows with time approximately as ${t}^{0. 447} $. For currents instigated by a constant buoyancy flux, a different solution structure exists in which the current length grows as 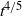${t}^{4/ 5} $. In both cases, entrainment is most significant close to the current front.

JFM classification

Geophysical and Geological Flows: Gravity currents Geophysical and Geological Flows: Shallow water flows
Type
Papers
Information
Journal of Fluid Mechanics , Volume 731 , 25 September 2013 , pp. 477 - 508
Copyright
©2013 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Arita, M. & Jirka, G. H. 1987 Two-layer model of saline wedge I: entrainment and interfacial friction. J. Hydraul. Engng 113, 1229–1247.Google Scholar
Baines, P. G. 2001 Mixing in flows down gentle slopes into stratified environments. J. Fluid Mech. 443, 237–270.Google Scholar
Barenblatt, G. I. 1996 Scaling, Self-similarity, and Intermediate Asymptotics. Cambridge University Press.Google Scholar
Benjamin, T. B. 1968 Gravity currents and related phenomena. J. Fluid Mech. 31, 209–248.Google Scholar
Bonnecaze, R. T. & Lister, J. R. 1999 Particle-driven gravity currents down planar slopes. J. Fluid Mech. 390, 75–91.Google Scholar
Britter, R. E. & Linden, P. F. 1980 The motion of the front of a gravity current travelling down an incline. J. Fluid Mech. 99, 531–543.Google Scholar
Britter, R. E. & Simpson, J. E. 1978 Experiments on the dynamics of a gravity current head. J. Fluid Mech. 88, 223–240.Google Scholar
Christodoulou, G. C. 1986 Interfacial mixing in stratified flows. J. Hydraul Res. 24 (2), 77–92.Google Scholar
Dade, W. B. & Huppert, H. E. 1995 A box model for non-entraining, suspension-driven gravity surges on horizontal surfaces. Sedimentology 42 (3), 453–470.Google Scholar
Ellison, T. H. & Turner, J. S. 1959 Turbulent entrainment in stratified flows. J. Fluid Mech. 6, 423–448.Google Scholar
Fernandez, R. L. & Imberger, J. 2006 Bed roughness induced entrainment in a high Richardson number underflow. J. Hydraul Res. 44 (6), 725–738.Google Scholar
Fernando, H. J. S. 1991 Turbulent mixing in stratified fluids. Annu. Rev. Fluid Mech. 23, 455–493.Google Scholar
Gratton, J. & Vigo, C. 1994 Self-similar gravity currents with variable inflow revisited: plane currents. J. Fluid Mech. 258, 77–104.Google Scholar
Hacker, J., Linden, P. F. & Dalziel, S. B. 1996 Mixing in lock-release gravity currents. Dyn. Atmos. Oceans 24 (1), 183–195.Google Scholar
Hallworth, M. A., Huppert, H. E., Phillips, J. C. & Sparks, R. S. J. 1996 Entrainment into two-dimensional and axisymmetric turbulent gravity currents. J. Fluid Mech. 308, 289–311.Google Scholar
Harris, T. C., Hogg, A. J. & Huppert, H. E. 2001 A mathematical framework for the analysis of particle-driven gravity currents. Proc. R. Soc. A 457, 1241–1272.Google Scholar
Hogg, A. J. 2006 Lock-release gravity currents and dam-break flows. J. Fluid Mech. 569, 61–87.Google Scholar
Hogg, A. J., Hallworth, M. A. & Huppert, H. E. 2005 On gravity currents driven by constant fluxes of saline and particle-laden fluid in the presence of a uniform flow. J. Fluid Mech. 539, 349–385.Google Scholar
Hogg, A. J. & Pritchard, D. 2004 The effects of hydraulic resistance on dam-break and other shallow inertial flows. J. Fluid Mech. 501, 179–212.Google Scholar
Hogg, A. J., Ungarish, M & Huppert, H. E. 2000 Particle-driven gravity currents: asymptotic and box-model solutions. Eur. J. Mech. (B/ Fluids) 338, 139–165.CrossRefGoogle Scholar
Hogg, A. J. & Woods, A. W. 2001 The transition from inertia to bottom-drag-dominated motion of turbulent gravity currents. J. Fluid Mech. 449, 201–224.Google Scholar
Hoult, D. P. 1972 Oil spreading on the sea. Annu. Rev. Fluid Mech. 4, 341–368.Google Scholar
Huppert, H. E. 1982 The propagation of two-dimensional and axisymmetric viscous gravity currents over a rigid horizontal surface. J. Fluid Mech. 121, 43–58.Google Scholar
Huppert, H. E. & Simpson, J. E. 1980 The slumping of gravity currents. J. Fluid Mech. 99, 785–799.CrossRefGoogle Scholar
Kurganov, A. & Tadmor, E. 2000 New high-resolution central schemes for nonlinear conservation laws and convection–diffusion equations. J. Comput. Phys. 160, 241–282.Google Scholar
LeVeque, R. J. 2002 Finite Volume Methods for Hyperbolic Problems. Cambridge University Press.Google Scholar
Marino, B. M., Thomas, L. P. & Linden, P. F. 2005 The front condition for gravity currents. J. Fluid Mech. 536, 49–78.Google Scholar
Mathunjwa, J. S. & Hogg, A. J. 2006 Stability of gravity currents generated by finite volume releases. J. Fluid Mech. 562, 261–278.Google Scholar
Morton, B. R., Taylor, G. & Turner, J. S. 1956 Turbulent gravitational convection from maintained and instantaneous sources. Proc. R. Soc. A 234 (1196), 1–23.Google Scholar
Parker, G., Fukushima, Y. & Pantin, H. M. 1986 Self-accelerating turbidity currents. J. Fluid Mech. 171, 145–181.Google Scholar
Parker, G., Garcia, M., Fukushima, Y. & Yu, W. 1987 Experiments on turbidity currents over an erodible bed. J. Hydraul Res. 25 (1), 123–147.Google Scholar
Ross, A. N., Dalziel, S. B. & Linden, P. F. 2006 Axisymmetric gravity currents on a cone. J. Fluid Mech. 565, 227–254.Google Scholar
Rottman, J. W. & Simpson, J. E. 1983 Gravity currents produced by instantaneous releases of a heavy fluid in a rectangular channel. J. Fluid Mech. 135, 95–110.Google Scholar
Sherman, F. S., Imberger, J. & Corcos, G. M. 1978 Turbulence and mixing in stably stratified waters. Annu. Rev. Fluid Mech. 10, 267–288.Google Scholar
Shin, J. O., Dalziel, S. B. & Linden, P. F. 2004 Gravity currents produced by lock exchange. J. Fluid Mech. 521, 1–34.Google Scholar
Simpson, J. E. 1999 Gravity Currents in the Environment and the Laboratory. Cambridge University Press.Google Scholar
Simpson, J. E. & Britter, R. E. 1979 The dynamics of the head of a gravity current advancing over a horizontal surface. J. Fluid Mech. 94, 477–495.Google Scholar
Sorgard, E. 1991 A numerical, three-layered, stationary salt wedge model. J. Geophys. Res 96, 12739–12754.Google Scholar
Stoker, J. J. 1957 Water Waves: The Mathematical Theory with Applications. Interscience.Google Scholar
Tickle, G. A. 1996 A model of the motion and dilution of a heavy gas cloud released on a uniform slope in calm conditions. J. Hazard. Mater. 49 (1), 29–47.Google Scholar
Toro, E. F. 2009 Riemann Solvers and Numerical Methods for Fluid Dynamics: A Practical Introduction. Springer.Google Scholar
Turner, J. S. 1973 Buoyancy Effects in Fluids. Cambridge University Press.Google Scholar
Turner, J. S. 1986 Turbulent entrainment: the development of the entrainment assumption, and its application to geophysical flows. J. Fluid Mech. 173, 431–471.Google Scholar
Ungarish, M. 2009 An Introduction to Gravity Currents and Intrusions. Chapman and Hall/CRC.Google Scholar