Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Blackbourn, Luke A. K.
and
Tran, Chuong V.
2011.
Effects of friction on forced two-dimensional Navier-Stokes turbulence.
Physical Review E,
Vol. 84,
Issue. 4,
San, Omer
and
Staples, Anne E.
2012.
High-order methods for decaying two-dimensional homogeneous isotropic turbulence.
Computers & Fluids,
Vol. 63,
Issue. ,
p.
105.
Ditlevsen, Peter D.
2012.
A stochastic model of cascades in two-dimensional turbulence.
Physics of Fluids,
Vol. 24,
Issue. 10,
Kitsios, Vassili
Frederiksen, Jorgen S.
and
Zidikheri, Meelis J.
2012.
Subgrid Model with Scaling Laws for Atmospheric Simulations.
Journal of the Atmospheric Sciences,
Vol. 69,
Issue. 4,
p.
1427.
Mininni, P. D.
and
Pouquet, A.
2013.
Inverse cascade behavior in freely decaying two-dimensional fluid turbulence.
Physical Review E,
Vol. 87,
Issue. 3,
Bowman, John C.
2013.
Casimir cascades in two-dimensional turbulence.
Journal of Fluid Mechanics,
Vol. 729,
Issue. ,
p.
364.
San, Omer
and
Staples, Anne E.
2013.
Stationary two-dimensional turbulence statistics using a Markovian forcing scheme.
Computers & Fluids,
Vol. 71,
Issue. ,
p.
1.
Deusebio, Enrico
Vallgren, A.
and
Lindborg, E.
2013.
The route to dissipation in strongly stratified and rotating flows.
Journal of Fluid Mechanics,
Vol. 720,
Issue. ,
p.
66.
Pouquet, A
Sen, A
Rosenberg, D
Mininni, P D
and
Baerenzung, J
2013.
Inverse cascades in turbulence and the case of rotating flows.
Physica Scripta,
Vol. T155,
Issue. ,
p.
014032.
Deusebio, E.
Boffetta, G.
Lindborg, E.
and
Musacchio, S.
2014.
Dimensional transition in rotating turbulence.
Physical Review E,
Vol. 90,
Issue. 2,
Matsumoto, Takeshi
and
Sakajo, Takashi
2016.
One-dimensional hydrodynamic model generating a turbulent cascade.
Physical Review E,
Vol. 93,
Issue. 5,
Maulik, R.
and
San, O.
2017.
A dynamic framework for functional parameterisations of the eddy viscosity coefficient in two-dimensional turbulence.
International Journal of Computational Fluid Dynamics,
Vol. 31,
Issue. 2,
p.
69.
Maulik, Romit
and
San, Omer
2017.
A stable and scale-aware dynamic modeling framework for subgrid-scale parameterizations of two-dimensional turbulence.
Computers & Fluids,
Vol. 158,
Issue. ,
p.
11.
Westernacher-Schneider, John Ryan
and
Lehner, Luis
2017.
Numerical measurements of scaling relations in two-dimensional conformal fluid turbulence.
Journal of High Energy Physics,
Vol. 2017,
Issue. 8,
Reeves, Matthew T.
Billam, Thomas P.
Yu, Xiaoquan
and
Bradley, Ashton S.
2017.
Enstrophy Cascade in Decaying Two-Dimensional Quantum Turbulence.
Physical Review Letters,
Vol. 119,
Issue. 18,
Eghdami, Masih
Bhushan, Shanti
and
Barros, Ana P.
2018.
Direct Numerical Simulations to Investigate Energy Transfer between Meso- and Synoptic Scales.
Journal of the Atmospheric Sciences,
Vol. 75,
Issue. 4,
p.
1163.
Sharma, Manohar K.
Verma, Mahendra K.
and
Chakraborty, Sagar
2018.
On the energy spectrum of rapidly rotating forced turbulence.
Physics of Fluids,
Vol. 30,
Issue. 11,
Matharu, Pritpal
and
Protas, Bartosz
2022.
Optimal eddy viscosity in closure models for two-dimensional turbulent flows.
Physical Review Fluids,
Vol. 7,
Issue. 4,
Ayapilla, Aditya Sai Pranith
2023.
A data-driven approach to model enstrophy transfers in large eddy simulation of forced two-dimensional turbulence.
Physics of Fluids,
Vol. 35,
Issue. 7,
Basu, Abhik
and
Bhattacharjee, Jayanta K.
2023.
Universal scaling regimes in rotating fluid turbulence.
Physical Review Fluids,
Vol. 8,
Issue. 6,
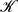 εω2/3k−3, without any logarithmic correction, where εω is the enstrophy dissipation and
εω2/3k−3, without any logarithmic correction, where εω is the enstrophy dissipation and 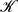 is of the order of unity. However,
is of the order of unity. However, 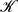 is varying between different simulations and is thus not a perfect constant. This variation can be understood as a consequence of large-scale dissipation intermittency, following the argument by Landau (Landau & Lifshitz, Fluid Mechanics, 1959, Pergamon). In the presence of a large-scale drag, we obtain a slightly steeper spectrum. When forcing is applied at a scale which is somewhat smaller than the computational domain, no vortices are formed, and the statistics remain close to Gaussian in the enstrophy cascade range. When forcing is applied at a smaller scale, long-lived coherent vortices form at larger scales than the forcing scale, and intermittency measures become very large at all scales, including the scales of the enstrophy cascade. We conclude that the enstrophy cascade with a k−3-spectrum is a robust feature of the two-dimensional Navier–Stokes equations. However, there is a complete lack of universality of higher-order statistics of vorticity increments in the enstrophy cascade range.
is varying between different simulations and is thus not a perfect constant. This variation can be understood as a consequence of large-scale dissipation intermittency, following the argument by Landau (Landau & Lifshitz, Fluid Mechanics, 1959, Pergamon). In the presence of a large-scale drag, we obtain a slightly steeper spectrum. When forcing is applied at a scale which is somewhat smaller than the computational domain, no vortices are formed, and the statistics remain close to Gaussian in the enstrophy cascade range. When forcing is applied at a smaller scale, long-lived coherent vortices form at larger scales than the forcing scale, and intermittency measures become very large at all scales, including the scales of the enstrophy cascade. We conclude that the enstrophy cascade with a k−3-spectrum is a robust feature of the two-dimensional Navier–Stokes equations. However, there is a complete lack of universality of higher-order statistics of vorticity increments in the enstrophy cascade range.