Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Wang, Hongping
Yang, Zixuan
Wu, Ting
and
Wang, Shizhao
2021.
Coherent structures associated with interscale energy transfer in turbulent channel flows.
Physical Review Fluids,
Vol. 6,
Issue. 10,
Tang, Zhanqi
Chen, Letian
Fan, Ziye
Ma, Xingyu
and
Jiang, Nan
2021.
Cross-term events of scale-decomposed skewness factor in turbulent boundary layer at moderate Reynolds number.
Physics of Fluids,
Vol. 33,
Issue. 5,
Wang, Chengyue
Gao, Qi
Wang, Biao
Pan, Chong
and
Wang, Jinjun
2021.
Vortex-to-velocity reconstruction for wall-bounded turbulence via the field-based linear stochastic estimation.
Journal of Fluid Mechanics,
Vol. 922,
Issue. ,
Yu, Jiaming
Zhu, Yiding
Gu, Dingwei
and
Lee, Cunbiao
2022.
A thermoacoustic heat pump driven by acoustic waves in a hypersonic boundary layer.
Physics of Fluids,
Vol. 34,
Issue. 1,
Kawata, T.
and
Tsukahara, T.
2022.
Spectral analysis on dissimilarity between turbulent momentum and heat transfers in plane Couette turbulence.
Physics of Fluids,
Vol. 34,
Issue. 7,
Dong, Siwei
Tong, Fulin
Yu, Ming
Chen, Jianqiang
Yuan, Xianxu
and
Wang, Qian
2022.
Positive and negative pairs of fluctuating wall shear stress and heat flux in supersonic turbulent boundary layers.
Physics of Fluids,
Vol. 34,
Issue. 8,
Long, Yanguang
Wang, Jinjun
and
Pan, Chong
2022.
Universal modulations of large-scale motions on entrainment of turbulent boundary layers.
Journal of Fluid Mechanics,
Vol. 941,
Issue. ,
Wang, Wenkang
Lozano-Durán, Adrián
Helmig, Rainer
and
Chu, Xu
2022.
Spatial and spectral characteristics of information flux between turbulent boundary layers and porous media.
Journal of Fluid Mechanics,
Vol. 949,
Issue. ,
Kawata, Takuya
and
Tsukahara, Takahiro
2022.
Spectral Analysis on Transport Budgets of Turbulent Heat Fluxes in Plane Couette Turbulence.
Energies,
Vol. 15,
Issue. 14,
p.
5258.
De Leo, A.
and
Stocchino, A.
2023.
Efficiency of energy and enstrophy transfers in periodical flows.
Physics of Fluids,
Vol. 35,
Issue. 4,
Wu, Huijie
and
Wang, Binbin
2023.
Spectral turbulence kinetic energy budget and scale-based velocity decomposition for turbulence in bubble plumes.
Physics of Fluids,
Vol. 35,
Issue. 6,
2023.
Reduced-order representation of superstructures in a turbulent boundary layer.
Physics of Fluids,
Vol. 35,
Issue. 5,
Parthasarathy, Aadhy S.
and
Saxton-Fox, Theresa
2023.
Spectral analysis of a turbulent boundary layer encountering steady and unsteady complex pressure gradients.
Xuesen, Chu
Yaoyao, Liu
Zhenxun, Dong
Chong, Pan
Yuehong, Qian
Kai, Yan
and
Guangwen, Yang
2023.
Direct simulation of flow field around SUBOFF in grid-generated turbulence with SWLBM.
Computers & Fluids,
Vol. 265,
Issue. ,
p.
106019.
Cimarelli, A.
Boga, G.
Pavan, A.
Costa, P.
and
Stalio, E.
2024.
Spatially evolving cascades in wall turbulence with and without interface.
Journal of Fluid Mechanics,
Vol. 987,
Issue. ,
Ling, Weihao
Gao, Song
Wang, Zhiheng
Zeng, Min
Huang, Wenlin
and
Xi, Guang
2024.
Direct numerical simulation of boundary layer transition induced by roughness element in a low Reynolds number compressor blade.
Physics of Fluids,
Vol. 36,
Issue. 12,
Cimarelli, Andrea
Boga, Gabriele
Pavan, Anna
Costa, Pedro
and
Stalio, Enrico
2024.
Energy Cascade Phenomena in Temporal Boundary Layers.
Flow, Turbulence and Combustion,
Vol. 112,
Issue. 1,
p.
129.
Li, X. X.
Hu, R. F.
and
Fang, L.
2024.
Scaling laws of velocity gradient moments of attached eddies.
Physical Review Fluids,
Vol. 9,
Issue. 9,
Zhang, Yi
Pan, Chong
Wang, Jinjun
and
Zhang, Miao
2024.
Modulating multi-scale motions in a turbulent boundary layer by micro vortex generators.
Physics of Fluids,
Vol. 36,
Issue. 8,
Dong, Zhen-xun
Pan, Chong
Tong, Fu-lin
and
Yuan, Xian-xu
2024.
Variation of vortical structures across shock-wave/turbulent boundary-layer interaction region in a compression ramp flow.
Physics of Fluids,
Vol. 36,
Issue. 5,
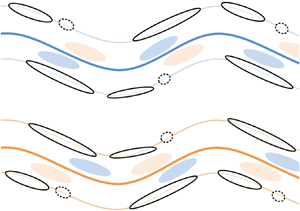
 $Re_{\tau }=1200\text {--}3500$), which are obtained via a two-dimensional (2-D) particle image velocimetry measurement with large field-of-view. Two types of energy flux, i.e. local interscale energy flux and in-plane spatial energy flux are inspected in detail. Targeting the energy transfer in large-scale regime, an anisotropic filter is designed based on the zero-crossing scale boundary in a 2-D energy transfer spectrum, across which the net energy flux is the maximum. This ‘optimal’ energy flux boundary separates the scale space into an energy donating large-scale part and an energy receiving small-scale one. The crossover energy flux, as well as the associated flow field structures, are studied by conditional statistics and linear stochastic estimation, in which the statistical spanwise symmetry is deliberately broken by designing special velocity gradient conditions for event probing. A strong connection between large-scale energy flux events and LSMs are found. Namely, forward scatter events have higher probability to reside on the wavy flank of low-momentum LSMs, if compared with the scenario of being clamped in the middle of two streamwise-aligned high- and low-momentum LSMs (Natrajan & Christensen, Phys. Fluids, vol. 18, issue 6, 2006, pp. 299–325). Meanwhile, pairs of positive and negative spatial transfer events tend to locate inside LSMs. It is thus argued that the meandering nature of LSMs, which forms the necessary velocity gradient, might play a determining role in the process of large-scale energy transfer. The spatial correlation between them is then schematized in a conceptual model, which explains most of the present observations.
$Re_{\tau }=1200\text {--}3500$), which are obtained via a two-dimensional (2-D) particle image velocimetry measurement with large field-of-view. Two types of energy flux, i.e. local interscale energy flux and in-plane spatial energy flux are inspected in detail. Targeting the energy transfer in large-scale regime, an anisotropic filter is designed based on the zero-crossing scale boundary in a 2-D energy transfer spectrum, across which the net energy flux is the maximum. This ‘optimal’ energy flux boundary separates the scale space into an energy donating large-scale part and an energy receiving small-scale one. The crossover energy flux, as well as the associated flow field structures, are studied by conditional statistics and linear stochastic estimation, in which the statistical spanwise symmetry is deliberately broken by designing special velocity gradient conditions for event probing. A strong connection between large-scale energy flux events and LSMs are found. Namely, forward scatter events have higher probability to reside on the wavy flank of low-momentum LSMs, if compared with the scenario of being clamped in the middle of two streamwise-aligned high- and low-momentum LSMs (Natrajan & Christensen, Phys. Fluids, vol. 18, issue 6, 2006, pp. 299–325). Meanwhile, pairs of positive and negative spatial transfer events tend to locate inside LSMs. It is thus argued that the meandering nature of LSMs, which forms the necessary velocity gradient, might play a determining role in the process of large-scale energy transfer. The spatial correlation between them is then schematized in a conceptual model, which explains most of the present observations.