Hostname: page-component-745bb68f8f-g4j75 Total loading time: 0 Render date: 2025-01-09T22:08:13.319Z Has data issue: false hasContentIssue false
  • English
  • Français

Energy spectra of stably stratified turbulence

Published online by Cambridge University Press:  27 March 2012

Y. Kimura  and
J. R. Herring
Y. Kimura*
Affiliation:
Graduate School of Mathematics, Nagoya University, Furo-cho, Chikusa-ku, Nagoya 464-8602, Japan
J. R. Herring
Affiliation:
National Center for Atmospheric Research, P.O. Box 3000, Boulder, CO 80307-3000, USA
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

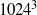We investigate homogeneous incompressible turbulence subjected to a range of degrees of stratification. Our basic method is pseudospectral direct numerical simulations at a resolution of . Such resolution is sufficient to reveal inertial power-law ranges for suitably comprised horizontal and vertical spectra, which are designated as the wave and vortex mode (the Craya–Herring representation). We study mainly turbulence that is produced from randomly large-scale forcing via an Ornstein–Uhlenbeck process applied isotropically to the horizontal velocity field. In general, both the wave and vortex spectra are consistent with a Kolmogorov-like range at sufficiently large 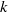. At large scales, and for sufficiently strong stratification, the wave spectrum is a steeper 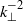, while that for the vortex component is consistent with 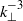. Here 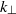is the horizontally gathered wavenumber. In contrast to the horizontal wavenumber spectra, the vertical wavenumber spectra show very different features. For those spectra, a clear 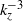dependence for small scales is observed while the large scales show rather flat spectra. By modelling the horizontal layering of vorticity, we attempt to explain the flat spectra. These spectra are linked to two-point structure functions of the velocity correlations in the horizontal and vertical directions. We can observe the power-law transition also in certain of the two-point structure functions.

JFM classification

Turbulent Flows: Homogeneous turbulence Geophysical and Geological Flows: Stratified flows Turbulent Flows: Turbulence simulation
Type
Papers
Information
Journal of Fluid Mechanics , Volume 698 , 10 May 2012 , pp. 19 - 50
Copyright
Copyright © Cambridge University Press 2012

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1. Billant, P. & Chomaz, J.-M. 2000 Experimental evidence for a new instability of a vertical columnar vortex pair in a strongly stratified fluid. J. Fluid Mech. 418, 167–188.CrossRefGoogle Scholar
2. Brethouwer, G., Billant, P., Lindborg, E. & Chomaz, J.-M. 2007 Scaling analysis and simulation of strongly stratified turbulent flows. J. Fluid Mech. 585, 343–368.CrossRefGoogle Scholar
3. Cambon, C., Jacquin, D. & Mathieu, J. 1981 Spectral modeling of homogeneous non-isotropic turbulence. J. Fluid Mech. 104, 247–262.CrossRefGoogle Scholar
4. Carnevale, G. F., Briscolini, M. & Orlandi, P. 2001 Buoyancy- to inertial-range transition in forced stratified turbulence. J. Fluid Mech. 427, 205–239.CrossRefGoogle Scholar
5. Cho, J. Y. N. & Lindborg, E. 2001 Horizontal velocity structure functions in the upper troposphere and lower stratosphere 1. Observation. J. Geophys. Res. 106, 10 223–10 232.CrossRefGoogle Scholar
6. Craya, A. 1958Contribution à l’analyse de la turbulence associée à des vitesse moyennes. Publ. Sci. Tech. Ministère de l’Air (France), no. 345.Google Scholar
7. Dewan, E. M. 1979 Stratospheric wave spectra resembling turbulence. Science 204, 832–835.Google Scholar
8. Dewan, E. M. & Good, R. E. 1986 Saturation and the ‘universal’ spectrum for vertical profiles of horizontal scalar winds in the atmosphere. J. Geophys. Res. 91, 2742–2748.CrossRefGoogle Scholar
9. Dillon, T. M. & Caldwell, D. R. 1980 The Batchelor spectrum and dissipation in the upper ocean. J. Geophys. Res. 85, 1910–1916.CrossRefGoogle Scholar
10. Eswaran, V. & Pope, S. B. 1988 An examination of forcing in direct numerical simulations of turbulence. Comput. Fluids 16, 257–278.CrossRefGoogle Scholar
11. Gage, K. S. 1979 Evidence for a law inertial range in mesoscale two-dimensional turbulence. J. Atmos. Sci. 36, 1950–1954.Google Scholar
12. Galperin, B. & Sukoriansky, S. 2010 Geophysical flows with anisotropic turbulence and dispersive waves with stable stratification. Ocean Dyn. 144, 1319–1327.CrossRefGoogle Scholar
13. Gargett, A. E., Hendricks, P. J., Sanford, T. B., Osborn, T. R. & Williams, A. J. 1981 A composite spectrum of vertical shear in the upper ocean. J. Phys. Oceanogr. 11, 1258–1271.2.0.CO;2>CrossRefGoogle Scholar
14. Gargett, A. E., Osborn, T. R. & Nasmyth, P. W. 1984 Local isotropy and the decay of turbulence in a stratified fluid. J. Fluid Mech. 144, 231–280.Google Scholar
15. Godeferd, F. S. & Cambon, C. 1994 Detailed investigation of energy transfers in homogeneous stratified turbulence. Phys. Fluids 6, 2084–2100.CrossRefGoogle Scholar
16. Godeferd, S. & Staquet, C. 2003 Statistical modeling and direct numerical simulations of decaying stratified turbulence. Part 2. Large scale and small scale anisotropy. J. Fluid Mech. 486, 115–159.CrossRefGoogle Scholar
17. Gregg, M. C. 1987 Diapycnal mixing in the thermocline: a review. J. Geophys. Res. 92, 5249–5286.Google Scholar
18. Herring, J. R. & Métais, O. 1989 Numerical experiments in forced stably stratified turbulence. J. Fluid Mech. 202, 97–115.CrossRefGoogle Scholar
19. Holloway, G. 1988 The buoyancy flux from internal gravity wave breaking. Dyn. Atmos. Oceans 12, 107–125.CrossRefGoogle Scholar
20. Kimura, Y. & Herring, J. R. 1996 Diffusion in stably stratified turbulence. J. Fluid Mech. 328, 253–269.Google Scholar
21. Kitamura, Y. & Matsuda, Y. 2006 The and energy spectra in stratified turbulence. Geophys. Res. Lett. 33, L05809.Google Scholar
22. Kurien, S., Wingate, B. & Taylor, M. A. 2008 Anisotropic constraints on energy distribution in rotating and stratified turbulence. Europhys. Lett. 84, 24003.CrossRefGoogle Scholar
23. Lilly, D. K. 1983 Stratified turbulence and the mesoscale variability of the atmosphere. J. Atmos. Sci. 40, 749–761.Google Scholar
24. Lindborg, E. 2006 The energy cascade in a strongly stratified fluid. J. Fluid Mech. 550, 207–242.Google Scholar
25. Lindborg, E. & Cho, J. Y. N. 2001 Horizontal velocity structure functions in the upper troposphere and lower stratosphere 2. Theoretical considerations. J. Geophys. Res. 106, 10 233–10 241.Google Scholar
26. Nastrom, G. D. & Gage, K. S. 1985 A climatology of atmospheric wavenumber spectra of wind and temperature observed by commercial aircraft. J. Atmos. Sci. 42, 950–960.Google Scholar
27. Riley, J. J. & de Bruyn Kops, S. M. 2003 Dynamics of turbulence strongly influenced by buoyancy. Phys. Fluids 15, 2047–2059.CrossRefGoogle Scholar
28. Riley, J. J. & Lindborg, E. 2008 Stratified turbulence: a possible interpretation of some geophysical turbulence measurements. J. Atmos. Sci. 65, 2416–2424.Google Scholar
29. Saffman, P. G. 1971 On the spectrum and decay of random two-dimensional vorticity distributions of large Reynolds number. Stud. Appl. Maths 50, 377–383.CrossRefGoogle Scholar
30. Sagaut, P. & Cambon, C. 2008 Homogeneous Turbulence Dynamics. Cambridge University Press.Google Scholar
31. Smith, S. A., Fritts, D. C. & Van Zandt, T. E. 1987 Evidence for a saturated spectrum of atmospheric gravity waves. J. Atmos. Sci. 44, 1404–1410.2.0.CO;2>CrossRefGoogle Scholar
32. Spalart, P. R., Moser, R. D. & Rogers, M. M. 1991 Spectral methods for the Navier–Stokes equations with one infinite and two periodic directions. J. Comput. Phys. 96, 297.CrossRefGoogle Scholar
33. Sreenivasan, K. R. 1995 On the universality of the Kolmogorov constant. Phys. Fluids 7, 2778–2784.Google Scholar
34. Staquet, C. 2000 Mixing in a stably stratified shear layer: two- and three-dimensional numerical experiments. Fluid Dyn. Res. 27, 367–404.Google Scholar
35. Staquet, C. & Sommeria, J. 2002 Internal gravity waves: from instabilities to turbulence. Annu. Rev. Fluid Mech. 34, 559–593.CrossRefGoogle Scholar
36. Sullivan, P. P. & Patton, E. G. 2011 The effect of mesh resolution on convective boundary layer statistics and structures generated by large-eddy simulation. J. Atmos. Sci. 68, 2395–2415.Google Scholar
37. Turner, J. S. 1973 Buoyancy Effects in Fluids. Cambridge University Press.Google Scholar
38. Van Zandt, T. E. 1982 A universal spectrum of buoyancy waves in the atmosphere. Geophys. Res. Lett. 9, 575–578.CrossRefGoogle Scholar
39. Waite, M. L. & Bartello, P. 2004 Stratified turbulence dominated by vortical motion. J. Fluid Mech. 517, 281–308.CrossRefGoogle Scholar
40. Waite, M. L. & Bartello, P. 2006 Stratified turbulence generated by internal gravity waves. J. Fluid Mech. 546, 313–339.Google Scholar
41. Yeung, P. K. & Pope, S. B. 1989 Lagrangian statistics from direct numerical simulations of isotropic turbulence. J. Fluid Mech. 207, 531–586.CrossRefGoogle Scholar