Hostname: page-component-586b7cd67f-2brh9 Total loading time: 0 Render date: 2024-11-23T14:43:26.817Z Has data issue: false hasContentIssue false
  • English
  • Français

Energy flux enhancement, intermittency and turbulence via Fourier triad phase dynamics in the 1-D Burgers equation

Published online by Cambridge University Press:  06 July 2018

Brendan P. Murray  and
Miguel D. Bustamante Open the ORCID record for Miguel D. Bustamante [Opens in a new window]
Brendan P. Murray
Affiliation:
Institute for Discovery, Department of Mathematics and Statistics, University College Dublin, Belfield D4, Ireland
Miguel D. Bustamante*
Affiliation:
Institute for Discovery, Department of Mathematics and Statistics, University College Dublin, Belfield D4, Ireland
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We present a theoretical and numerical study of Fourier-space triad phase dynamics in the one-dimensional stochastically forced Burgers equation at Reynolds number 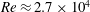$Re\approx 2.7\times 10^{4}$. We demonstrate that Fourier triad phases over the inertial range display a collective behaviour characterised by intermittent periods of synchronisation and alignment, reminiscent of the Kuramoto model (Chemical Oscillations, Waves, and Turbulence, Springer, 1984) and directly related to collisions of shocks in physical space. These periods of synchronisation favour efficient energy fluxes across the inertial range towards small scales, resulting in strong bursts of dissipation and enhanced coherence of the Fourier energy spectrum. The fast time scale of the onset of synchronisation relegates energy dynamics to a passive role: this is further examined using a reduced system with the Fourier amplitudes fixed in time – a phase-only model. We show that intermittent triad phase dynamics persists without amplitude evolution and we broadly recover many of the characteristics of the full Burgers system. In addition, for both full Burgers and phase-only systems the physical-space velocity statistics reveals that triad phase alignment is directly related to the non-Gaussian statistics typically associated with structure-function intermittency in turbulent systems.

JFM classification

Turbulent Flows: Intermittency Compressible Flows: Shock waves Turbulent Flows: Turbulence theory
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 850 , 10 September 2018 , pp. 624 - 645
Check for updates
Copyright
© 2018 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Arguedas-Leiva, J.-A.2017 Phase coherence and intermittency of a turbulent field based on a system of coupled oscillators. Master Thesis, Institut für Nichtlineare Dynamik, Georg-August-Universität Göttingen, 2017.Google Scholar
Bec, J. & Khanin, K. 2007 Burgers turbulence. Phys. Rep. 447 (1), 1–66.Google Scholar
Bessis, D. & Fournier, J. D. 1984 Pole condensation and the Riemann surface associated with a shock in Burgers’ equation. J. Phys. Lett. 45 (17), 833–841.Google Scholar
Bessis, D. & Fournier, J. D. 1990 Complex singularities and the Riemann surface for the Burgers equation. In Nonlinear Physics, pp. 252–257. Springer.Google Scholar
Bustamante, M. D. & Kartashova, E. 2009 Effect of the dynamical phases on the nonlinear amplitudes’ evolution. Europhys. Lett. 85 (3), 34002.Google Scholar
Bustamante, M. D., Quinn, B. & Lucas, D. 2014 Robust energy transfer mechanism via precession resonance in nonlinear turbulent wave systems. Phys. Rev. Lett. 113 (8), 084502.Google Scholar
Buzzicotti, M., Biferale, L., Frisch, U. & Ray, S. S. 2016a Intermittency in fractal Fourier hydrodynamics: lessons from the Burgers equation. Phys. Rev. E 93 (3), 033109.Google Scholar
Buzzicotti, M., Murray, B. P., Biferale, L. & Bustamante, M. D. 2016b Phase and precession evolution in the Burgers equation. Eur. Phys. J. E 39 (3), 34.Google Scholar
Caflisch, R., Gargano, F., Sammartino, M. & Sciacca, V. 2015 Complex singularities and PDEs. Rivista di Matematica della Università di Parma 6 (1), 69–133.Google Scholar
Calogero, F. 1978 Motion of poles and zeros of special solutions of nonlinear and linear partial differential equations and related «solvable» many-body problems. Il Nuovo Cimento B (1971–1996) 43 (2), 177–241.Google Scholar
Chian, A. C.-L., Miranda, R. A., Rempel, E. L., Saiki, Y. & Yamada, M. 2010 Amplitude-phase synchronization at the onset of permanent spatiotemporal chaos. Phys. Rev. Lett. 104 (25), 254102.Google Scholar
Chiang, L.-Y. & Coles, P. 2000 Phase information and the evolution of cosmological density perturbations. Mon. Not. R. Astron. Soc. 311 (4), 809–824.Google Scholar
Choodnovsky, D. V. & Choodnovsky, G. V. 1977 Pole expansions of nonlinear partial differential equations. Il Nuovo Cimento B 40 (2), 339–353.Google Scholar
Cichowlas, C. & Brachet, M.-E. 2005 Evolution of complex singularities in Kida–Pelz and Taylor–Green inviscid flows. Fluid Dyn. Res. 36 (4–6), 239–248.Google Scholar
Craik, A. D. D. 1988 Wave Interactions and Fluid Flows. Cambridge University Press.Google Scholar
Frisch, U. 1995 Turbulence: The Legacy of A. N. Kolmogorov. Cambridge University Press.Google Scholar
Frisch, U., Pomyalov, A., Procaccia, I. & Ray, S. S. 2012 Turbulence in noninteger dimensions by fractal Fourier decimation. Phys. Rev. Lett. 108 (7), 074501.Google Scholar
Harris, J., Bustamante, M. D. & Connaughton, C. 2012 Externally forced triads of resonantly interacting waves: boundedness and integrability properties. Commun. Nonlinear Sci. Numer. Simul. 17 (12), 4988–5006.Google Scholar
Kida, S. 1986 Study of complex singularities by filtered spectral method. J. Phys. Soc. Japan 55 (5), 1542–1555.Google Scholar
Kim, W. & West, B. J. 1997 Chaotic properties of internal wave triad interactions. Phys. Fluids 9 (3), 632–647.Google Scholar
Kraichnan, R. H. 1967 Inertial ranges in two-dimensional turbulence. Phys. Fluids 10 (7), 1417–1423.Google Scholar
Kuramoto, Y. 1984 Chemical Oscillations, Waves, and Turbulence. Springer.Google Scholar
Miranda, R. A., Rempel, E. L. & Chian, A. C.-L. 2015 On–off intermittency and amplitude-phase synchronization in Keplerian shear flows. Mon. Not. R. Astron. Soc. 448 (1), 804–813.Google Scholar
Morf, R. H., Orszag, S. A., Meiron, D. I., Meneguzzi, M. & Frisch, U. 1981 Analytic structure of high Reynolds number flows. In Seventh International Conference on Numerical Methods in Fluid Dynamics, pp. 292–298. Springer.Google Scholar
Nazarenko, S. 2011 Wave Turbulence. Springer Science & Business Media.Google Scholar
Senouf, D. 1997 Dynamics and condensation of complex singularities for Burgers’ equation i. SIAM J. Math. Anal. 28 (6), 1457–1489.Google Scholar
Senouf, D., Caflisch, R. & Ercolani, N. 1996 Pole dynamics and oscillations for the complex Burgers equation in the small-dispersion limit. Nonlinearity 9 (6), 1671.Google Scholar
Strogatz, S. H. 2000 From Kuramoto to Crawford: exploring the onset of synchronization in populations of coupled oscillators. Physica D 143, 1–20.Google Scholar
Sulem, C., Sulem, P.-L. & Frisch, H. 1983 Tracing complex singularities with spectral methods. J. Comput. Phys. 50 (1), 138–161.Google Scholar
Thompson, J. R. & Roy, R. 1991 Nonlinear dynamics of multiple four-wave mixing processes in a single-mode fiber. Phys. Rev. A 43 (9), 4987–4996.Google Scholar
Trillo, S., Wabnitz, S. & Kennedy, T. A. B. 1994 Nonlinear dynamics of dual-frequency-pumped multiwave mixing in optical fibers. Phys. Rev. A 50 (2), 1732–1747.Google Scholar
Weideman, J. A. C. 2003 Computing the dynamics of complex singularities of nonlinear PDEs. SIAM J. Appl. Dynam. Syst. 2 (2), 171–186.Google Scholar
Wilczek, M., Vlaykov, D. G. & Lalescu, C. C. 2017 Emergence of non-Gaussianity in turbulence. In Progress in Turbulence VII, pp. 3–9. Springer.Google Scholar
Supplementary material: File

Murray and Bustamante supplementary material

Murray and Bustamante supplementary material 1

Download Murray and Bustamante supplementary material(File)
File 1.5 MB