Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Hughes, Graham O.
Gayen, Bishakhdatta
and
Griffiths, Ross W.
2013.
Available potential energy in Rayleigh–Bénard convection.
Journal of Fluid Mechanics,
Vol. 729,
Issue. ,
Griffiths, Ross W.
Hughes, Graham O.
and
Gayen, Bishakhdatta
2013.
Horizontal convection dynamics: insights from transient adjustment.
Journal of Fluid Mechanics,
Vol. 726,
Issue. ,
p.
559.
Gayen, Bishakhdatta
Hughes, Graham O.
and
Griffiths, Ross W.
2013.
Completing the Mechanical Energy Pathways in Turbulent Rayleigh-Bénard Convection.
Physical Review Letters,
Vol. 111,
Issue. 12,
Cessi, Paola
Pinardi, Nadia
and
Lyubartsev, Vladislav
2014.
Energetics of Semienclosed Basins with Two-Layer Flows at the Strait.
Journal of Physical Oceanography,
Vol. 44,
Issue. 3,
p.
967.
Hussam, Wisam K.
Tsai, Tze K.
and
Sheard, Gregory J.
2014.
The effect of rotation on radial horizontal convection and Nusselt number scaling in a cylindrical container.
International Journal of Heat and Mass Transfer,
Vol. 77,
Issue. ,
p.
46.
Ilıcak, Mehmet
2014.
Energetics and mixing efficiency of lock-exchange flow.
Ocean Modelling,
Vol. 83,
Issue. ,
p.
1.
Gayen, Bishakhdatta
Griffiths, Ross W.
and
Hughes, Graham O.
2014.
Stability transitions and turbulence in horizontal convection.
Journal of Fluid Mechanics,
Vol. 751,
Issue. ,
p.
698.
Davies Wykes, Megan S.
Hughes, Graham O.
and
Dalziel, Stuart B.
2015.
On the meaning of mixing efficiency for buoyancy-driven mixing in stratified turbulent flows.
Journal of Fluid Mechanics,
Vol. 781,
Issue. ,
p.
261.
Griffiths, Ross W.
and
Gayen, Bishakhdatta
2015.
Turbulent Convection Insights from Small-Scale Thermal Forcing with Zero Net Heat Flux at a Horizontal Boundary.
Physical Review Letters,
Vol. 115,
Issue. 20,
Paparella, Francesco
2016.
Mathematical Paradigms of Climate Science.
Vol. 15,
Issue. ,
p.
15.
Tsai, Tzekih
Hussam, Wisam K.
Fouras, Andreas
and
Sheard, Gregory J.
2016.
The origin of instability in enclosed horizontally driven convection.
International Journal of Heat and Mass Transfer,
Vol. 94,
Issue. ,
p.
509.
Vreugdenhil, Catherine A.
Gayen, Bishakhdatta
and
Griffiths, Ross W.
2016.
Mixing and dissipation in a geostrophic buoyancy‐driven circulation.
Journal of Geophysical Research: Oceans,
Vol. 121,
Issue. 8,
p.
6076.
Vreugdenhil, Catherine A.
Hogg, Andrew McC.
Griffiths, Ross W.
and
Hughes, Graham O.
2016.
Adjustment of the Meridional Overturning Circulation and Its Dependence on Depth of Mixing.
Journal of Physical Oceanography,
Vol. 46,
Issue. 3,
p.
731.
Gayen, Bishakhdatta
Griffiths, Ross W.
and
Kerr, Ross C.
2016.
Simulation of convection at a vertical ice face dissolving into saline water.
Journal of Fluid Mechanics,
Vol. 798,
Issue. ,
p.
284.
Sanmiguel Vila, Carlos
Discetti, Stefano
Carlomagno, Giovanni Maria
Astarita, Tommaso
and
Ianiro, Andrea
2016.
On the onset of horizontal convection.
International Journal of Thermal Sciences,
Vol. 110,
Issue. ,
p.
96.
Shishkina, Olga
and
Wagner, Sebastian
2016.
Prandtl-Number Dependence of Heat Transport in Laminar Horizontal Convection.
Physical Review Letters,
Vol. 116,
Issue. 2,
Shishkina, Olga
Grossmann, Siegfried
and
Lohse, Detlef
2016.
Heat and momentum transport scalings in horizontal convection.
Geophysical Research Letters,
Vol. 43,
Issue. 3,
p.
1219.
Leigh, Matthew A.
Tsai, Tzekih
and
Sheard, Gregory J.
2016.
Probing horizontal convection instability via perturbation of the forcing boundary layer using a synthetic jet.
International Journal of Thermal Sciences,
Vol. 110,
Issue. ,
p.
251.
Stewart, K.D.
Hogg, A.McC.
Griffies, S.M.
Heerdegen, A.P.
Ward, M.L.
Spence, P.
and
England, M.H.
2017.
Vertical resolution of baroclinic modes in global ocean models.
Ocean Modelling,
Vol. 113,
Issue. ,
p.
50.
Rosevear, Madelaine G.
Gayen, Bishakhdatta
and
Griffiths, Ross W.
2017.
Turbulent horizontal convection under spatially periodic forcing: a regime governed by interior inertia.
Journal of Fluid Mechanics,
Vol. 831,
Issue. ,
p.
491.
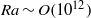 $\mathit{Ra}\sim O(1{0}^{12} )$, and boundary conditions that allow comparison with previous laboratory experiments. The convection is forced by heating over half of the horizontal base of a long channel and cooling over the other half of the base. The solutions are consistent with the experiments, including small-scale streamwise roll instability developing into a convectively mixed layer within the bottom thermal boundary layer, and a turbulent endwall plume. The mechanical energy budget is shown to be dominated by conversions of available potential energy to kinetic energy by buoyancy flux in the plume and the reverse in the interior of the circulation. These local conversions are three orders of magnitude greater than the total rate of viscous dissipation. The total irreversible mixing is exactly equal to the generation of available potential energy by buoyancy forcing, and one order of magnitude larger than the viscous dissipation. This confirms that dissipation rate is not an indicator of the strength of the circulation and explains why horizontal convection is more energetic than might be expected.
$\mathit{Ra}\sim O(1{0}^{12} )$, and boundary conditions that allow comparison with previous laboratory experiments. The convection is forced by heating over half of the horizontal base of a long channel and cooling over the other half of the base. The solutions are consistent with the experiments, including small-scale streamwise roll instability developing into a convectively mixed layer within the bottom thermal boundary layer, and a turbulent endwall plume. The mechanical energy budget is shown to be dominated by conversions of available potential energy to kinetic energy by buoyancy flux in the plume and the reverse in the interior of the circulation. These local conversions are three orders of magnitude greater than the total rate of viscous dissipation. The total irreversible mixing is exactly equal to the generation of available potential energy by buoyancy forcing, and one order of magnitude larger than the viscous dissipation. This confirms that dissipation rate is not an indicator of the strength of the circulation and explains why horizontal convection is more energetic than might be expected.