Hostname: page-component-586b7cd67f-t7czq Total loading time: 0 Render date: 2024-11-23T18:00:52.377Z Has data issue: false hasContentIssue false
  • English
  • Français

Emulsion flow through a packed bed with multiple drop breakup

Published online by Cambridge University Press:  22 May 2013

Alexander Z. Zinchenko  and
Robert H. Davis
Alexander Z. Zinchenko*
Affiliation:
Department of Chemical and Biological Engineering, University of Colorado, Boulder, CO 80309-0424, USA
Robert H. Davis
Affiliation:
Department of Chemical and Biological Engineering, University of Colorado, Boulder, CO 80309-0424, USA
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Pressure-driven squeezing of a concentrated emulsion of deformable drops through a randomly packed granular material is studied by rigorous three-dimensional multidrop–multiparticle simulations at low Reynolds numbers. The drops are comparable in size with granular particles, so the drop phase and the carrier fluid have different permeabilities, and the emulsion cannot be treated as single phase. Squeezing requires significant drop deformation and can meet much resistance, depending on the capillary number 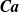$\boldsymbol{Ca}$. The granular material is modelled as a random loose packing (RLP) of many highly-frictional rigid monodisperse spheres in a periodic cell in mechanical equilibrium. Flow simulations for many drops squeezing through the network of solid spheres are performed by an extension of the multipole-accelerated boundary-integral (BI) algorithm of Zinchenko & Davis (J. Comput. Phys., vol. 227, 2008, pp. 7841–7888). A major improvement is robust mesh control on drop surfaces combined with a novel fragmentation algorithm, now allowing for long-time simulations with intricate drop shapes and multiple breakups. A major challenge is that up to 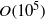$O(1{0}^{5} )$ time steps are required in a simulation for time averaging, and 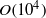$O(1{0}^{4} )$ boundary elements per surface to sufficiently resolve lubrication and breakups. Such simulations are feasible due to multipole acceleration, with two orders-of-magnitude gain over the standard BI coding. For initial drop-to-particle size ratio 0.51–0.52, emulsion concentration 41–42 % in the available space, and matching viscosities, time- and ensemble-averaged permeabilities of the drop phase and the continuous phase are studied versus 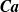$\boldsymbol{Ca}$ for systems of different size (up to 36 particles and 100 drops in a periodic cell). An avalanche of drop breakups observed at sufficiently large 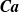$\boldsymbol{Ca}$ does not preclude the permeabilities from reaching a statistical steady state in a feasible simulation time. The critical, system-size-independent 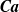$\boldsymbol{Ca}$, when the drop-phase flow effectively stops due to blockage in the pores by capillary forces, is estimated from simulations. For a sample RLP configuration, deep distinctions are found between the flow of concentrated emulsions and single-drop motion.

JFM classification

Drops and Bubbles: Drops and Bubbles Complex Fluids: Emulsions Low-Reynolds-number flows: Porous media
Type
Papers
Information
Journal of Fluid Mechanics , Volume 725 , 25 June 2013 , pp. 611 - 663
Copyright
©2013 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Bazhlekov, I. B., Anderson, P. D. & Meijer, H. E. H. 2004 Nonsingular boundary integral method for deformable drops in viscous flows. Phys. Fluids 16, 1064–1081.Google Scholar
Chhabra, R. P. & Srinivas, B. K. 1991 Non-Newtonian (purely viscous) fluid flow through packed beds: effect of particle shape. Powder Tech. 67, 15–19.CrossRefGoogle Scholar
Chapman, A. M. & Higdon, J. J. L. 1992 Oscillatory Stokes flow in periodic porous media. Phys. Fluids A 4, 2099–2116.Google Scholar
Cobos, S., Carvalho, M. S. & Alvarado, V. 2009 Flow of oil–water emulsions through a constricted capillary. Intl J. Multiphase Flow 35, 507–515.Google Scholar
Cristini, V., Bławzdziewicz, J. & Loewenberg, M. 1998 Drop breakup in three-dimensional viscous flows. Phys. Fluids 10, 1781–1783.Google Scholar
Cristini, V., Bławzdziewicz, J. & Loewenberg, M. 2001 An adaptive mesh algorithm for evolving surfaces: simulations of drop breakup and coalescence. J. Comput. Phys. 168, 445–463.Google Scholar
Cristini, V., Bławzdziewicz, J., Loewenberg, M. & Collins, L. R. 2003 Breakup in stochastic Stokes flows: sub-Kolmogorov drops in isotropic turbulence. J. Fluid Mech. 492, 231–250.CrossRefGoogle Scholar
Dupin, M. M., Halliday, I., Care, C. M., Alboul, L. & Munn, L. L. 2007 Modelling the flow of dense suspensions of deformable particles in three dimensions. Phys. Rev. E 75, 066707.Google Scholar
Eggers, J. 1997 Nonlinear dynamics and breakup of free-surface flows. Rev. Mod. Phys. 69, 865–929.CrossRefGoogle Scholar
Farrell, G. R., Martini, K. M. & Menon, N. 2010 Loose packings of frictional spheres. Soft Matt. 6, 2925–2930.CrossRefGoogle Scholar
Graham, D. R. & Higdon, J. J. L. 2000a Oscillatory flow of droplets in capillary tubes. Part 1. Straight tubes. J. Fluid Mech. 425, 31–53.CrossRefGoogle Scholar
Graham, D. R. & Higdon, J. J. L. 2000b Oscillatory flow of droplets in capillary tubes. Part 2. Constricted tubes. J. Fluid Mech. 425, 55–77.Google Scholar
Guillen, V R., Carvalho, M. S. & Alvarado, V. 2012 Pore scale and macroscopic displacement mechanisms in emulsion flooding. Transp. Porous Med. 94, 197–206.Google Scholar
Hasimoto, H. 1959 On the periodic fundamental solutions of the Stokes equations and their application to viscous flow past a cubic array of spheres. J. Fluid Mech. 5, 317–328.Google Scholar
Hebeker, F.-K. 1986 Efficient boundary element methods for three-dimensional exterior viscous flow. Numer. Meth. PDE 2, 273–297.CrossRefGoogle Scholar
Hernández-Ortiz, J. P., de Pablo, J. J. & Graham, M. D. 2007 Fast computation of many-particle hydrodynamic and electrostatic interactions in a confined geometry. Phys. Rev. Lett. 98, 140602.Google Scholar
Hockney, R. W. & Eastwood, J. W. 1981 Computer Simulation Using Particles. McGraw-Hill.Google Scholar
Jaiswal, A. K., Sundararajan, T. & Chhabra, R. P. 1993 Slow non-Newtonian flow through packed beds: effect of zero shear viscosity. Can. J. Chem. Engng 71, 646–651.Google Scholar
Kim, S. & Karilla, S. 1991 Microhydrodynamics: Principles and Selected Aplications. Butterworth-Heinemann.Google Scholar
Kozicki, W. 2001 Viscoeleastic flow in packed beds or porous media. Can. J. Chem. Eng. 79, 124–131.CrossRefGoogle Scholar
Ladd, A. J. C. 1990 Hydrodynamic transport coefficients of random dispersions of hard spheres. J. Chem. Phys. 93, 3484–3494.Google Scholar
Loewenberg, M. 1998 Numerical simulation of concentrated emulsion flows. Trans. ASME: J. Fluids Engng 120, 824–832.Google Scholar
Loewenberg, M. & Hinch, E. J. 1996 Numerical simulation of a concentrated emulsion in shear flow. J. Fluid Mech. 321, 395–419.CrossRefGoogle Scholar
MacMeccan, R. M., Clausen, J. R., Neitzel, G. P. & Aidun, C. K. 2009 Simulating deformable particle suspensions using a coupled lattice–Boltzmann and finite-element method. J. Fluid Mech. 618, 13–39.Google Scholar
Mo, G. & Sangani, A. S. 1994 A method for computing Stokes flow interactions among spherical objects and its application to suspensions of drops and porous particles. Phys. Fluids 6, 1637–1652.Google Scholar
Nemer, M. 2003 Near-contact motion of liquid drops in emulsions and foams. PhD thesis, Yale University, USA.Google Scholar
Nemer, M. B., Chen, X., Papadopoulos, D. H., Bławzdziewicz, J. & Loewenberg, M. 2004 Hindered and enhanced coalescence of drops in Stokes flow. Phys. Rev. Lett. 92, 114501.Google Scholar
Onoda, G. Y. & Liniger, E. G. 1990 Random loose packings of uniform sheres and the dilatancy onset. Phys. Rev. Lett. 64, 2727–2730.Google Scholar
Piri, M. & Blunt, M. J. 2005 Three-dimensional mixed-wet random pore-scale network modelling of two- and three-phase flow in porous media. I. Model description. Phys. Rev. E 71, 026301.Google Scholar
Power, H. & Miranda, G. 1987 Second kind integral equation formulation of Stokes flow past a particle of arbitrary shape. SIAM J. Appl. Maths 47, 689–698.Google Scholar
Pranay, P., Henríquez-Rivera, R. G. & Graham, M. D. 2012 Depletion layer formation in suspensions of elastic capsules in Newtonian and viscoelastic fluids. Phys. Fluids 24, 061902.Google Scholar
Quan, S., Lou, J. & Schmidt, D. P. 2009a Modelling merging and breakup in the moving mesh interface tracking method for multiphase flow simulations. J. Comput. Phys. 228, 2660–2675.Google Scholar
Quan, S. & Schmidt, D. P. 2007 A moving mesh interface tracking method for three-dimensional incompressible two-phase flows. J. Comput. Phys. 221, 761–780.CrossRefGoogle Scholar
Quan, S., Schmidt, D. P., Hua, J. & Lou, J. 2009b A numerical study of the relaxation and breakup of an elongated drop in a viscous liquid. J. Fluid Mech. 640, 235–264.Google Scholar
Rallison, J. M. 1981 A numerical study of the deformation and burst of a viscous drop in general shear flows. J. Fluid Mech. 109, 465–482.Google Scholar
Romero, M. I. & Carvalho, M. S. 2011 Experiments and network model of flow of oil-water emulsion in porous media. Phys. Rev. E 84, 046305.Google Scholar
Sangani, A. S. & Acrivos, A. 1982 Slow flow through a periodic array of spheres. Intl J. Multiphase Flow 8, 343–360.Google Scholar
Sangani, A. S. & Mo, G. 1996 An $O(N)$ algorithm for Stokes and Laplace interactions of particles. Phys. Fluids 8, 1990–2010.CrossRefGoogle Scholar
Scott, G. D. & Kilgour, D. M. 1969 The density of random close packing of spheres. Brit. J. Appl. Phys. Ser. 2 2, 863–866.Google Scholar
Secomb, T. W. 1995 Mechanics of blood flow in the microcirculation. In Biological Fluid Dynamics (ed. Ellington, C. P. & Pedley, T. J.). pp. 305–321.Google Scholar
Seo, J. H., Lele, S. K. & Tryggvason, G. 2010 Investigation and modelling of bubble–bubble interaction effect in homogeneous bubbly flows. Phys. Fluids 22, 063302.Google Scholar
Silbert, L. E. 2010 Jamming of frictional spheres and random loose packing. Soft Matt. 6, 2918–2924.CrossRefGoogle Scholar
Thomas, S., Esmaeeli, A. & Tryggvason, G. 2010 Multiscale computations of thin films in multiphase flows. Intl J. Multiphase Flow 36, 71–77.Google Scholar
Thompson, K. E. & Fogler, H. S. 1997 Modelling flow in disordered packed beds from pore-scale fluid mechanics. AIChE J. 43, 1377–1389.Google Scholar
Torquato, S. 2002 Random Heterogeneous Materials: Microstructure and Macroscopic Properties. Springer.Google Scholar
Tryggvason, G., Bunner, B., Esmaeeli, A., Juric, D., Al-rawahi, N., Tauber, W., Han, J., Nas, S. & Jan, Y.-J. 2001 A front-tracking method for the computations of multiphase flow. J. Comput. Phys. 169, 708–759.Google Scholar
Unverdi, S. O. & Tryggvason, G. 1992 A front-tracking method for viscous, incompressible, multi-fluid flows. J. Comput. Phys. 100, 25–37.Google Scholar
Zhang, H. P. & Makse, H. A. 2005 Jamming transition in emulsions and granular materials. Phys. Rev. E 72, 011301.Google Scholar
Zhu, J. & Satish, M. G. 1992 Non-Newtonian effects on the drag of creeping flow through packed beds. Intl J. Multiphase Flow 18, 765–777.Google Scholar
Zick, A. A. & Homsy, G. M. 1982 Stokes flow through periodic arrays of spheres. J. Fluid Mech. 115, 13–26.Google Scholar
Zinchenko, A. Z. 1994 Algorithm for random close packing of spheres with periodic boundary conditions. J. Comput. Phys. 114, 298–307.CrossRefGoogle Scholar
Zinchenko, A. Z. 1998 Effective conductivity of loaded granular materials by numerical simulation. Phil. Trans. R. Soc. Lond. A 356, 2953–2998.Google Scholar
Zinchenko, A. Z. & Davis, R. H. 2000 An efficient algorithm for hydrodynamical interaction of many deformable drops. J. Comput. Phys. 157, 539–587.Google Scholar
Zinchenko, A. Z. & Davis, R. H. 2002 Shear flow of highly concentrated emulsions of deformable drops by numerical simulations. J. Fluid Mech. 455, 21–62.Google Scholar
Zinchenko, A. Z. & Davis, R. H. 2003 Large-scale simulations of concentrated emulsion flows. Phil. Trans. R. Soc. Lond. A 361, 813–845.Google Scholar
Zinchenko, A. Z. & Davis, R. H. 2005 A multipole-accelerated algorithm for close interaction of slightly deformable drops. J. Comput. Phys. 207, 695–735.Google Scholar
Zinchenko, A. Z. & Davis, R. H. 2006 A boundary-integral study of a drop squeezing through interparticle constrictions. J. Fluid Mech. 564, 227–266.CrossRefGoogle Scholar
Zinchenko, A. Z. & Davis, R. H. 2008a Algorithm for direct numerical simulation of emulsion flow through a granular material. J. Comput. Phys. 227, 7841–7888.Google Scholar
Zinchenko, A. Z. & Davis, R. H. 2008b Squeezing of a periodic emulsion through a cubic lattice of spheres. Phys. Fluids 20, 040803.CrossRefGoogle Scholar
Zinchenko, A. Z., Rother, M. A. & Davis, R. H. 1997 A novel boundary-integral algorithm for viscous interaction of deformable drops. Phys. Fluids 9, 1493–1511.Google Scholar