Hostname: page-component-586b7cd67f-rdxmf Total loading time: 0 Render date: 2024-11-23T01:49:52.289Z Has data issue: false hasContentIssue false
  • English
  • Français

Elliptical instability of the Moore–Saffman model for a trailing wingtip vortex

Published online by Cambridge University Press:  30 August 2016

J. Feys  and
S. A. Maslowe
J. Feys*
Affiliation:
Department of Mathematics and Statistics, McGill University, Montreal, Quebec H3A 0B9, Canada
S. A. Maslowe
Affiliation:
Department of Mathematics and Statistics, McGill University, Montreal, Quebec H3A 0B9, Canada
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

In this paper, we investigate the elliptical instability exhibited by two counter-rotating trailing vortices. This type of instability can be viewed as a resonance between two normal modes of a vortex and an external strain field. Recent numerical investigations have extended earlier results that ignored axial flow to include models with a simple wake-like axial flow such as the similarity solution found by Batchelor (J. Fluid Mech., vol. 20, 1964, pp. 645–658). We present herein growth rates of elliptical instability for a family of velocity profiles found by Moore & Saffman (Proc. R. Soc. Lond. A, vol. 333, 1973, pp. 491–508). These profiles have a parameter $n$ that depends on the wing loading. As a result, unlike the Batchelor vortex, they are capable of modelling both the jet-like and the wake-like axial flow present in a trailing vortex at short and intermediate distances behind a wingtip. Direct numerical simulations of the linearized Navier–Stokes equations are performed using an efficient spectral method in cylindrical coordinates developed by Matsushima & Marcus (J. Comput. Phys., vol. 53, 1997, pp. 321–345). We compare our results with those for the Batchelor vortex, whose velocity profiles are closely approximated as the wing loading parameter $n$ approaches 1. An important conclusion of our investigation is that the stability characteristics vary considerably with $n$ and 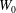$W_{0}$, a parameter measuring the strength of the mean axial velocity component. In the case of an elliptically loaded wing (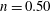$n=0.50$), we find that the instability growth rates are up to 50 % greater than those for the Batchelor vortex. Our results demonstrate the significant effect of the distribution and intensity of the axial flow on the elliptical instability of a trailing vortex.

JFM classification

Vortex Flows: Vortex Flows Vortex Flows: Vortex instability Vortex Flows: Vortex interactions
Type
Papers
Information
Journal of Fluid Mechanics , Volume 803 , 25 September 2016 , pp. 556 - 590
Check for updates
Copyright
© 2016 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Abramowitz, M. & Stegun, I. A. 1972 Handbook of Mathematical Functions. Dover.Google Scholar
Anderson, E. A. & Lawton, T. A. 2003 Correlation between vortex strength and axial velocity in a trailing vortex. J. Aircraft 40, 699–704.Google Scholar
Ash, R. L. & Khorrami, M. R. 1995 Vortex stability. In Fluid Vortices (ed. Green, S. I.), pp. 317–372. Kluwer.Google Scholar
Baker, G. R., Barker, S. J., Bofah, K. K. & Saffman, P. G. 1974 Laser anemometer measurements of trailing vortices in water. J. Fluid Mech. 65, 325–336.Google Scholar
Batchelor, G. K. 1964 Axial flow in trailing line vortices. J. Fluid Mech. 20, 645–658.Google Scholar
Bayly, B. J. 1986 Three-dimensional instability of elliptical flow. Phys. Rev. Lett. 57, 2160–2163.Google Scholar
Boyd, J. P. 2000 Chebyshev and Fourier Spectral Methods. Dover.Google Scholar
Bristol, R. L., Ortega, J. M., Marcus, P. S. & Savaş, Ö. 2004 On cooperative instabilities of parallel vortex pairs. J. Fluid Mech. 517, 331–358.Google Scholar
Brown, A. P.2014 The alleviation of wake vortex encounter loads, a study of flight research data. AIAA Paper 2014-2337.Google Scholar
Cain, A. B., Ferziger, J. H. & Reynolds, W. C. 1984 Discrete orthogonal function expansions for non-uniform grids using the fast Fourier transform. J. Comput. Phys. 56, 272–286.Google Scholar
Chow, J. S., Zilliac, G. G. & Bradshaw, P. 1997 Mean and turbulence measurements in the near field of a wing-tip vortex. AIAA J. 35, 1561–1567.Google Scholar
Devenport, W. J., Rife, M. C., Liapis, S. I. & Follin, G. J. 1996 The structure and development of a wingtip vortex. J. Fluid Mech. 312, 67–106.Google Scholar
Eloy, C. & Le Dizès, S. 2001 Stability of the Rankine vortex in a multipolar strain field. Phys. Fluids 13, 660–676.Google Scholar
Fabre, D. & Jacquin, L. 2004a Short-wave cooperative instabilities in representative aircraft vortices. Phys. Fluids 16, 1366–1378.Google Scholar
Fabre, D. & Jacquin, L. 2004b Viscous instabilities in trailing vortices at large swirl numbers. J. Fluid Mech. 500, 239–262.Google Scholar
Fabre, D., Sipp, D. & Jacquin, L. 2006 Kelvin waves and the singular modes of the Lamb–Oseen vortex. J. Fluid Mech. 551, 235–274.Google Scholar
Faddy, J. M.2005 Flow structure in a model of aircraft trailing vortices. PhD thesis, California Institute of Technology.Google Scholar
Faddy, J. M. & Pullin, D. I. 2005 Flow structure in a model of aircraft trailing vortices. Phys. Fluids 17, 085106.Google Scholar
Feys, J. & Maslowe, S. A. 2014 Linear stability of the Moore–Saffman model for a trailing wingtip vortex. Phys. Fluids 26, 024108.Google Scholar
Fukumoto, Y. 2003 The three-dimensional instability of a strained vortex tube revisited. J. Fluid Mech. 493, 287–318.Google Scholar
Gottlieb, D. & Orszag, S. A. 1977 Numerical Analysis of Spectral Methods: Theory and Applications. SIAM.Google Scholar
Heaton, C. J. 2007a Centre modes in inviscid swirling flows and their application to the stability of the Batchelor vortex. J. Fluid Mech. 576, 325–348.Google Scholar
Heaton, C. J. 2007b Optimal growth of the Batchelor vortex viscous modes. J. Fluid Mech. 592, 495–505.Google Scholar
Jiménez, J., Moffatt, H. K. & Vasco, C. 1996 The structure of the vortices in freely decaying two-dimensional turbulence. J. Fluid Mech. 313, 209–222.Google Scholar
Karniadakis, G. E., Israeli, M. & Orszag, S. A. 1991 High-order splitting methods for the incompressible Navier–Stokes equations. J. Comput. Phys. 97, 414–443.Google Scholar
Kerswell, R. R. 2002 Elliptical instability. Annu. Rev. Fluid Mech. 34, 83–113.Google Scholar
Khorrami, M. R. 1991 On the viscous modes of instability of a trailing line vortex. J. Fluid Mech. 225, 197–212.Google Scholar
Lacaze, L., Birbaud, A.-L. & Le Dizès, S. 2005 Elliptical instability in a Rankine vortex with axial flow. Phys. Fluids 17, 017101.Google Scholar
Lacaze, L., Ryan, K. & Le Dizès, S. 2007 Elliptical instability in a strained Batchelor vortex. J. Fluid Mech. 577, 341–361.Google Scholar
Landman, M. J. & Saffman, P. G. 1987 The three-dimensional instability of strained vortices in a viscous fluid. Phys. Fluids 30, 2339–2342.Google Scholar
Le Dizès, S. 2004 Viscous critical-layer analysis of vortex normal modes. Stud. Appl. Maths 112, 315–332.Google Scholar
Le Dizès, S. & Laporte, F. 2002 Theoretical predictions for the elliptical instability in a two-vortex flow. J. Fluid Mech. 471, 169–201.Google Scholar
Lessen, M., Singh, P. J. & Paillet, F. 1974 The stability of a trailing line vortex. Part 1. Inviscid theory. J. Fluid Mech. 63, 753–763.Google Scholar
Mao, X.2010 Vortex instability and transient growth. PhD thesis, Imperial College London.Google Scholar
Matsushima, T. & Marcus, P. S. 1997 A spectral method for unbounded domains. J. Comput. Phys. 53, 321–345.Google Scholar
Mayer, E. W. & Powell, K. G. 1992 Viscous and inviscid instabilities of a trailing vortex. J. Fluid Mech. 245, 91–114.Google Scholar
Moore, D. W. & Saffman, P. G. 1973 Axial flow in laminar trailing vortices. Proc. R. Soc. Lond. A 333, 491–508.Google Scholar
Moore, D. W. & Saffman, P. G. 1975 The instability of a straight vortex filament in a strain field. Proc. R. Soc. Lond. A 346, 413–425.Google Scholar
Nomura, K. K., Tsutsui, H., Mahoney, D. & Rottman, J. W. 2006 Short-wavelength instability and decay of a vortex pair in a stratified fluid. J. Fluid Mech. 553, 283–322.Google Scholar
Phillips, W. R. C. 1981 The turbulent trailing vortex during roll-up. J. Fluid Mech. 105, 451–467.Google Scholar
Pierrehumbert, R. T. 1986 Universal short-wave instability of two-dimensional eddies in an inviscid fluid. Phys. Rev. Lett. 57, 2157–2160.Google Scholar
del Pino, C., Parras, L., Felli, M. & Fernandez-Feria, R. 2011 Structure of trailing vortices: comparison between particle image velocimetry measurements and theoretical models. Phys. Fluids 23, 013602.Google Scholar
Roy, C., Leweke, T., Thompson, M. C. & Hourigan, K. 2011 Experiments on the elliptic instability in vortex pairs with axial core flow. J. Fluid Mech. 677, 383–416.Google Scholar
Roy, C., Schaeffer, N., Le Dizès, S. & Thompson, M. 2008 Stability of a pair of co-rotating vortices with axial flow. Phys. Fluids 20, 094101.Google Scholar
Saffman, P. G. 1992 Vortex Dynamics. Cambridge University Press.Google Scholar
Sakai, T. & Redekopp, L. G. 2009 An application of one-sided Jacobi polynomials for spectral modeling of vector fields in polar coordinates. J. Comput. Phys. 228, 7069–7085.Google Scholar
Sipp, D. & Jacquin, L. 2003 Widnall instabilities in vortex pairs. Phys. Fluids 15 (7), 1861–1874.Google Scholar
Spalart, P. R. 1998 Airplane trailing vortices. Annu. Rev. Fluid Mech. 30, 107–138.Google Scholar
Tsai, C.-Y. & Widnall, S. E. 1976 The stability of short waves on a straight vortex filament in a weak externally imposed strain field. J. Fluid Mech. 73, 721–733.Google Scholar
Waleffe, F. 1990 On the three-dimensional instability of strained vortices. Phys. Fluids A 2, 76–80.Google Scholar
Widnall, S. E., Bliss, D. B. & Tsai, C.-Y. 1974 The instability of short waves on a vortex ring. J. Fluid Mech. 66, 35–47.Google Scholar