Hostname: page-component-cd9895bd7-dzt6s Total loading time: 0 Render date: 2024-12-25T13:35:22.017Z Has data issue: false hasContentIssue false
  • English
  • Français

Elastohydrodynamics of contact in adherent sheets

Published online by Cambridge University Press:  22 August 2022

Stéphane Poulain Open the ORCID record for Stéphane Poulain [Opens in a new window] ,
Andreas Carlson Open the ORCID record for Andreas Carlson [Opens in a new window] ,
Shreyas Mandre Open the ORCID record for Shreyas Mandre [Opens in a new window]  and
L. Mahadevan Open the ORCID record for L. Mahadevan [Opens in a new window]
Stéphane Poulain
Affiliation:
Mechanics Division, Department of Mathematics, University of Oslo, 0316 Oslo, Norway
Andreas Carlson
Affiliation:
Mechanics Division, Department of Mathematics, University of Oslo, 0316 Oslo, Norway
Shreyas Mandre
Affiliation:
Mathematics Institute, University of Warwick, Coventry CV4 7AL, UK
L. Mahadevan*
Affiliation:
Paulson School of Engineering and Applied Sciences, Department of Physics, Harvard University, Cambridge, MA 02138, USA Department of Organismic and Evolutionary Biology, Harvard University, Cambridge, MA 02138, USA
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

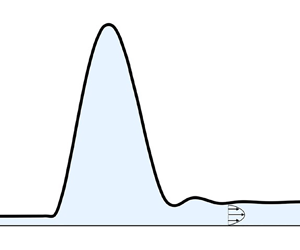
Adhesive contact between a thin elastic sheet and a substrate arises in a range of biological, physical and technological applications. By considering the dynamics of this process that naturally couples fluid flow, long-wavelength elastic deformations and microscopic adhesion, we analyse a sixth-order thin-film equation for the short-time dynamics of the onset of adhesion and the long-time dynamics of a steadily propagating adhesion front. Numerical solutions corroborate scaling laws and asymptotic analyses for the characteristic waiting time for adhesive contact and for the speed of the adhesion front. A similarity analysis of the governing partial differential equation further allows us to determine the shape of a fluid-filled blister ahead of the adhesion front. Finally, our analysis reveals a near-singular behaviour at the moving elastohydrodynamic contact line with an effective boundary condition that might be useful in other related problems.

JFM classification

Interfacial Flows (free surface): Thin films Low-Reynolds-number flows: Lubrication theory
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 947 , 25 September 2022 , A16
Check for updates
Copyright
© The Author(s), 2022. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

Ball, T.V. & Neufeld, J.A. 2018 Static and dynamic fluid-driven fracturing of adhered elastica. Phys. Rev. Fluids 3 (7), 074101.CrossRefGoogle Scholar
Batchelor, G.K. 1967 An Introduction to Fluid Dynamics. Cambridge University Press.Google Scholar
Bell, G.I. 1978 Models for the specific adhesion of cells to cells. Science 200 (4342), 618–627.CrossRefGoogle ScholarPubMed
Bell, G.I., Dembo, M. & Bongrand, P. 1984 Cell adhesion, competition between nonspecific repulsion and specific bonding. Biophys. J. 45 (6), 1051–1064.CrossRefGoogle ScholarPubMed
Bengtsson, S., Ljungberg, K. & Vedde, J. 1996 The influence of wafer dimensions on the contact wave velocity in silicon wafer bonding. Appl. Phys. Lett. 69 (22), 3381–3383.CrossRefGoogle Scholar
Berhanu, M., Guérin, A., Courrech du Pont, S., Raoult, F., Perrier, R. & Michaut, C. 2019 Uplift of an elastic membrane by a viscous flow. Phys. Rev. E 99 (4), 043102.CrossRefGoogle ScholarPubMed
de Boer, M.P. & de Boer, P.C.T. 2007 Thermodynamics of capillary adhesion between rough surfaces. J. Colloid Interface Sci. 311 (1), 171–185.CrossRefGoogle ScholarPubMed
Bongrand, P. 1988 Physical Basis of Cell-Cell adhesion. CRC Press.Google Scholar
Bonn, D., Eggers, J., Indekeu, J., Meunier, J. & Rolley, E. 2009 Wetting and spreading. Rev. Mod. Phys. 81 (2), 739–805.CrossRefGoogle Scholar
Butler, M., Box, F., Robert, T. & Vella, D. 2019 Elasto-capillary adhesion: effect of deformability on adhesion strength and detachment. Phys. Rev. Fluids 4, 033601.CrossRefGoogle Scholar
Cantat, I. & Misbah, C. 1999 Dynamics and similarity laws for adhering vesicles in haptotaxis. Phys. Rev. Lett. 83 (1), 235–238.CrossRefGoogle Scholar
Carlson, A. 2018 Fluctuation assisted spreading of a fluid filled elastic blister. J. Fluid Mech. 846, 1076–1087.CrossRefGoogle Scholar
Carlson, A., Kim, P., Amberg, G. & Stone, H.A. 2013 Short and long time drop dynamics on lubricated substrates. Europhys. Lett. 104 (3), 34008.CrossRefGoogle Scholar
Carlson, A. & Mahadevan, L. 2016 Similarity and singularity in adhesive elastohydrodynamic touchdown. Phys. Fluids 28 (1), 011702.CrossRefGoogle Scholar
Dirks, J.-H. 2014 Physical principles of fluid-mediated insect attachment – shouldn't insects slip? Beilstein J. Nanotechnol. 5 (1), 1160–1166.CrossRefGoogle ScholarPubMed
Eggers, J. 2005 Contact line motion for partially wetting fluids. Phys. Rev. E 72 (6), 061605.CrossRefGoogle ScholarPubMed
Flitton, J.C. & King, J.R. 2004 Moving-boundary and fixed-domain problems for a sixth-order thin-film equation. Eur. J. Appl. Maths 15 (6), 713–754.CrossRefGoogle Scholar
Fournel, F., Martin-Cocher, C., Radisson, D., Larrey, V., Beche, E., Morales, C., Delean, P.A., Rieutord, F. & Moriceau, H. 2015 Water stress corrosion in bonded structures. ECS J. Solid State Sci. Technol. 4 (5), P124–P130.CrossRefGoogle Scholar
de Gennes, P.-G. 1985 Wetting: statics and dynamics. Rev. Mod. Phys. 57 (3), 827–863.CrossRefGoogle Scholar
Han, W., Yu, J. & Wang, Q. 2000 Modeling the dynamics of si wafer bonding during annealing. J. Appl. Phys. 88 (7), 4404–4406.CrossRefGoogle Scholar
Hewitt, I.J., Balmforth, N.J. & De Bruyn, J.R. 2015 Elastic-plated gravity currents. Eur. J. Appl. Maths 26 (1), 1–31.CrossRefGoogle Scholar
Hosoi, A.E. & Mahadevan, L. 2004 Peeling, healing, and bursting in a lubricated elastic sheet. Phys. Rev. Lett. 93 (13), 137802.CrossRefGoogle Scholar
Israelachvili, J.N. 2011 Intermolecular and Surface Forces. Academic Press.Google Scholar
Juel, A., Pihler-Puzović, D. & Heil, M. 2018 Instabilities in blistering. Annu. Rev. Fluid Mech. 50, 691–714.CrossRefGoogle Scholar
Kavanagh, J.L., Engwell, S.L. & Martin, S.A. 2018 A review of laboratory and numerical modelling in volcanology. Solid Earth 9 (2), 531–571.CrossRefGoogle Scholar
Landau, L.D. & Lifshitz, E.M. 1986 Course of Theoretical Physics vol. 7: Theory of Elasticity. 3rd edn. Pergamon.Google Scholar
Leong, F.Y. & Chiam, K.-H. 2010 Adhesive dynamics of lubricated films. Phys. Rev. E 81 (4), 041923.CrossRefGoogle ScholarPubMed
Lister, J.R., Peng, G.G. & Neufeld, J.A. 2013 Viscous control of peeling an elastic sheet by bending and pulling. Phys. Rev. Lett. 111 (15), 154501.CrossRefGoogle Scholar
Lister, J.R., Skinner, D.J. & Large, T.M.J. 2019 Viscous control of shallow elastic fracture: peeling without precursors. J. Fluid Mech. 868, 119–140.CrossRefGoogle Scholar
Longley, J.E., Mahadevan, L. & Chaudhury, M.K. 2013 How a blister heals. Europhys. Lett. 104 (4), 46002.CrossRefGoogle Scholar
Majidi, C. & Adams, G.G. 2009 A simplified formulation of adhesion problems with elastic plates. Proc. R. Soc. A 465 (2107), 2217–2230.CrossRefGoogle Scholar
Mani, M., Gopinath, A. & Mahadevan, L. 2012 How things get stuck: kinetics, elastohydrodynamics, and soft adhesion. Phys. Rev. Lett. 108 (22), 226104.CrossRefGoogle ScholarPubMed
Michaut, C. 2011 Dynamics of magmatic intrusions in the upper crust: theory and applications to laccoliths on earth and the moon. J. Geophys. Res. 116 (B5), B05205.Google Scholar
Moriceau, H., Rieutord, F., Fournel, F., Le Tiec, Y., Di Cioccio, L., Morales, C., Charvet, A.M. & Deguet, C. 2011 Overview of recent direct wafer bonding advances and applications. Adv. Nat. Sci. 1 (4), 043004.Google Scholar
Navarro, E., Bréchet, Y., Moreau, R., Pardoen, T., Raskin, J.-P., Barthelemy, A. & Radu, I. 2013 Direct silicon bonding dynamics: a coupled fluid/structure analysis. Appl. Phys. Lett. 103 (3), 034104.CrossRefGoogle Scholar
Obreimoff, J.W. 1930 The splitting strength of mica. Proc. R. Soc. A 127 (805), 290–297.Google Scholar
Oron, A., Davis, S.H. & Bankoff, S.G. 1997 Long-scale evolution of thin liquid films. Rev. Mod. Phys. 69 (3), 931–980.CrossRefGoogle Scholar
Pedersen, C., Niven, J.F., Salez, T., Dalnoki-Veress, K. & Carlson, A. 2019 Asymptotic regimes in elastohydrodynamic and stochastic leveling on a viscous film. Phys. Rev. Fluids 4, 124003.CrossRefGoogle Scholar
Peng, G.G. & Lister, J.R. 2020 Viscous flow under an elastic sheet. J. Fluid Mech. 905, A30.CrossRefGoogle Scholar
Peng, G.G., Pihler-Puzovic, D., Juel, A., Heil, M. & Lister, J.R. 2015 Displacement flows under elastic membranes. Part 2. Analysis of interfacial effects. J. Fluid Mech. 784, 512–547.CrossRefGoogle Scholar
Pihler-Puzović, D., Illien, P., Heil, M. & Juel, A. 2012 Suppression of complex fingerlike patterns at the interface between air and a viscous fluid by elastic membranes. Phys. Rev. Lett. 108 (7), 074502.CrossRefGoogle Scholar
Pocius, A.V. & Dillard, D.A. 2002 Adhesion Science and Engineering: Surfaces, Chemistry and Applications. Elsevier.Google Scholar
Radisson, D., Fournel, F. & Charlaix, E. 2015 Modelling of the direct bonding wave. Microsyst. Technol. 21 (5), 969–971.CrossRefGoogle Scholar
Rieutord, F., Bataillou, B. & Moriceau, H. 2005 Dynamics of a bonding front. Phys. Rev. Lett. 94 (23), 236101.CrossRefGoogle ScholarPubMed
Rieutord, F., Moriceau, H., Beneyton, R., Capello, L., Morales, C. & Charvet, A.-M. 2006 Rough surface adhesion mechanisms for wafer bonding. ECS Trans. 3 (6), 205–215.CrossRefGoogle Scholar
Rieutord, F., Rauer, C. & Moriceau, H. 2014 Interfacial closure of contacting surfaces. Europhys. Lett. 107 (3), 34003.CrossRefGoogle Scholar
Salem, L., Gamus, B., Or, Y. & Gat, A.D. 2020 Leveraging viscous peeling to create and activate soft actuators and microfluidic devices. Soft Robot. 7 (1), 76–84.CrossRefGoogle ScholarPubMed
Snoeijer, J.H. & Andreotti, B. 2013 Moving contact lines: scales, regimes, and dynamical transitions. Annu. Rev. Fluid Mech. 45, 269–292.CrossRefGoogle Scholar
Snoeijer, J.H. & Eggers, J. 2010 Asymptotic analysis of the dewetting rim. Phys. Rev. E 82, 056314.CrossRefGoogle ScholarPubMed
Springman, R.M. & Bassani, J.L. 2008 Snap transitions in adhesion. J. Mech. Phys. Solids 56 (6), 2358–2380.CrossRefGoogle Scholar
Springman, R.M. & Bassani, J.L. 2009 Mechano-chemical coupling in the adhesion of thin-shell structures. J. Mech. Phys. Solids 57 (6), 909–931.CrossRefGoogle Scholar
Tong, Q.-Y. & Gösele, U. 1999 Semiconductor Wafer Bonding: Science and Technology. John Wiley.Google Scholar
Turner, K.T., Thouless, M.D. & Spearing, S.M. 2004 Mechanics of wafer bonding: effect of clamping. J. Appl. Phys. 95 (1), 349–355.CrossRefGoogle Scholar
Wang, Z.-Q. & Detournay, E. 2018 The tip region of a near-surface hydraulic fracture. J. Appl. Mech. 85 (4), 041010.CrossRefGoogle Scholar
Wang, Z.-Q. & Detournay, E. 2021 Force on a moving liquid blister. J. Fluid Mech. 918, A15.CrossRefGoogle Scholar
Zhang, W.W. & Lister, J.R. 1999 Similarity solutions for van der Waals rupture of a thin film on a solid substrate. Phys. Fluids 11 (9), 2454–2462.CrossRefGoogle Scholar