Hostname: page-component-586b7cd67f-t7fkt Total loading time: 0 Render date: 2024-11-26T19:59:49.875Z Has data issue: false hasContentIssue false
  • English
  • Français

Elasto-capillary coalescence of multiple parallel sheets

Published online by Cambridge University Press:  16 April 2013

A. D. Gat  and
M. Gharib
A. D. Gat*
Affiliation:
Graduate Aerospace Laboratories, California Institute of Technology, Pasadena, CA 91125, USA
M. Gharib
Affiliation:
Graduate Aerospace Laboratories, California Institute of Technology, Pasadena, CA 91125, USA
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We analyse two-dimensional clamped parallel elastic sheets which are partially immersed in liquid as a model for elasto-capillary coalescence. In the existing literature this problem is studied via minimal energy analysis of capillary and elastic energies of the post-coalescence state, yielding the maximal stable post-coalescence bundle size. Utilizing modal stability analysis and asymptotic analysis, we studied the stability of the configuration before the coalescence occurred. Our analysis revealed previously unreported relations between viscous forces, body forces, and the instability yielding the coalescence, thus undermining a common assumption that coalescence will occur as long as it will not create a bundle larger than the maximal stable post-coalesced size. A mathematical description of the process creating the hierarchical coalescence structure was obtained and yielded that the mean number of sheets per coalesced region is limited to the subset 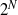${2}^{N} $ where 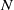$N$ is the set of natural numbers. Our theoretical results were illustrated by experiments and good agreement with the theoretical predictions was observed.

JFM classification

Instability: Instability Interfacial Flows (free surface): Interfacial Flows (free surface) Low-Reynolds-number flows: Low-Reynolds-number flows
Type
Papers
Information
Journal of Fluid Mechanics , Volume 723 , 25 May 2013 , pp. 692 - 705
Copyright
©2013 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Antkowiak, A., Audoly, B., Josserand, C., Neukirch, S. & Rivetti, M. 2011 Instant fabrication and selection of folded structures using drop impact. Proc. Natl Acad. Sci. 108, 10400–10404.CrossRefGoogle ScholarPubMed
Aristoff, J. M., Duprat, C. & Stone, H. A. 2011 Elastocapillary imbibition. Intl J. Non-Linear Mech. 46, 648–656.CrossRefGoogle Scholar
Bico, J., Roman, B., Moulin, L. & Boudaoud, A. 2004 Elastocapillary coalescence in wet hair. Nature 432, 690.Google Scholar
Boudaoud, A., Bico, J. & Roman, B. 2007 Elastocapillary coalescence: aggregation and fragmentation with a maximal size. Phys. Rev. E 76, 060102.Google Scholar
Chandra, D. & Yang, S. 2010 Stability of high-aspect-ratio micropillar arrays against adhesive and capillary forces. Acc. Chem. Res. 43, 1080–1091.Google Scholar
Chandra, D., Yang, S., Soshinsky, A. A. & Gambogi, R. J. 2009 Biomimetic ultrathin whitening by capillary-force-induced random clustering of hydrogel micropillar arrays. ACS Appl. Mater. Interfaces 1, 1698–1704.Google Scholar
Chiodi, F., Roman, B. & Bico, J. 2010 Piercing an interface with a brush: Collaborative stiffening. Europhys. Lett. 90, 044006.Google Scholar
De Gennes, P. G., Brochard-Wyart, F., Quéré, D., Reisinger, A. & Widom, B. 2004 Capillarity and Wetting Phenomena: Drops, Bubbles, Pearls, Waves. Springer.Google Scholar
De Volder, M., Tawfick, S. H., Park, S. J., Copic, D., Zhao, Z., Lu, W. & Hart, A. J. 2010 Diverse 3D microarchitectures made by capillary forming of carbon nanotubes. Adv. Mater. 22, 4384–4389.CrossRefGoogle ScholarPubMed
De Volder, M. F. L., Park, S. J., Tawfick, S. H., Vidaud, D. O. & Hart, A. J. 2011 Fabrication and electrical integration of robust carbon nanotube micropillars by self-directed elastocapillary densification. J. Micromech. Microengng 21, 045033.Google Scholar
Duan, H. & Berggren, K. K. 2010 Directed self-assembly at the 10 nm scale by using capillary force-induced nanocohesion. Nano Lett. 10, 3710–3716.Google Scholar
Duprat, C., Aristoff, J. M. & Stone, H. A. 2011 Dynamics of elastocapillary rise. J. Fluid Mech. 679, 641–654.Google Scholar
Duprat, C., Protire, S., Beebe, A. Y. & Stone, H. A. 2012 Wetting of flexible fibre arrays. Nature 482, 510–513.Google Scholar
Elwenspoek, M., Abelmann, L., Berenschot, E., van Honschoten, J., Jansen, H. & Tas, N. 2010 Self-assembly of (sub-)micron particles into supermaterials. J. Micromech. Microengng 20, 064001.Google Scholar
Gat, A., Navaz, H. & Gharib, M. 2011 Dynamics of freely moving plates connected by a shallow liquid bridge. Phys. Fluids 23 (9), 097101+.Google Scholar
Huang, X., Zhou, J., Sansom, E., Gharib, M. & Haur, S. C. 2007 Inherent opening controlled pattern formation in carbon nanotube arrays. Nanotechnology 18, 305301.Google Scholar
Journet, C., Moulinet, S., Ybert, C., Purcell, S. T. & Bocquet, L. 2005 Contact angle measurements on superhydrophobic carbon nanotube forests: effect of fluid pressure. Europhys. Lett. 71 (1), 104–109.Google Scholar
Kang, S. H., Wu, N., Grinthal, A. & Aizenberg, J. 2011 Meniscus lithography: evapouration-induced self-organization of pillar arrays into moir patterns. Phys. Rev. Lett. 107, 177802.Google Scholar
Kim, H.-Y. & Mahadevan, L. 2006 Capillary rise between elastic sheets. J. Fluid Mech. 548, 141–150.Google Scholar
Leal, G. 2007 Advanced Transport Phenomena: Fluid Mechanics and Convective Transport Processes. Cambridge Series in Chemical Engineering. Cambridge University Press.CrossRefGoogle Scholar
Liu, J.-L., Feng, X.-Q., Xia, R. & Zhao, H.-P. 2007 Hierarchical capillary adhesion of microcantilevers or hairs. J. Phys. D: Appl. Phys. 40, 5564–5570.Google Scholar
Pineirua, M., Bico, J. & Roman, B. 2010 Capillary origami controlled by an electric field. Soft Matt. 6, 4491–4496.Google Scholar
Pokroy, B, Kang, S. H., Mahadevan, L. & Aizenberg, J. 2009 Self-organization of a mesoscale bristle into ordered, hierarchical helical assemblies. Science 323, 237–240.CrossRefGoogle ScholarPubMed
Py, C., Bastien, R., Bico, J., Roman, B. & Boudaoud, A. 2007a 3D aggregation of wet fibres. Europhys. Lett. 77, 44005.Google Scholar
Py, C., Reverdy, P., Doppler, L., Bico, J., Roman, B. & Baroud, C. N. 2007b Capillary origami: spontaneous wrapping of a droplet with an elastic sheet. Phys. Rev. Lett. 98, 156103.Google Scholar
Sikalo, S., Tropea, C. & Ganic, E. 2005 Dynamic wetting angle of a spreading droplet. Exp. Therm. Fluid Sci. 29, 795.Google Scholar
Taroni, M. & Vella, D. 2012 Multiple equilibria in a simple elastocapillary system. J. Fluid Mech. 712, 273–294.Google Scholar
Zhao, Y.-P. & Fan, J.-G. 2006 Clusters of bundled nanorods in nanocarpet effect. Appl. Phys. Lett. 88, 103123.Google Scholar
Zhao, Z., Tawfick, S. H., Park, S. J., De Volder, M., Hart, A. J. & Lu, W. 2010 Bending of nanoscale filament assemblies by elastocapillary densification. Phys. Rev. E 82, 041605.Google Scholar