Hostname: page-component-586b7cd67f-vdxz6 Total loading time: 0 Render date: 2024-11-26T08:48:03.907Z Has data issue: false hasContentIssue false
  • English
  • Français

Effects of the air layer of an idealized superhydrophobic surface on the slip length and skin-friction drag

Published online by Cambridge University Press:  01 February 2016

Taeyong Jung ,
Haecheon Choi  and
John Kim
Taeyong Jung
Affiliation:
Department of Mechanical & Aerospace Engineering, Seoul National University, Seoul 08826, Korea
Haecheon Choi*
Affiliation:
Department of Mechanical & Aerospace Engineering, Seoul National University, Seoul 08826, Korea Institute of Advanced Machines and Design, Seoul National University, Korea
John Kim
Affiliation:
Department of Mechanical and Aerospace Engineering, University of California, Los Angeles, CA 90095, USA
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

The anisotropy of the slip length and its effect on the skin-friction drag are numerically investigated for a turbulent channel flow with an idealized superhydrophobic surface having an air layer, where the idealized air–water interface is flat and does not contain the surface-tension effect. Inside the air layer, both the shear-driven flow and recirculating flow with zero net mass flow rate are considered. With increasing air-layer thickness, the slip length, slip velocity and percentage of drag reduction increase. It is shown that the slip length is independent of the water flow and depends only on the air-layer geometry. 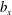The amount of drag reduction obtained is in between those by the empirical formulae from the streamwise slip only and isotropic slip, indicating that the present air–water interface generates an anisotropic slip, and the streamwise slip length ($b_{x}$) is larger than the spanwise one (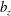$b_{z}$). From the joint probability density function of the slip velocities and velocity gradients at the interface, we confirm the anisotropy of the slip lengths and obtain their relative magnitude (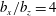$b_{x}/b_{z}=4$) for the present idealized superhydrophobic surface. It is also shown that the Navier slip model is valid only in the mean sense, and it is generally not applicable to fluctuating quantities.

JFM classification

Boundary Layers: Boundary layer control Flow Control: Drag reduction Turbulent Flows: Turbulence simulation
Type
Rapids
Information
Journal of Fluid Mechanics , Volume 790 , 10 March 2016 , R1
Check for updates
Copyright
© 2016 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Aljallis, E., Sarshar, M. A., Datla, R., Sikka, V., Jones, A. & Choi, C.-H. 2013 Experimental study of skin friction drag reduction on superhydrophobic flat plates in high Reynolds number boundary layer flow. Phys. Fluids 25, 025103.Google Scholar
Belyaev, A. V. & Vinogradova, O. I. 2010 Effective slip in pressure-driven flow past super-hydrophobic stripes. J. Fluid Mech. 652, 489–499.CrossRefGoogle Scholar
Busse, A. & Sandham, N. D. 2012 Influence of an anisotropic slip-length boundary condition on turbulent channel flow. Phys. Fluids 24, 055111.Google Scholar
Busse, A., Sandham, N. D., McHale, G. & Newton, M. I. 2013 Change in drag, apparent slip and optimum air layer thickness for laminar flow over an idealised superhydrophobic surface. J. Fluid Mech. 727, 488–508.Google Scholar
Daniello, R. J., Waterhouse, N. E. & Rothstein, J. P. 2009 Drag reduction in turbulent flows over superhydrophobic surfaces. Phys. Fluids 21, 085103.Google Scholar
Davies, J., Maynes, D., Webb, B. W. & Woolford, B. 2006 Laminar flow in a microchannel with superhydrophobic walls exhibiting transverse ribs. Phys. Fluids 18, 087110.Google Scholar
Fukagata, K., Kasagi, N. & Koumoutsakos, P. 2006 A theoretical prediction of friction drag reduction in turbulent flow by superhydrophobic surfaces. Phys. Fluids 18, 051703.Google Scholar
Hahn, S., Je, J. & Choi, H. 2002 Direct numerical simulation of turbulent channel flow with permeable walls. J. Fluid Mech. 450, 259–285.Google Scholar
Jelly, T. O., Jung, S. Y. & Zaki, T. A. 2014 Turbulence and skin friction modification in channel flow with streamwise-aligned superhydrophobic surface texture. Phys. Fluids 26, 095102.Google Scholar
Joseph, D. D. 1980 Boundary conditions for thin lubrication layers. Phys. Fluids 23, 2356.Google Scholar
Jung, Y. C. & Bhushan, B. 2010 Biomimetic structures for fluid drag reduction in laminar and turbulent flows. J. Phys.: Condens. Matter 22, 035104.Google Scholar
Lamb, Sir H. 1916 Hydrodynamics, 4th edn, pp. 611–612. Cambridge University Press.Google Scholar
Lauga, E. & Stone, H. A. 2003 Effective slip in pressure-driven Stokes flow. J. Fluid Mech. 489, 55–77.Google Scholar
Martell, M. B., Perot, J. B. & Rothstein, J. P. 2009 Direct numerical simulations of turbulent flows over superhydrophobic surfaces. J. Fluid Mech. 620, 31–41.Google Scholar
Maynes, D., Jeffs, K., Woolford, B. & Webb, B. W. 2007 Laminar flow in a microchannel with hydrophobic surface patterned microribs oriented parallel to the flow direction. Phys. Fluids 19, 093603.Google Scholar
Min, T. & Kim, J. 2004 Effects of hydrophobic surface on skin-friction drag. Phys. Fluids 16, L55.Google Scholar
Park, H.2015 A numerical study of the effects of superhydrophobic surfaces on skin-friction drag reduction in wall-bounded shear flows. PhD thesis, University of California, Los Angeles.Google Scholar
Park, H., Park, H. & Kim, J. 2013 A numerical study of the effects of superhydrophobic surface on skin-friction drag in turbulent channel flow. Phys. Fluids 25, 110815.Google Scholar
Park, H., Sun, G. & Kim, C.-J. 2014 Superhydrophobic turbulent drag reduction as a function of surface grating parameters. J. Fluid Mech. 747, 722–734.CrossRefGoogle Scholar
Peguero, C. & Breuer, K. 2009 On drag reduction in turbulent channel flow over superhydrophobic surfaces. In Advance in Turbulence XII (ed. Eckhardt, B.), pp. 233–236. Springer.Google Scholar
Piao, L. & Park, H. 2015 Two-dimensional analysis of air–water interface on superhydrophobic grooves under fluctuating water pressure. Langmuir 31, 8022–8032.Google Scholar
Rastegari, A. & Akhavan, R. 2015 On the mechanism of turbulent drag reduction with super-hydrophobic surfaces. J. Fluid Mech. 773, R4.Google Scholar
Rothstein, J. P. 2010 Slip on superhydrophobic surfaces. Annu. Rev. Fluid Mech. 42, 89–109.Google Scholar
Seo, J., García-Mayoral, R. & Mani, A. 2015 Pressure fluctuations and interfacial robustness in turbulent flows over superhydrophobic surfaces. J. Fluid Mech. 783, 448–473.Google Scholar
Tretheway, D. C. & Meinhart, C. D. 2004 A generating mechanism for apparent fluid slip in hydrophobic microchannels. Phys. Fluids 16, 1509.Google Scholar
Türk, S., Daschiel, G., Stroh, A., Hasegawa, Y. & Frohnapfel, B. 2014 Turbulent flow over superhydrophobic surfaces with streamwise grooves. J. Fluid Mech. 747, 186–217.Google Scholar
Vinogradova, O. I. 1999 Slippage of water over hydrophobic surfaces. Intl J. Miner. Process. 56, 31–60.Google Scholar
Watanabe, K., Yanuar & Udagawa, H. 1999 Drag reduction of Newtonian fluid in a circular pipe with a highly water-repellent wall. J. Fluid Mech. 381, 225–238.Google Scholar
Woolford, B., Prince, J., Maynes, D. & Webb, B. W. 2009 Particle image velocimetry characterization of turbulent channel flow with rib patterned superhydrophobic walls. Phys. Fluids 21, 085106.Google Scholar
Zhao, J., Du, X. & Shi, X. 2007 Experimental research on friction-reduction with super-hydrophobic surfaces. J. Mar. Sci. Appl. 6, 58–61.Google Scholar