Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Wang, Dou
Lin, Qinfeng
Zhou, Chao
and
Wu, Jianghao
2022.
Aerodynamic performance of a self-propelled airfoil with a non-zero angle of attack.
Physics of Fluids,
Vol. 34,
Issue. 3,
Guo, Yueyang
Yang, Wenqing
Dong, Yuanbo
and
Xuan, Jianlin
2022.
Numerical investigation of an insect-scale flexible wing with a small amplitude flapping kinematics.
Physics of Fluids,
Vol. 34,
Issue. 8,
Addo-Akoto, Reynolds
Han, Jong-Seob
and
Han, Jae-Hung
2022.
Aerodynamic characteristics of flexible flapping wings depending on aspect ratio and slack angle.
Physics of Fluids,
Vol. 34,
Issue. 5,
Menzer, Alec
Ren, Yan
Guo, Jiacheng
Tobalske, Bret W.
and
Dong, Haibo
2022.
Wing Kinematics and Unsteady Aerodynamics of a Hummingbird Pure Yawing Maneuver.
Biomimetics,
Vol. 7,
Issue. 3,
p.
115.
Wu, Jianghao
Li, Gang
Chen, Long
and
Zhang, Yanlai
2022.
Unsteady aerodynamic performance of a tandem flapping–fixed airfoil configuration at low Reynolds number.
Physics of Fluids,
Vol. 34,
Issue. 11,
Noda, Ryusuke
Nakata, Toshiyuki
and
Liu, Hao
2023.
Effect of Hindwings on the Aerodynamics and Passive Dynamic Stability of a Hovering Hawkmoth.
Biomimetics,
Vol. 8,
Issue. 8,
p.
578.
Kang, Chang-kwon
Sridhar, Madhu
Twigg, Rachel
Pohly, Jeremy
Lee, Taeyoung
and
Aono, Hikaru
2023.
Power Benefits of High-Altitude Flapping Wing Flight at the Monarch Butterfly Scale.
Biomimetics,
Vol. 8,
Issue. 4,
p.
352.
Prapamonthon, Prasert
2023.
Hydrodynamic performance of a penguin wing: Effect of feathering and flapping.
Physics of Fluids,
Vol. 35,
Issue. 6,
Chen, Long
Zhang, Yanlai
Zhou, Chao
and
Wu, Jianghao
2023.
Vorticity dynamics of fully developed leading-edge vortices on revolving wings undergoing pitch-up maneuvers.
Physics of Fluids,
Vol. 35,
Issue. 3,
Chen, Long
Cheng, Bo
and
Wu, Jianghao
2023.
Vorticity dynamics and stability of the leading-edge vortex on revolving wings.
Physics of Fluids,
Vol. 35,
Issue. 9,
Meng, Xueguang
Liu, Xinyu
Chen, Zengshuang
Wu, Jianghao
and
Chen, Gang
2023.
Wing kinematics measurement and aerodynamics of hovering droneflies with wing damage.
Bioinspiration & Biomimetics,
Vol. 18,
Issue. 2,
p.
026013.
Paulson, James H.
Jardin, Thierry
and
Buchholz, James H. J.
2023.
Inflow-velocity and rotational effects on revolving and translating wings.
Physics of Fluids,
Vol. 35,
Issue. 11,
Chen, Long
Zhou, Chao
Werner, Nathaniel H.
Cheng, Bo
and
Wu, Jianghao
2023.
Dual-stage radial–tangential vortex tilting reverses radial vorticity and contributes to leading-edge vortex stability on revolving wings.
Journal of Fluid Mechanics,
Vol. 963,
Issue. ,
Wabick, Kevin J.
Johnson, Kyle C.
Berdon, Randall L.
Thurow, Brian S.
and
Buchholz, James H.J.
2023.
Transient leading-edge vortex development on a wing rolling in uniform flow.
Journal of Fluid Mechanics,
Vol. 957,
Issue. ,
Yu, Haocheng
Cui, Xinguang
Li, Guosheng
and
Zheng, Jianguo
2023.
Numerical Investigation of Flow Separation Control over Rotor Blades Using Plasma Actuator.
AIAA Journal,
Vol. 61,
Issue. 3,
p.
1151.
Chen, Long
and
Wu, Jianghao
2024.
Coexistence of dual wing–wake interaction mechanisms during the rapid rotation of flapping wings.
Journal of Fluid Mechanics,
Vol. 987,
Issue. ,
Li, Gang
Wu, Jianghao
Li, Jiaming
Zhang, Yanlai
and
Chen, Long
2024.
Trade-off of lifting and propulsion capacity of tandem flapping-fixed airfoils by inclining the stroke plane.
Acta Mechanica Sinica,
Vol. 40,
Issue. 5,
Chen, Zengshuang
Xie, Yuxin
Zhang, Yang
Li, Li
and
Meng, Xueguang
2024.
Aerodynamics of a flapping wing with stroke deviation in forward flight.
Physics of Fluids,
Vol. 36,
Issue. 5,
Yang, Xiaojun
Luo, Yang
Lang, Xinyu
and
Wang, Wei
2024.
Investigation of the aerodynamic performance of the dragonfly-inspired tandem wings considering the coupling between the stroke plane and phase difference.
Aerospace Science and Technology,
Vol. 155,
Issue. ,
p.
109717.
Addo-Akoto, Reynolds
Han, Jong-Seob
and
Han, Jae-Hung
2024.
Leading-edge curvature effect on aerodynamic performance of flapping wings in hover and forward flight.
Bioinspiration & Biomimetics,
Vol. 19,
Issue. 5,
p.
056007.
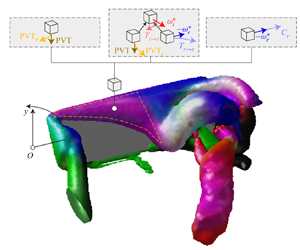
 $\textit {Re}$). In this study, using numerical methods, we examined the
$\textit {Re}$). In this study, using numerical methods, we examined the  $\textit {Re}$ dependence of LEV formation dynamics and stability on revolving wings with
$\textit {Re}$ dependence of LEV formation dynamics and stability on revolving wings with  $\textit {Re}$ ranging from 10 to 5000. Our results show that the duration of the LEV formation period and its steady-state intensity both reduce significantly as
$\textit {Re}$ ranging from 10 to 5000. Our results show that the duration of the LEV formation period and its steady-state intensity both reduce significantly as  $\textit {Re}$ decreases from 1000 to 10. Moreover, the primary mechanisms contributing to LEV stability can vary at different
$\textit {Re}$ decreases from 1000 to 10. Moreover, the primary mechanisms contributing to LEV stability can vary at different  $\textit {Re}$ levels. At
$\textit {Re}$ levels. At  $\textit {Re} <200$, the LEV stability is mainly driven by viscous diffusion. At
$\textit {Re} <200$, the LEV stability is mainly driven by viscous diffusion. At  $200<\textit {Re} <1000$, the LEV is maintained by two distinct vortex-tilting-based mechanisms, i.e. the planetary vorticity tilting and the radial–tangential vorticity balance. At
$200<\textit {Re} <1000$, the LEV is maintained by two distinct vortex-tilting-based mechanisms, i.e. the planetary vorticity tilting and the radial–tangential vorticity balance. At  $\textit {Re}>1000$, the radial–tangential vorticity balance becomes the primary contributor to LEV stability, in addition to secondary contributions from tip-ward vorticity convection, vortex compression and planetary vorticity tilting. It is further shown that the regions of tip-ward vorticity convection and tip-ward pressure gradient almost overlap at high
$\textit {Re}>1000$, the radial–tangential vorticity balance becomes the primary contributor to LEV stability, in addition to secondary contributions from tip-ward vorticity convection, vortex compression and planetary vorticity tilting. It is further shown that the regions of tip-ward vorticity convection and tip-ward pressure gradient almost overlap at high  $\textit {Re}$. In addition, the contribution of planetary vorticity tilting in LEV stability is
$\textit {Re}$. In addition, the contribution of planetary vorticity tilting in LEV stability is  $\textit {Re}$-independent. This work provides novel insights into the various mechanisms, in particular those of vortex tilting, in driving the LEV formation and stability on low-
$\textit {Re}$-independent. This work provides novel insights into the various mechanisms, in particular those of vortex tilting, in driving the LEV formation and stability on low- $\textit {Re}$ revolving wings.
$\textit {Re}$ revolving wings.