Article contents
Effects of Reynolds number and Stokes number on particle-pair relative velocity in isotropic turbulence: a systematic experimental study
Published online by Cambridge University Press: 26 January 2018
Abstract
The effects of Reynolds number (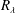 $R_{\unicode[STIX]{x1D706}}$) and Stokes number (
$R_{\unicode[STIX]{x1D706}}$) and Stokes number (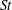 $St$) on particle-pair relative velocity (RV) are investigated systematically using a recently developed planar four-frame particle tracking technique in a novel homogeneous and isotropic turbulence chamber. We compare the measured results with direct numerical simulation (DNS), verifying whether the conclusions of the DNS for simplified conditions and limited
$St$) on particle-pair relative velocity (RV) are investigated systematically using a recently developed planar four-frame particle tracking technique in a novel homogeneous and isotropic turbulence chamber. We compare the measured results with direct numerical simulation (DNS), verifying whether the conclusions of the DNS for simplified conditions and limited 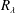 $R_{\unicode[STIX]{x1D706}}$ are still valid in reality. Two experiments are performed: varying
$R_{\unicode[STIX]{x1D706}}$ are still valid in reality. Two experiments are performed: varying 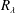 $R_{\unicode[STIX]{x1D706}}$ between 246 and 357 at six
$R_{\unicode[STIX]{x1D706}}$ between 246 and 357 at six 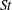 $St$ values, and varying
$St$ values, and varying 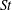 $St$ between 0.02 and 4.63 at five
$St$ between 0.02 and 4.63 at five 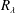 $R_{\unicode[STIX]{x1D706}}$ values. The measured mean inward particle-pair RV
$R_{\unicode[STIX]{x1D706}}$ values. The measured mean inward particle-pair RV 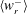 $\langle w_{r}^{-}\rangle$ as a function of separation distance
$\langle w_{r}^{-}\rangle$ as a function of separation distance  $r$ is compared with the DNS under closely matched conditions. At all experimental conditions, an excellent agreement is achieved, except when the particle separation distance
$r$ is compared with the DNS under closely matched conditions. At all experimental conditions, an excellent agreement is achieved, except when the particle separation distance 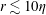 $r\lesssim 10\unicode[STIX]{x1D702}$ (
$r\lesssim 10\unicode[STIX]{x1D702}$ (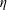 $\unicode[STIX]{x1D702}$ is the Kolmogorov length scale), where the experimental
$\unicode[STIX]{x1D702}$ is the Kolmogorov length scale), where the experimental 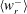 $\langle w_{r}^{-}\rangle$ is consistently higher, possibly due to particle polydispersity and finite laser thickness in the experiments (Dou et al., arXiv:1712.07506, 2017). At any fixed
$\langle w_{r}^{-}\rangle$ is consistently higher, possibly due to particle polydispersity and finite laser thickness in the experiments (Dou et al., arXiv:1712.07506, 2017). At any fixed 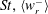 $St,\langle w_{r}^{-}\rangle$ is essentially independent of
$St,\langle w_{r}^{-}\rangle$ is essentially independent of 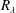 $R_{\unicode[STIX]{x1D706}}$, echoing the DNS finding of Ireland et al. (J. Fluid Mech., vol. 796, 2016, pp. 617–658). At any fixed
$R_{\unicode[STIX]{x1D706}}$, echoing the DNS finding of Ireland et al. (J. Fluid Mech., vol. 796, 2016, pp. 617–658). At any fixed 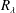 $R_{\unicode[STIX]{x1D706}}$,
$R_{\unicode[STIX]{x1D706}}$, 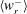 $\langle w_{r}^{-}\rangle$ increases with
$\langle w_{r}^{-}\rangle$ increases with 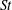 $St$ at small
$St$ at small  $r$, showing dominance of the path-history effect in the dissipation range when
$r$, showing dominance of the path-history effect in the dissipation range when 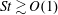 $St\gtrsim O(1)$, but decreases with
$St\gtrsim O(1)$, but decreases with 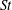 $St$ at large
$St$ at large  $r$, indicating dominance of inertial filtering. We further compare the
$r$, indicating dominance of inertial filtering. We further compare the 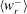 $\langle w_{r}^{-}\rangle$ and RV variance
$\langle w_{r}^{-}\rangle$ and RV variance 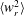 $\langle w_{r}^{2}\rangle$ from experiments with DNS and theoretical predictions by Pan & Padoan (J. Fluid Mech., vol. 661, 2010, pp. 73–107). For
$\langle w_{r}^{2}\rangle$ from experiments with DNS and theoretical predictions by Pan & Padoan (J. Fluid Mech., vol. 661, 2010, pp. 73–107). For 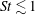 $St\lesssim 1$, experimental
$St\lesssim 1$, experimental 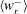 $\langle w_{r}^{-}\rangle$ and
$\langle w_{r}^{-}\rangle$ and 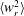 $\langle w_{r}^{2}\rangle$ match these values well at
$\langle w_{r}^{2}\rangle$ match these values well at 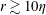 $r\gtrsim 10\unicode[STIX]{x1D702}$, but they are higher than both DNS and theory at
$r\gtrsim 10\unicode[STIX]{x1D702}$, but they are higher than both DNS and theory at 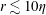 $r\lesssim 10\unicode[STIX]{x1D702}$. For
$r\lesssim 10\unicode[STIX]{x1D702}$. For 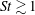 $St\gtrsim 1$,
$St\gtrsim 1$, 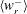 $\langle w_{r}^{-}\rangle$ from all three match well, except for
$\langle w_{r}^{-}\rangle$ from all three match well, except for 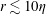 $r\lesssim 10\unicode[STIX]{x1D702}$, for which experimental values are higher, while
$r\lesssim 10\unicode[STIX]{x1D702}$, for which experimental values are higher, while 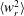 $\langle w_{r}^{2}\rangle$ from experiment and DNS are much higher than theoretical predictions. We discuss potential causes of these discrepancies. What this study shows is the first experimental validation of
$\langle w_{r}^{2}\rangle$ from experiment and DNS are much higher than theoretical predictions. We discuss potential causes of these discrepancies. What this study shows is the first experimental validation of 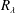 $R_{\unicode[STIX]{x1D706}}$ and
$R_{\unicode[STIX]{x1D706}}$ and 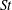 $St$ effect on inertial particle-pair
$St$ effect on inertial particle-pair 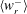 $\langle w_{r}^{-}\rangle$ in homogeneous and isotropic turbulence.
$\langle w_{r}^{-}\rangle$ in homogeneous and isotropic turbulence.
- Type
- JFM Papers
- Information
- Copyright
- © 2018 Cambridge University Press
Footnotes
Present address: 319 Latrobe Hall, Johns Hopkins University, Baltimore, MD 21218, USA
References
- 21
- Cited by


