Hostname: page-component-586b7cd67f-dsjbd Total loading time: 0 Render date: 2024-11-23T01:54:58.432Z Has data issue: false hasContentIssue false
  • English
  • Français

Effects of multi-scale and regular grid geometries on decaying turbulence

Published online by Cambridge University Press:  31 August 2016

R. Jason Hearst  and
Philippe Lavoie
R. Jason Hearst
Affiliation:
Institute for Aerospace Studies, University of Toronto, Toronto, ON M3H 5T6, Canada Engineering and the Environment, University of Southampton, Southampton SO17 1BJ, UK
Philippe Lavoie*
Affiliation:
Institute for Aerospace Studies, University of Toronto, Toronto, ON M3H 5T6, Canada
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

The influence of a multi-scale fractal based geometry on the decay of turbulence is investigated by comparing the turbulence produced by a square fractal element grid to that produced by two regular grids with similar physical properties. Comparison of the grid wakes at constant grid Reynolds number, 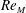$Re_{M}$, identifies that in the far field both regular grids produce comparable or higher turbulence intensities and local Reynolds numbers, 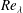$Re_{\unicode[STIX]{x1D706}}$, than the square fractal element grid. This result is illustrative of a limitation of multi-scale geometries to produce the oft-quoted high levels of turbulence intensity and 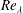$Re_{\unicode[STIX]{x1D706}}$. In the far field, the spectra are approximately collapsed at all scales for all three grids at a given 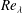$Re_{\unicode[STIX]{x1D706}}$. When a non-equilibrium near field spectrum with 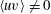$\langle uv\rangle \neq 0$ is compared to a far field spectrum at the same 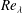$Re_{\unicode[STIX]{x1D706}}$ but with 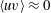$\langle uv\rangle \approx 0$, it is shown that their shapes are markedly different and that the non-equilibrium spectrum has a steeper slope, giving the appearance of being nearer 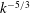$k^{-5/3}$, although there is no theoretical expectation of an inertial range at such locations in the flow. However, when a non-equilibrium spectrum with 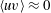$\langle uv\rangle \approx 0$ is compared to a far field spectrum at the same 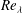$Re_{\unicode[STIX]{x1D706}}$, they are once again collapsed. This is shown to be related to non-zero Reynolds shear stress at scales that penetrate the scaling range for the present experiment, and hence the influence of shear is not limited to the largest scales. These results demonstrate the importance of local properties of the flow on the turbulence spectra at given locations in the inherently inhomogeneous flow found in the non-equilibrium region downstream of grids. In particular, how the presence of local shear stress can fundamentally change the shape of the spectra at scales that can be mistakenly interpreted as an inertial range.

JFM classification

Turbulent Flows: Homogeneous turbulence Turbulent Flows: Isotropic turbulence Turbulent Flows: Turbulent Flows
Type
Papers
Information
Journal of Fluid Mechanics , Volume 803 , 25 September 2016 , pp. 528 - 555
Check for updates
Copyright
© 2016 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Bailey, S. C. C., Kunkel, G. J., Hultmark, M., Vallikivi, M., Hill, J. P., Meyer, K. A., Tsay, C., Arnold, C. B. & Smits, A. J. 2010 Turbulence measurements using a nanoscale thermal anemometry probe. J. Fluid Mech. 663, 160–179.Google Scholar
Bell, J. H. & Mehta, R. D.1988 Contraction design for small low-speed wind tunnels NASA Contractor Rep. 177488.Google Scholar
Benedict, L. H. & Gould, R. D. 1996 Towards better uncertainty estimates for turbulence statistics. Exp. Fluids 22, 129–136.CrossRefGoogle Scholar
Burattini, P. & Antonia, R. A. 2005 The effect of different X-wire calibration schemes on some turbulence statistics. Exp. Fluids 38, 80–89.Google Scholar
Cafiero, G., Discetti, S. & Astarita, T. 2015 Flow field topology of submerged jets with fractal generated turbulence. Phys. Fluids 27, 115103.CrossRefGoogle Scholar
Castro, I. P. 2016 Dissipative distinctions. J. Fluid Mech. 788, 1–4.Google Scholar
Comte-Bellot, G. & Corrsin, S. 1966 The use of a contraction to improve the isotropy of grid-generated turbulence. J. Fluid Mech. 25 (4), 657–682.Google Scholar
Dairay, T., Obligado, M. & Vassilicos, J. C. 2015 Non-equilibrium scaling laws in axisymmetric turbulent wakes. J. Fluid Mech. 781, 166–195.Google Scholar
Frisch, U. 1995 Turbulent Flows. Cambridge University Press.Google Scholar
Geipel, P., Goh, K. H. H. & Lindstedt, R. P. 2010 Fractal-generated turbulence in opposed jet flows. Flow Turbul. Combust. 85, 397–419.Google Scholar
Hearst, R. J., Buxton, O. R. H., Ganapathisubramani, B. & Lavoie, P. 2012 Experimental estimation of fluctuating velocity and scalar gradients in turbulence. Exp. Fluids 53 (4), 925–942.Google Scholar
Hearst, R. J. & Lavoie, P. 2014a Decay of turbulence generated by a square-fractal-element grid. J. Fluid Mech. 741, 567–584.Google Scholar
Hearst, R. J. & Lavoie, P. 2014b Scale-by-scale energy budget in fractal element grid-generated turbulence. J. Turbul. 15 (8), 540–554.Google Scholar
Hearst, R. J. & Lavoie, P. 2015a The effect of active grid initial conditions on high Reynolds number turbulence. Exp. Fluids 56 (10), 185.CrossRefGoogle Scholar
Hearst, R. J. & Lavoie, P. 2015b Velocity derivative skewness in fractal-generated, non-equilibrium grid turbulence. Phys. Fluids 27 (7), 071701.Google Scholar
Hurst, D. & Vassilicos, J. C. 2007 Scalings and decay of fractal-generated turbulence. Phys. Fluids 19, 035103.Google Scholar
Isaza, J. C., Salazar, R. & Warhaft, Z. 2014 On grid-generated turbulence in the near- and far field regions. J. Fluid Mech. 753, 402–426.Google Scholar
Jørgensen, F. E. 2002 How to Measure Turbulence With Hot-Wire Anemometers – A Practical Guide. Dantec Dynamics.Google Scholar
Kinzel, M., Wolf, M., Holzner, M., Lüthi, B., Tropea, C. & Kinzelbach, W. 2011 Simultaneous two-scale 3D-PTV measurements in turbulence under the influence of system rotation. Exp. Fluids 51, 75–82.Google Scholar
Kolmogorov, A. N. 1941 On the degeneration of isotropic turbulence in an incompressible viscous fluid. Dokl. Akad. Nauk SSSR 31, 538–541.Google Scholar
Kolmogorov, A. N. 1962 A refinement of previous hypotheses concerning the local structure of turbulence in a viscous incompressible fluid at high Reynolds number. J. Fluid Mech. 13, 82–85.Google Scholar
Krogstad, P.-A. & Davidson, P. A. 2010 Is grid turbulence Saffman turbulence? J. Fluid Mech. 642, 373–394.Google Scholar
Krogstad, P.-A. & Davidson, P. A. 2011 Freely decaying, homogeneous turbulence generated by multi-scale grids. J. Fluid Mech. 680, 417–434.Google Scholar
Krogstad, P.-A. & Davidson, P. A. 2012 Near-field investigation of turbulence produced by multi-scale grids. Phys. Fluids 24, 035103.Google Scholar
Laizet, S., Nedić, J. & Vassilicos, J. C. 2015 The spatial origin of - 5/3 spectra in grid-generated turbulence. Phys. Fluids 27, 065115.Google Scholar
Laizet, S. & Vassilicos, J. C. 2015 Stirring and scalar transfer by grid-generated turbulence in the presence of a mean scalar gradient. J. Fluid Mech. 764, 52–75.Google Scholar
Lavoie, P., Djenidi, L. & Antonia, R. A. 2007 Effects of initial conditions in decaying turbulence generated by passive grids. J. Fluid Mech. 585, 395–420.Google Scholar
Lumley, J. L. 1992 Some comments on turbulence. Phys. Fluids A 4 (2), 203–211.Google Scholar
Mazellier, N. & Vassilicos, J. C. 2010 Turbulence without Richardson–Kolmogorov cascade. Phys. Fluids 22, 075101.CrossRefGoogle Scholar
Mi, J. & Antonia, R. A. 2001 Effect of large-scale intermittency and mean shear on scaling-range exponents in a turbulent jet. Phys. Rev. E 64, 026302.Google Scholar
Mi, J., Deo, R. C. & Nathan, G. J. 2005 Fast-convergence iterative scheme for filtering velocity signals and finding Kolmogorov scales. Phys. Rev. E 71, 066304.Google Scholar
Mohamed, M. S. & LaRue, J. C. 1990 The decay power law in grid-generated turbulence. J. Fluid Mech. 219, 195–214.Google Scholar
Mydlarski, L. & Warhaft, Z. 1996 On the onset of high-Reynolds-number grid-generated wind tunnel turbulence. J. Fluid Mech. 320, 331–368.Google Scholar
Nagata, K., Sakai, Y., Inaba, T., Suzuki, H., Terashima, O. & Suzuki, H. 2013 Turbulence structure and turbulence kinetic energy transport in multiscale/fractal-generated turbulence. Phys. Fluids 25, 065102.Google Scholar
Nedić, J., Ganapathisubramani, B., Vassilicos, J. C., Borée, J., Brizzi, L. E. & Spohn, A. 2012 Aeroacoustic performance of fractal spoilers. AIAA J. 50 (12), 2695–2710.Google Scholar
Nedić, J., Vassilicos, J. C. & Ganapathisubramani, B. 2013 Axisymmetric turbulent wakes with new nonequilibrium similarity scalings. Phys. Rev. Lett. 111, 144503.Google Scholar
Saddoughi, S. G. & Veeravalli, S. V. 1994 Local isotropy in turbulent boundary layers at high Reynolds number. J. Fluid Mech. 268, 333–372.Google Scholar
Seoud, R. E. & Vassilicos, J. C. 2007 Dissipation and decay of fractal-generated turbulence. Phys. Fluids 19, 105108.Google Scholar
Sinhuber, M., Bodenschatz, E. & Bewley, G. P. 2015 Decay of turbulence at high Reynolds numbers. Phys. Rev. Lett. 114, 034501.Google Scholar
Soulopoulus, N., Kerl, J., Sponfeldner, T., Beyrau, F., Hardalupas, Y., Taylor, A. M. K. P. & Vassilicos, J. C. 2013 Turbulent premixed flames on fractal-grid-generated turbulence. Fluid Dyn. Res. 45 (6), 061404.Google Scholar
Thormann, A. & Meneveau, C. 2014 Decay of homogeneous, nearly isotropic turbulence behind active fractal grids. Phys. Fluids 26, 025112.Google Scholar
Valente, P. C. & Vassilicos, J. C. 2011 The decay of turbulence generated by a class of multiscale grids. J. Fluid Mech. 687, 300–340.Google Scholar
Valente, P. C. & Vassilicos, J. C. 2012 Universal dissipation scaling for nonequilibrium turbulence. Phys. Rev. Lett. 108, 214503.Google Scholar
Valente, P. C. & Vassilicos, J. C. 2014 The non-equilibrium region of grid-generated decaying turbulence. J. Fluid Mech. 744, 5–37.Google Scholar
Vallikivi, M., Hultmark, M., Bailey, S. C. C. & Smits, A. J. 2011 Turbulence measurements in pipe flow using a nano-scale thermal anemometry probe. Exp. Fluids 51, 1521–1527.Google Scholar
Vassilicos, J. C. 2015 Dissipation in turbulent flows. Annu. Rev. Fluid Mech. 47, 95–114.Google Scholar
Verbeek, A. A., Bouten, T. W. F. M., Stoffels, G. G. M., Geurts, B. J. & van der Meer, T. H. 2015 Fractal turbulence enhancing low-swirl combustion. Combust. Flame 162, 129–143.Google Scholar
Wang, H. & George, W. K. 2002 The integral scale in homogeneous isotropic turbulence. J. Fluid Mech. 459, 429–443.Google Scholar
Weitemeyer, S., Reinke, N., Peinke, J. & Hölling, M. 2013 Multi-scale generation of turbulence with fractal grids and an active grid. Fluid Dyn. Res. 45 (6), 061407.Google Scholar
Wyngaard, J. C. 1968 Measurements of small-scale turbulence structure with hot wires. J. Sci. Instrum. 1 (2), 1105–1108.Google Scholar
Zhou, Y., Nagata, K., Sakai, Y., Suzuki, H., Ito, Y., Terashima, O. & Hayase, T. 2014 Relevance of turbulence behind the single square grid to turbulence generated by regular- and multiscale-grids. Phys. Fluids 26, 075105.Google Scholar