Article contents
Effects of mean shear on the local turbulent entrainment process
Published online by Cambridge University Press: 14 August 2013
Abstract
We report on effects of mean shear on the turbulent entrainment process, focusing in particular on their relation to small-scale processes in the proximity of the turbulent/non-turbulent interface (TNTI). Three-dimensional particle tracking velocimetry (3D-PTV) measurements of an axisymmetric jet are compared to data from a direct numerical simulation (DNS) of a zero-mean-shear (ZMS) flow. First, conditional statistics relative to the interface position are investigated in a pseudo-Eulerian view (i.e. in a fixed frame relative to the interface position) and in a Lagrangian view. We find that in a pseudo-Eulerian frame of reference, both vorticity fluctuations and mean shear contribute to the vorticity jump at the boundary between irrotational and turbulent regions. In contrast, the Lagrangian evolution of enstrophy along trajectories crossing the entrainment interface is almost exclusively dominated by vorticity fluctuations, at least during the first Kolmogorov time scales after passing the interface. A mapping between distance to the instantaneous interface versus conditional time along the trajectory shows that entraining particles remain initially close to the TNTI and therefore attain lower average enstrophy values. The ratio between the rate of change of enstrophy in the two frames of references defines the local entrainment velocity 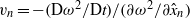 ${v}_{n} = - (\mathrm{D} {\omega }^{2} / \mathrm{D} t)/ (\partial {\omega }^{2} / \partial {\hat {x} }_{n} )$, where
${v}_{n} = - (\mathrm{D} {\omega }^{2} / \mathrm{D} t)/ (\partial {\omega }^{2} / \partial {\hat {x} }_{n} )$, where 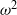 ${\omega }^{2} $ is enstrophy and
${\omega }^{2} $ is enstrophy and 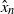 ${\hat {x} }_{n} $ is the coordinate normal to the TNTI. The quantity
${\hat {x} }_{n} $ is the coordinate normal to the TNTI. The quantity 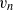 ${v}_{n} $ is decomposed into mean and fluctuating components and it is found that mean shear enhances the local entrainment velocity via inviscid and viscous effects. Further, the analysis substantiates that for all investigated flow configurations the local entrainment velocity depends considerably on the geometrical shape of the interface. Depending on the surface shape, different small-scale mechanisms are dominant for the local entrainment process, i.e. viscous effects for convex shapes and vortex stretching for concave shapes, looking from the turbulent region towards the convoluted boundary. Moreover, turbulent fluctuations display a stronger dependence on the shape of the interface than mean shear effects.
${v}_{n} $ is decomposed into mean and fluctuating components and it is found that mean shear enhances the local entrainment velocity via inviscid and viscous effects. Further, the analysis substantiates that for all investigated flow configurations the local entrainment velocity depends considerably on the geometrical shape of the interface. Depending on the surface shape, different small-scale mechanisms are dominant for the local entrainment process, i.e. viscous effects for convex shapes and vortex stretching for concave shapes, looking from the turbulent region towards the convoluted boundary. Moreover, turbulent fluctuations display a stronger dependence on the shape of the interface than mean shear effects.
JFM classification
- Type
- Papers
- Information
- Copyright
- ©2013 Cambridge University Press
References
- 43
- Cited by


