Published online by Cambridge University Press: 13 December 2016
For low-Reynolds-number shear flows of neutrally buoyant suspensions, the shear stress is often modelled using an effective viscosity that depends only on the solid fraction. As the Reynolds number (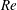 $Re$) is increased and inertia becomes important, the effective viscosity also depends on the Reynolds number itself. The current experiments measure the torque for flows of neutrally buoyant particles in a coaxial-cylinder rheometer for solid fractions,
$Re$) is increased and inertia becomes important, the effective viscosity also depends on the Reynolds number itself. The current experiments measure the torque for flows of neutrally buoyant particles in a coaxial-cylinder rheometer for solid fractions, 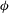 $\unicode[STIX]{x1D719}$, from 10 % to 50 % and Reynolds numbers based on particle diameter from 2 to 1000. For experiments for Reynolds of
$\unicode[STIX]{x1D719}$, from 10 % to 50 % and Reynolds numbers based on particle diameter from 2 to 1000. For experiments for Reynolds of 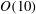 $O(10)$ and solid fractions less than
$O(10)$ and solid fractions less than 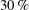 $30\,\%$, the effective viscosity increases with Reynolds number, in good agreement with recent numerical simulations found in the literature. At higher solid fractions over the same range of
$30\,\%$, the effective viscosity increases with Reynolds number, in good agreement with recent numerical simulations found in the literature. At higher solid fractions over the same range of  $Re$, the results show a decrease in torque with shear rate. For Reynolds numbers greater than 100 and lower solids concentrations, the effective viscosity continues to increase with Reynolds number. However, based on comparisons with pure fluid measurements the increase in the measured effective viscosity results from the transition to turbulence. The particles augment the turbulence by increasing the magnitude of the measured torques and causing the flow to transition at lower Reynolds numbers. For the highest solid fractions, the measurements show a significant increase in the magnitude of the torques, but the effective viscosity is independent of Reynolds number.
$Re$, the results show a decrease in torque with shear rate. For Reynolds numbers greater than 100 and lower solids concentrations, the effective viscosity continues to increase with Reynolds number. However, based on comparisons with pure fluid measurements the increase in the measured effective viscosity results from the transition to turbulence. The particles augment the turbulence by increasing the magnitude of the measured torques and causing the flow to transition at lower Reynolds numbers. For the highest solid fractions, the measurements show a significant increase in the magnitude of the torques, but the effective viscosity is independent of Reynolds number.