Hostname: page-component-586b7cd67f-rdxmf Total loading time: 0 Render date: 2024-11-30T19:14:39.889Z Has data issue: false hasContentIssue false
  • English
  • Français

Effects of frontal and plan solidities on aerodynamic parameters and the roughness sublayer in turbulent boundary layers

Published online by Cambridge University Press:  09 October 2015

M. Placidi  and
B. Ganapathisubramani
M. Placidi
Affiliation:
Aerodynamics and Flight Mechanics Research Group, Faculty of Engineering and the Environment, University of Southampton, Southampton SO17 1BJ, UK
B. Ganapathisubramani*
Affiliation:
Aerodynamics and Flight Mechanics Research Group, Faculty of Engineering and the Environment, University of Southampton, Southampton SO17 1BJ, UK
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

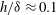Experiments were conducted in the fully rough regime on surfaces with large relative roughness height ($h/{\it\delta}\approx 0.1$, where 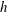$h$ is the roughness height and 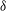${\it\delta}$ is the boundary layer thickness). The surfaces were generated by distributed LEGO® bricks of uniform height, arranged in different configurations. Measurements were made with both floating-element drag balance and high-resolution particle image velocimetry on six configurations with different frontal solidities, 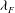${\it\lambda}_{F}$, at fixed plan solidity, 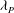${\it\lambda}_{P}$, and vice versa, for a total of twelve rough-wall cases. The results indicated that the drag reaches a peak value 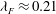${\it\lambda}_{F}\approx 0.21$ for a constant 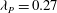${\it\lambda}_{P}=0.27$, while it monotonically decreases for increasing values of 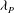${\it\lambda}_{P}$ for a fixed 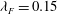${\it\lambda}_{F}=0.15$. This is in contrast to previous studies in the literature based on cube roughness which show a peak in drag for both 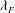${\it\lambda}_{F}$ and 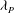${\it\lambda}_{P}$ variations. The influence of surface morphology on the depth of the roughness sublayer (RSL) was also investigated. Its depth was found to be inversely proportional to the roughness length, 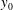$y_{0}$. A decrease in 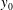$y_{0}$ was usually accompanied by a thickening of the RSL and vice versa. Proper orthogonal decomposition (POD) analysis was also employed. The shapes of the most energetic modes calculated using the data across the entire boundary layer were found to be self-similar across the twelve rough-wall cases. However, when the analysis was restricted to the roughness sublayer, differences that depended on the wall morphology were apparent. Moreover, the energy content of the POD modes within the RSL suggested that the effect of increased frontal solidity was to redistribute the energy towards the larger scales (i.e. a larger portion of the energy was within the first few modes), while the opposite was found for variation of plan solidity.

JFM classification

Boundary Layers: Boundary layer structure Turbulent Flows: Turbulent boundary layers
Type
Papers
Information
Journal of Fluid Mechanics , Volume 782 , 10 November 2015 , pp. 541 - 566
Check for updates
Copyright
© 2015 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Acharya, M., Bornstein, J. & Escudier, M. P. 1986 Turbulent boundary layers on rough surfaces. Exp. Fluids 4, 33–47.CrossRefGoogle Scholar
Adrian, R. J., Christensen, K. T. & Liu, Z. C. 2000 Analysis and interpretation of instantaneous turbulent velocity fields. Exp. Fluids 29, 275–290.CrossRefGoogle Scholar
Adrian, R. J. & Westerweel, J. 2011 Particle Image Velocimetry. Cambridge University Press.Google Scholar
Amir, M. & Castro, I. P. 2011 Turbulence in rough-wall boundary layers: universality issues. Exp. Fluids 51, 313–326.CrossRefGoogle Scholar
Barros, J. M. & Christensen, K. T. 2014 Observations of turbulent secondary flows in a rough-wall boundary layer. J. Fluid Mech. 748, R1.CrossRefGoogle Scholar
Benedict, L. H. & Gould, R. D. 1996 Towards better uncertainty estimates for turbulence statistics. Exp. Fluids 22, 129–136.CrossRefGoogle Scholar
Berkooz, G., Holmes, P. & Lumley, J. L. 1993 The proper orthogonal decomposition in the analysis of turbulent flows. Annu. Rev. Fluid Mech. 25, 539–575.CrossRefGoogle Scholar
Castro, I. P. 2007 Rough-wall boundary layers: mean flow universality. J. Fluid Mech. 585, 469–485.CrossRefGoogle Scholar
Castro, I. P., Segalini, A. & Alfredsson, P. H. 2013 Outer-layer turbulence intensities in smooth- and rough-wall boundary layers. J. Fluid Mech. 727, 119–131.CrossRefGoogle Scholar
Cheng, H. & Castro, I. P. 2002a Near-wall flow development after a step change in surface roughness. Boundary-Layer Meteorol. 105, 411–432.CrossRefGoogle Scholar
Cheng, H. & Castro, I. P. 2002b Near wall flow over urban-like roughness. Boundary-Layer Meteorol. 105, 411–432.CrossRefGoogle Scholar
Cheng, H., Hayden, P., Robins, A. G. & Castro, I. P. 2007 Flow over cube arrays of different packing densities. J. Wind Engng Ind. Aerodyn. 95 (8), 715–740.CrossRefGoogle Scholar
Coceal, O. & Belcher, S. E. 2004 A canopy model of mean winds through urban areas. Q. J. R. Meteorol. Soc. 130 (599), 1349–1372.CrossRefGoogle Scholar
Efros, V.2011 Structure of turbulent boundary layer over a 2-D roughness. PhD thesis, Norwegian University of Science and Technology.Google Scholar
Flack, K. A., Schultz, M. P. & Connelly, J. S. 2007 Examination of a critical roughness height for outer layer similarity. Phys. Fluids 19 (9), 095104.CrossRefGoogle Scholar
Flack, K. A., Schultz, M. P. & Shapiro, T. A. 2005 Experimental support for Townsend’s Reynolds number similarity hypothesis on rough walls. Phys. Fluids 17 (3), 035102.CrossRefGoogle Scholar
Grimmond, C. S. B. & Oke, T. R. 1999 Aerodynamic properties of urban areas derived, from analysis of surface form. J. Appl. Meteorol. 38, 1262–1292.2.0.CO;2>CrossRefGoogle Scholar
Hagishima, A., Tanimoto, J., Nagayama, K. & Meno, S. 2009 Aerodynamic parameters of regular arrays of rectangular blocks with various geometries. Boundary-Layer Meteorol. 132, 315–337.CrossRefGoogle Scholar
Iyengar, A. K. S. & Farell, C. 2001 Experimental issues in atmospheric boundary layer simulations: roughness length and integral length scale determination. J. Wind Engng Ind. Aerodyn. 89, 1059–1080.CrossRefGoogle Scholar
Jackson, P. S. 1976 The propagation of modified flow downstream of a change in roughness. Q. J. R. Meteorol. Soc. 102, 924–933.Google Scholar
Jackson, P. S. 1981 On the displacement height in the logarithmic velocity profile. J. Fluid Mech. 111, 15–25.CrossRefGoogle Scholar
Jimenez, J. 2004 Turbulent flows over rough walls. Annu. Rev. Fluid Mech. 36, 173–196.CrossRefGoogle Scholar
Kanda, M., Inagaki, A., Miyamoto, T., Gryschka, M. & Raasch, S. 2013 A new aerodynamic parametrization for real urban surfaces. Boundary-Layer Meteorol. 148 (2), 357–377.CrossRefGoogle Scholar
Kanda, M., Moriwaki, R. & Kasamatsu, F. 2004 Large-eddy simulation of turbulent organized structures within and above explicitly resolved cube arrays. Boundary-Layer Meteorol. 112 (2), 343–368.CrossRefGoogle Scholar
Krogstad, P. A. & Efros, V. 2010 Rough wall skin friction measurements using a high resolution surface balance. Intl J. Heat Fluid Flow 31 (3), 429–433.CrossRefGoogle Scholar
Leonardi, S. & Castro, I. P. 2010 Channel flow over large cube roughness: a direct numerical simulation study. J. Fluid Mech. 651, 519–539.CrossRefGoogle Scholar
Leonardi, S., Orlandi, P., Smalley, R. J., Djenidi, L. & Antonia, R. A. 2003 Direct numerical simulations of turbulent channel flow with transverse square bars on one wall. J. Fluid Mech. 491, 229–238.CrossRefGoogle Scholar
Macdonald, R. W. 1998 An improved method for the estimation of surface roughness of obstacle arrays. Boundary-Layer Meteorol. 97, 1857–1864.Google Scholar
Manes, C., Poggi, D. & Ridolfi, L. 2011 Turbulent boundary layers over permeable walls: scaling and near-wall structure. J. Fluid Mech. 687, 141–170.CrossRefGoogle Scholar
Marusic, I., Monty, J. P., Hultmark, M. & Smits, A. J. 2013 On the logarithmic region in wall turbulence. J. Fluid Mech. 716, R3, 1–11.CrossRefGoogle Scholar
Mejia-Alvarez, R. & Christensen, K. T. 2013 Wall-parallel stereo particle-image velocimetry measurements in the roughness sublayer of turbulent flow overlying highly irregular roughness. Phys. Fluids 25 (11), 115109.Google Scholar
Millward-Hopkins, J. T., Tomlin, A. S., Ma, L., Ingham, D. & Pourkashanian, M. 2011 Estimating aerodynamic parameters of urban-like surfaces with heterogeneous building heights. Boundary-Layer Meteorol. 141 (3), 467–490.CrossRefGoogle Scholar
Nikuradse, J.1933 Laws of flow in rough pipes. NACA Tech. Mem. 1292.Google Scholar
Pearson, D. S., Goulart, P. J. & Ganapathisubramani, B. 2013 Turbulent separation upstream of a forward-facing step. J. Fluid Mech. 724, 284–304.CrossRefGoogle Scholar
Raffel, M., Willert, C. & Kompenhans, J. 1998 Particle Image Velocimetry, 2nd edn. Springer.CrossRefGoogle Scholar
Raupach, M. R., Antonia, R. A. & Rajagopalan, S. 1991 Rough-wall turbulent boundary layers. Appl. Mech. Rev. 44 (1), 1–25.CrossRefGoogle Scholar
Reynolds, R. T. & Castro, I. P. 2008 Measurements in an urban-type boundary layer. Exp. Fluids 45, 141–156.CrossRefGoogle Scholar
Reynolds, R. T., Hayden, P., Castro, I. P. & Robins, A. G. 2007 Spanwise variations in nominally two-dimensional rough-wall boundary layers. Exp. Fluids 42, 311–320.CrossRefGoogle Scholar
Santiago, J. L., Coceal, O., Martilli, A. & Belcher, S. E. 2008 Variation of the sectional drag coefficient of a group of buildings with packing density. Boundary-Layer Meteorol. 128, 445–457.CrossRefGoogle Scholar
Schlichting, H. 1937 Experimental investigation of the problem of surface roughness. NACA Tech. Mem. 823, 1–60.Google Scholar
Schultz, M. P. & Flack, K. A. 2005 Outer layer similarity in fully rough turbulent boundary layers. Exp. Fluids 38 (3), 328–340.CrossRefGoogle Scholar
Segalini, A., Örlü, R. & Alfredsson, P. H. 2013 Uncertainty analysis of the von Kármán constant. Exp. Fluids 54, 1460.CrossRefGoogle Scholar
Wu, Y. & Christensen, K. T. 2007 Outer-layer similarity in the presence of a practical rough-wall topography. Phys. Fluids 19 (8), 085108.CrossRefGoogle Scholar