Hostname: page-component-586b7cd67f-r5fsc Total loading time: 0 Render date: 2024-11-22T23:55:08.811Z Has data issue: false hasContentIssue false
  • English
  • Français

Effects of flapping-motion profiles on insect-wing aerodynamics

Published online by Cambridge University Press:  03 December 2019

Shantanu S. Bhat Open the ORCID record for Shantanu S. Bhat [Opens in a new window] ,
Jisheng Zhao ,
John Sheridan Open the ORCID record for John Sheridan [Opens in a new window] ,
Kerry Hourigan  and
Mark C. Thompson
Shantanu S. Bhat*
Affiliation:
Fluids Laboratory for Aeronautical and Industrial Research (FLAIR), Department of Mechanical and Aerospace Engineering, Monash University, Melbourne, VIC 3800, Australia
Jisheng Zhao
Affiliation:
Fluids Laboratory for Aeronautical and Industrial Research (FLAIR), Department of Mechanical and Aerospace Engineering, Monash University, Melbourne, VIC 3800, Australia
John Sheridan
Affiliation:
Fluids Laboratory for Aeronautical and Industrial Research (FLAIR), Department of Mechanical and Aerospace Engineering, Monash University, Melbourne, VIC 3800, Australia
Kerry Hourigan
Affiliation:
Fluids Laboratory for Aeronautical and Industrial Research (FLAIR), Department of Mechanical and Aerospace Engineering, Monash University, Melbourne, VIC 3800, Australia
Mark C. Thompson
Affiliation:
Fluids Laboratory for Aeronautical and Industrial Research (FLAIR), Department of Mechanical and Aerospace Engineering, Monash University, Melbourne, VIC 3800, Australia
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Flapping wings of insects can follow various complex-motion waveforms, influencing the flow structures over a wing and consequently the aerodynamic performance. However, most studies of insect-wing models incorporate either simple harmonic or robofly-like motion waveforms. The effects of other waveforms appear to be under-explored. Motivated by this, the present study investigates the individual and combined effects of the sweep- and pitch-motion waveforms for fixed flapping frequency and amplitude of a fruit-fly wing planform. Physical experiments are conducted to directly measure the forces and torques acting on the wing. Interestingly, the sweep waveform is observed to influence the overall variation in the lift coefficient ($C_{L}$), whereas the pitch waveform is observed to influence only the instantaneous $C_{L}$ during stroke reversal. Carefully validated three-dimensional numerical simulations reveal that a change in the strength of the large-scale vortex over the wing as the sweep profile parameter is varied is responsible for the observed variations in $C_{L}$. An exploration over wide ranges of the sweep and the pitch profile parameters shows that the waveforms maximising the mean lift coefficient are different from those maximising the power economy. Consistent with some previous experiments on robotic insects, the possibility of passive pitch motion is observed at slower pitching rates. Contours of the mean lift coefficient and power economy mapped on the planes of the sweep and the pitch profile parameters can help designers of flapping-wing micro air vehicles in selecting the waveforms appropriate for their design criteria.

JFM classification

Biological Fluid Dynamics: Swimming/flying
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 884 , 10 February 2020 , A8
Copyright
© 2019 Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Altshuler, D. L., Dickson, W. B., Vance, J. T., Roberts, S. P. & Dickinson, M. H. 2005 Short-amplitude high-frequency wing strokes determine the aerodynamics of honeybee flight. Proc. Natl Acad. Sci. USA 102 (50), 18213–18218.CrossRefGoogle ScholarPubMed
Ansari, S. A., Knowles, K. & Zbikowski, R. 2008 Insectlike flapping wings in the hover. Part I: effect of wing kinematics. J. Aircraft 45 (6), 1945–1954.CrossRefGoogle Scholar
Bergou, A. J., Xu, S. & Wang, Z. J. 2007 Passive wing pitch reversal in insect flight. J. Fluid Mech. 591, 321–337.CrossRefGoogle Scholar
Berman, G. J. & Wang, Z. J. 2007 Energy-minimizing kinematics in hovering insect flight. J. Fluid Mech. 582, 153–168.CrossRefGoogle Scholar
Bhat, S. S., Zhao, J., Sheridan, J., Hourigan, K. & Thompson, M. C. 2019 Uncoupling the effects of aspect ratio, Reynolds number and Rossby number on a rotating insect-wing planform. J. Fluid Mech. 859, 921–948.CrossRefGoogle Scholar
Birch, J. M. & Dickinson, M. H. 2003 The influence of wing-wake interactions on the production of aerodynamic forces in flapping flight. J. Expl Biol. 206 (13), 2257–2272.CrossRefGoogle ScholarPubMed
Bluman, J. & Kang, C.-K. 2017 Wing–wake interaction destabilizes hover equilibrium of a flapping insect-scale wing. Bioinspir. Biomim. 12 (4), 046004.CrossRefGoogle ScholarPubMed
Bos, F. M., Lentink, D., Van Oudheusden, B. W. & Bijl, H. 2008 Influence of wing kinematics on performance in hovering insect flight. J. Fluid Mech. 594, 341–368.CrossRefGoogle Scholar
Chen, Y. H. & Skote, M. 2016 Gliding performance of 3-D corrugated dragonfly wing with spanwise variation. J. Fluids Struct. 62, 1–13.CrossRefGoogle Scholar
Dickinson, M. H., Lehmann, F.-O. & Sane, S. P. 1999 Wing rotation and the aerodynamic basis of insect flight. Science 284 (5422), 1954–1960.CrossRefGoogle ScholarPubMed
Ellington, C. P. 1984 The aerodynamics of hovering insect flight. III. Kinematics. Phil. Trans. R. Soc. Lond. B 305 (1122), 41–78.CrossRefGoogle Scholar
Ellington, C. P., van den Berg, C., Willmott, A. P. & Thomas, A. L. R. 1996 Leading-edge vortices in insect flight. Nature 384 (6610), 626–630.CrossRefGoogle Scholar
Ennos, A. R. 1988 The importance of torsion in the design of insect wings. J. Expl Biol. 140 (1), 137–160.Google Scholar
Fry, S. N., Sayaman, R. & Dickinson, M. H. 2005 The aerodynamics of hovering flight in Drosophila. J. Expl Biol. 208 (12), 2303–2318.CrossRefGoogle ScholarPubMed
Garmann, D. J. & Visbal, M. R. 2013 A numerical study of hovering wings undergoing revolving or translating motions. In 31st AIAA Applied Aerodynamics Conference, Reston, Virginia, AIAA Paper 2013-3052.Google Scholar
Ghommem, M., Hajj, M. R., Mook, D. T., Stanford, B. K., Beran, P. S. & Watson, L. T. 2013 Global-local optimization of flapping kinematics in hovering flight. Intl J. Micro Air Veh. 5 (2), 4–7.Google Scholar
Harbig, R. R., Sheridan, J. & Thompson, M. C. 2013 Reynolds number and aspect ratio effects on the leading-edge vortex for rotating insect wing planforms. J. Fluid Mech. 717, 166–192.CrossRefGoogle Scholar
Harbig, R. R., Sheridan, J. & Thompson, M. C. 2014 The role of advance ratio and aspect ratio in determining leading-edge vortex stability for flapping flight. J. Fluid Mech. 751, 71–105.CrossRefGoogle Scholar
Izraelevitz, J. S. & Triantafyllou, M. S. 2014 Adding in-line motion and model-based optimization offers exceptional force control authority in flapping foils. J. Fluid Mech. 742, 5–34.CrossRefGoogle Scholar
Jones, M. A. 2003 The separated flow of an inviscid fluid around a moving flat plate. J. Fluid Mech. 496, 405–441.CrossRefGoogle Scholar
Khan, Z. A. & Agrawal, S. K. 2011 Optimal hovering kinematics of flapping wings for micro air vehicles. AIAA J. 49 (2), 257–268.CrossRefGoogle Scholar
Lentink, D. & Dickinson, M. H. 2009 Rotational accelerations stabilize leading edge vortices on revolving fly wings. J. Expl Biol. 212 (16), 2705–2719.CrossRefGoogle ScholarPubMed
Maxworthy, T. 1981 The fluid dynamics of insect flight. Annu. Rev. Fluid Mech. 13, 329–350.CrossRefGoogle Scholar
Nakata, T., Liu, H. & Bomphrey, R. J. 2015 A CFD-informed quasi-steady model of flapping-wing aerodynamics. J. Fluid Mech. 783, 323–343.CrossRefGoogle ScholarPubMed
Rayner, J. M. V. 1979 A vortex theory of animal flight. Part 1. The vortex wake of a hovering animal. J. Fluid Mech. 91 (4), 697–730.CrossRefGoogle Scholar
Sane, S. P. 2003 The aerodynamics of insect flight. J. Expl Biol. 206 (23), 4191–4208.CrossRefGoogle ScholarPubMed
Sane, S. P. & Dickinson, M. H. 2001 The control of flight force by a flapping wing: lift and drag production. J. Expl Biol. 204 (15), 2607–2626.Google ScholarPubMed
Sane, S. P. & Dickinson, M. H. 2002 The aerodynamic effects of wing rotation and a revised quasi-steady model of flapping flight. J. Expl Biol. 205, 1087–1096.Google Scholar
Sohn, S.-I. 2018 Inviscid vortex shedding model for the clap and fling motion of insect flights. Phys. Rev. E 98, 033105.Google Scholar
Van Buren, T., Floryan, D., Quinn, D. & Smits, A. J. 2017 Nonsinusoidal gaits for unsteady propulsion. Phys. Rev. Fluids 2, 053101.CrossRefGoogle Scholar
Young, J., Lai, J. C. S. & Germain, C. 2008 Simulation and parameter variation of flapping-wing motion based on dragonfly hovering. AIAA J. 46 (4), 918–924.CrossRefGoogle Scholar
Zheng, L., Hedrick, T. L. & Mittal, R. 2013 A multi-fidelity modelling approach for evaluation and optimization of wing stroke aerodynamics in flapping flight. J. Fluid Mech. 721, 118–154.CrossRefGoogle Scholar

Bhat et al. supplementary movie 1

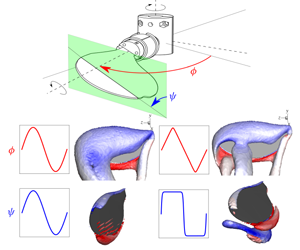
The flow structures over a flapping wing, identified using the iso-Q surfaces and coloured by the normalised spanwise vorticity, are shown for the sweep motion parameters K=0.01 (top) and K=0.99 (bottom). The corresponding variation in the lift coefficient with time is also shown in each case.

Download Bhat et al. supplementary movie 1(Video)
Video 728.7 KB

Bhat et al. supplementary movie 2

The flow structures over a flapping wing, identified using the iso-Q surfaces and coloured by the normalised spanwise vorticity, are shown for the pitch motion parameters C_\psi=0.01 (top) and C_\psi=8 (bottom). The vorticity contours on the spanwise plane at the midspan location are shown in the right column along with the time traces of the lift coefficient.

Download Bhat et al. supplementary movie 2(Video)
Video 1 MB