Hostname: page-component-586b7cd67f-l7hp2 Total loading time: 0 Render date: 2024-11-22T21:26:08.789Z Has data issue: false hasContentIssue false
  • English
  • Français

The effects of Ekman pumping on quasi-geostrophic Rayleigh–Bénard convection

Published online by Cambridge University Press:  16 August 2016

Meredith Plumley ,
Keith Julien ,
Philippe Marti  and
Stephan Stellmach
Meredith Plumley
Affiliation:
Department of Applied Mathematics, University of Colorado, Boulder, CO 80309, USA
Keith Julien*
Affiliation:
Department of Applied Mathematics, University of Colorado, Boulder, CO 80309, USA
Philippe Marti
Affiliation:
Department of Applied Mathematics, University of Colorado, Boulder, CO 80309, USA
Stephan Stellmach
Affiliation:
Institut für Geophysik, Westfälische Wilhelms-Universität Münster, D-48149 Münster, Germany
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Numerical simulations of three-dimensional rapidly rotating Rayleigh–Bénard convection are performed by employing an asymptotic quasi-geostrophic model that incorporates the effects of no-slip boundaries through (i) parametrized Ekman pumping boundary conditions and (ii) a thermal wind boundary layer that regularizes the enhanced thermal fluctuations induced by pumping. The fidelity of the model, obtained by an asymptotic reduction of the Navier–Stokes equations that implicitly enforces a pointwise geostrophic balance, is explored for the first time by comparisons of simulations against the findings of direct numerical simulations (DNS) and laboratory experiments. Results from these methods have established Ekman pumping as the mechanism responsible for significantly enhancing the vertical heat transport. This asymptotic model demonstrates excellent agreement over a range of thermal forcing for Prandtl number 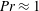$Pr\approx 1$ when compared with results from experiments and DNS at maximal values of their attainable rotation rates, as measured by the Ekman number (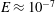$E\approx 10^{-7}$); good qualitative agreement is achieved for 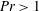$Pr>1$. Similar to studies with stress-free boundaries, four spatially distinct flow morphologies exists. Despite the presence of frictional drag at the upper and/or lower boundaries, a strong non-local inverse cascade of barotropic (i.e. depth-independent) kinetic energy persists in the final regime of geostrophic turbulence and is dominant at large scales. For mixed no-slip/stress-free and no-slip/no-slip boundaries, Ekman friction is found to attenuate the efficiency of the upscale energy transport and, unlike the case of stress-free boundaries, rapidly saturates the barotropic kinetic energy. For no-slip/no-slip boundaries, Ekman friction is strong enough to prevent the development of a coherent dipole vortex condensate. Instead, vortex pairs are found to be intermittent, varying in both time and strength. For all combinations of boundary conditions, a Nastrom–Gage type of spectrum of kinetic energy is found, where the power-law exponent changes from 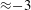${\approx}-3$ to 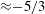${\approx}-5/3$, i.e. from steep to shallow, as the spectral wavenumber increases.

JFM classification

Geophysical and Geological Flows: Geostrophic turbulence Geophysical and Geological Flows: Quasi-geostrophic flows
Type
Papers
Information
Journal of Fluid Mechanics , Volume 803 , 25 September 2016 , pp. 51 - 71
Check for updates
Copyright
© 2016 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Aurnou, J. M., Calkins, M. A., Cheng, J. S., Julien, K., King, E. M., Nieves, D., Soderlund, K. M. & Stellmach, S. 2015 Rotating convective turbulence in Earth and planetary cores. Phys. Earth Planet. Inter. 246, 52–71.CrossRefGoogle Scholar
Busse, F. H. 1970 Thermal instabilities in rapidly rotating systems. J. Fluid Mech. 44, 441–460.Google Scholar
Busse, F. H. 1986 Asymptotic theory of convection in a rotating, cylindrical annulus. J. Fluid Mech. 173, 545–556.CrossRefGoogle Scholar
Calkins, M. A., Julien, K. & Marti, P. 2013 Three-dimensional quasi-geostrophic convection in the rotating cylindrical annulus with steeply sloping endwalls. J. Fluid Mech. 732, 214–244.Google Scholar
Chandrasekhar, S. 1961 Hydrodynamic and Hydromagnetic Stability. Oxford University Press.Google Scholar
Charney, J. 1971 Geostrophic turbulence. J. Atmos. Sci. 28, 1087–1095.2.0.CO;2>CrossRefGoogle Scholar
Charney, J. G. 1948 On the scale of atmospheric motions. Geophys. Publ. 17, 3–17.Google Scholar
Cheng, J. S., Stellmach, S., Ribeiro, A., Grannan, A., King, E. M. & Aurnou, J. M. 2015 Laboratory–numerical models of rapidly rotating convection in planetary cores. Geophys. J. Intl 201, 1–17.CrossRefGoogle Scholar
Ecke, R. E. & Niemela, J. J. 2014 Heat transport in the geostrophic regime of rotating Rayleigh–Bénard convection. Phys. Rev. Lett. 113, 114301.Google Scholar
Favier, B., Silvers, L. J. & Proctor, M. R. E. 2014 Inverse cascade and symmetry breaking in rapidly rotating Boussinesq convection. Phys. Fluids 26, 096605.Google Scholar
Gastine, T., Heimpel, M. & Wicht, J. 2014 Zonal flow scaling in rapidly-rotating compressible convection. Phys. Earth Planet. Inter. 232, 36–50.Google Scholar
Greenspan, H. P. 1968 The Theory of Rotating Fluids. Cambridge University Press.Google Scholar
Guervilly, C., Hughes, D. W. & Jones, C. A. 2014 Large-scale vortices in rapidly rotating Rayleigh–Bénard convection. J. Fluid Mech. 758, 407–435.Google Scholar
Guervilly, C., Hughes, D. W. & Jones, C. A. 2015 Generation of magnetic fields by large-scale vortices in rotating convection. Phys. Rev. E 91 (4), 041001.Google ScholarPubMed
Heimpel, M., Gastine, T. & Wicht, J. 2016 Simulation of deep-seated zonal jets and shallow vortices in gas giant atmospheres. Nat. Geosci. 9 (1), 19–23.Google Scholar
Horn, S. & Shishkina, O. 2015 Toroidal and poloidal energy in rotating Rayleigh–Bénard convection. J. Fluid Mech. 762, 232–255.Google Scholar
Julien, K., Aurnou, J., Calkins, M., Knobloch, E., Marti, P., Stellmach, S. & Vasil, G. 2016 A nonlinear model for rotationally constrained convection with Ekman pumping. J. Fluid Mech. 798, 50–87.CrossRefGoogle Scholar
Julien, K. & Knobloch, E. 2007 Reduced models for fluid flows with strong constraints. J. Math. Phys. 48 (6), 065405.Google Scholar
Julien, K., Knobloch, E., Milliff, R. & Werne, J. 2006 Generalized quasi-geostrophy for spatially anistropic rotationally constrained flows. J. Fluid Mech. 555, 233–274.Google Scholar
Julien, K., Knobloch, E., Rubio, A. M. & Vasil, G. M. 2012a Heat transport in Low-Rossby-number Rayleigh–Bénard convection. Phys. Rev. Lett. 109, 254503.Google Scholar
Julien, K., Knobloch, E. & Werne, J. 1998 A new class of equations for rotationally constrained flows. J. Theor. Comput. Fluid Dyn. 11, 251–261.Google Scholar
Julien, K., Rubio, A. M., Grooms, I. & Knobloch, E. 2012b Statistical and physical balances in low Rossby number Rayleigh–Bénard convection. Geophys. Astrophys. Fluid Dyn. 106 (4–5), 392–428.CrossRefGoogle Scholar
Julien, K. & Watson, M. 2009 Efficient multi-dimensional solution of PDEs using Chebyshev spectral methods. J. Comput. Phys. 228, 1480–1503.CrossRefGoogle Scholar
King, E. M. & Aurnou, J. M. 2013 Turbulent convection in liquid metal with and without rotation. Proc. Natl Acad. Sci. 110 (17), 6688–6693.CrossRefGoogle ScholarPubMed
Kunnen, R. P. J., Ostilla-Mónico, R., van der Poel, E. P., Verzicco, R. & Lohse, D. 2016 Transition to geostrophic convection: the role of the boundary conditions. J. Fluid Mech. 799, 413–432.Google Scholar
Marshall, J. & Schott, F. 1999 Open-ocean convection: observations, theory, and models. Rev. Geophys. 37 (1), 1–64.Google Scholar
Miesch, M. S. 2005 Large-scale dynamics of the convection zone and tachocline. Living Rev. Solar Phys. 2 (1), 2005-1.Google Scholar
Nastrom, G. D. & Gage, K. S. 1985 A climatology of atmospheric wavenumber spectra of wind and temperature observed by commercial aircraft. J. Atmos. Sci. 42 (9), 950–960.Google Scholar
Nieves, D., Rubio, A. M. & Julien, K. 2014 Statistical classification of flow morphology in rapidly rotating Rayleigh–Bénard convection. Phys. Fluids 26 (8), 086602.Google Scholar
Pope, S. B. 2000 Turbulent Flows. Cambridge University Press.Google Scholar
Roberts, P. H. 1968 On the thermal instability of a rotating-fluid sphere containing heat sources. Phil. Trans. R. Soc. Lond. A 263, 93–117.Google Scholar
Rubio, A. M., Julien, K., Knobloch, E. & Weiss, J. B. 2014 Upscale energy transfer in three-dimensional rapidly rotating turbulent convection. Phys. Rev. Lett. 112, 144501.Google Scholar
Schubert, G. & Soderlund, K. M. 2011 Planetary magnetic fields: observations and models. Phys. Earth Planet. Inter. 187 (3), 92–108.Google Scholar
Spalart, P. R., Moser, R. D. & Rogers, M. M. 1991 Spectral methods for the Navier–Stokes equations with one infinite and two periodic directions. J. Comput. Phys. 96, 297–324.CrossRefGoogle Scholar
Sprague, M., Julien, K., Knobloch, E. & Werne, J. 2006 Numerical simulation of an asymptotically reduced system for rotationally constrained convection. J. Fluid Mech. 551, 141–174.CrossRefGoogle Scholar
Stellmach, S. & Hansen, U. 2008 An efficient spectral method for the simulation of dynamos in Cartesian geometry and its implementation on massively parallel computers. Geochem. Geophys. Geosyst. 9 (5), Q05003.Google Scholar
Stellmach, S., Lischper, M., Julien, K., Vasil, G., Cheng, J. S., Ribeiro, A., King, E. M. & Aurnou, J. M. 2014 Approaching the asymptotic regime of rapidly rotating convection: boundary layers versus interior dynamics. Phys. Rev. Lett. 113, 254501.Google Scholar
Yadav, R. K., Gastine, T., Christensen, U. R. & Reiners, A. 2015 Formation of starspots in self-consistent global dynamo models: polar spots on cool stars. Astron. Astrophys. 573, A68.Google Scholar