Published online by Cambridge University Press: 30 March 2012
Previous experimental studies have shown that the steady recirculation bubble that forms as the flow separates at the leading-edge corner of a long plate, becomes unsteady at relatively low Reynolds numbers of only a few hundreds. The reattaching shear layer irregularly releases two-dimensional vortices, which quickly undergo three-dimensional transition. Similar to the flow over a backward-facing step, this flow is globally stable at such Reynolds numbers, with transition to a steady three-dimensional flow as the first global instability to occur as the Reynolds number is increased to 393. Hence, it appears that the observed flow behaviour is governed by transient growth of optimal two-dimensional transiently growing perturbations (constructed from damped global modes) rather than a single three-dimensional unstable global mode. This paper quantifies the details of the transient growth of two- and three-dimensional optimal perturbations, and compares the predictions to other related cases examined recently. The optimal perturbation modes are shown to be highly concentrated in amplitude in the vicinity of the leading-edge corners and evolve to take the local shape of a Kelvin–Helmholtz shear-layer instability further downstream. However, the dominant mode reaches a maximum amplitude downstream of the position of the reattachment point of the shear layer. The maximum energy growth increases at 2.5 decades for each increment in Reynolds number of 100. Maximum energy growth of the optimal perturbation mode at a Reynolds number of 350 is greater than 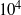 , which is typically an upper limit of the Reynolds number range over which it is possible to observe steady flow experimentally. While transient growth analysis concentrates on the evolution of wavepackets rather than continuous forcing, this appears consistent with longitudinal turbulence levels of up to 1 % for some water tunnels, and the fact that the optimal mode is highly concentrated close to the leading-edge corner so that an instantaneous projection of a perturbation field from a noisy inflow onto the optimal mode can be significant. Indeed, direct simulations with inflow noise reveal that a root-mean-square noise level of just 0.1 % is sufficient to trigger some unsteadiness at
, which is typically an upper limit of the Reynolds number range over which it is possible to observe steady flow experimentally. While transient growth analysis concentrates on the evolution of wavepackets rather than continuous forcing, this appears consistent with longitudinal turbulence levels of up to 1 % for some water tunnels, and the fact that the optimal mode is highly concentrated close to the leading-edge corner so that an instantaneous projection of a perturbation field from a noisy inflow onto the optimal mode can be significant. Indeed, direct simulations with inflow noise reveal that a root-mean-square noise level of just 0.1 % is sufficient to trigger some unsteadiness at 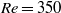 , while a 0.5 % level results in sustained shedding. Three-dimensional optimal perturbation mode analysis was also performed showing that at
, while a 0.5 % level results in sustained shedding. Three-dimensional optimal perturbation mode analysis was also performed showing that at 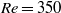 , the optimal mode has a spanwise wavelength of 11.7 plate thicknesses and is amplified 20 % more than the two-dimensional optimal disturbance. The evolved three-dimensional mode shows strong streamwise vortical structures aligned at a shallow angle to the plate top surface.
, the optimal mode has a spanwise wavelength of 11.7 plate thicknesses and is amplified 20 % more than the two-dimensional optimal disturbance. The evolved three-dimensional mode shows strong streamwise vortical structures aligned at a shallow angle to the plate top surface.