Article contents
Effect of turbulent fluctuations on the drag and lift forces on a towed sphere and its boundary layer
Published online by Cambridge University Press: 13 March 2013
Abstract
The impact of turbulent fluctuations on the forces exerted by a fluid on a towed spherical particle is investigated by means of high-resolution direct numerical simulations. The measurements are carried out using a novel scheme to integrate the two-way coupling between the particle and the incompressible surrounding fluid flow maintained in a high-Reynolds-number turbulent regime. The main idea consists of combining a Fourier pseudo-spectral method for the fluid with an immersed-boundary technique to impose the no-slip boundary condition on the surface of the particle. This scheme is shown to converge as the power 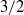 $3/ 2$ of the spatial resolution. This behaviour is explained by the
$3/ 2$ of the spatial resolution. This behaviour is explained by the 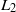 ${L}_{2} $ convergence of the Fourier representation of a velocity field displaying discontinuities of its derivative. Benchmarking of the code is performed by measuring the drag and lift coefficients and the torque-free rotation rate of a spherical particle in various configurations of an upstream-laminar carrier flow. Such studies show a good agreement with experimental and numerical measurements from other groups. A study of the turbulent wake downstream of the sphere is also reported. The mean velocity deficit is shown to behave as the inverse of the distance from the particle, as predicted from classical similarity analysis. This law is reinterpreted in terms of the principle of ‘permanence of large eddies’ that relates infrared asymptotic self-similarity to the law of decay of energy in homogeneous turbulence. The developed method is then used to attack the problem of an upstream flow that is in a developed turbulent regime. It is shown that the average drag force increases as a function of the turbulent intensity and the particle Reynolds number. This increase is significantly larger than predicted by standard drag correlations based on laminar upstream flows. It is found that the relevant parameter is the ratio of the viscous boundary layer thickness to the dissipation scale of the ambient turbulent flow. The drag enhancement can be motivated by the modification of the mean velocity and pressure profile around the sphere by small-scale turbulent fluctuations. It is demonstrated that the variance of the drag force fluctuations can be modelled by means of standard drag correlations. Temporal correlations of the drag and lift forces are also presented.
${L}_{2} $ convergence of the Fourier representation of a velocity field displaying discontinuities of its derivative. Benchmarking of the code is performed by measuring the drag and lift coefficients and the torque-free rotation rate of a spherical particle in various configurations of an upstream-laminar carrier flow. Such studies show a good agreement with experimental and numerical measurements from other groups. A study of the turbulent wake downstream of the sphere is also reported. The mean velocity deficit is shown to behave as the inverse of the distance from the particle, as predicted from classical similarity analysis. This law is reinterpreted in terms of the principle of ‘permanence of large eddies’ that relates infrared asymptotic self-similarity to the law of decay of energy in homogeneous turbulence. The developed method is then used to attack the problem of an upstream flow that is in a developed turbulent regime. It is shown that the average drag force increases as a function of the turbulent intensity and the particle Reynolds number. This increase is significantly larger than predicted by standard drag correlations based on laminar upstream flows. It is found that the relevant parameter is the ratio of the viscous boundary layer thickness to the dissipation scale of the ambient turbulent flow. The drag enhancement can be motivated by the modification of the mean velocity and pressure profile around the sphere by small-scale turbulent fluctuations. It is demonstrated that the variance of the drag force fluctuations can be modelled by means of standard drag correlations. Temporal correlations of the drag and lift forces are also presented.
- Type
- Papers
- Information
- Copyright
- ©2013 Cambridge University Press
References
- 58
- Cited by


