Published online by Cambridge University Press: 24 May 2016
The mechanism of surface-charge convection, quantified by the electric Reynolds number 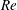 $Re$, renders the Melcher–Taylor electrohydrodynamic model inherently nonlinear, with the electrostatic problem coupled to the flow. Because of this nonlinear coupling, the settling speed of a drop under a uniform electric field differs from that in its absence. This difference was calculated by Xu & Homsy (J. Fluid Mech., vol. 564, 2006, pp. 395–414) assuming small
$Re$, renders the Melcher–Taylor electrohydrodynamic model inherently nonlinear, with the electrostatic problem coupled to the flow. Because of this nonlinear coupling, the settling speed of a drop under a uniform electric field differs from that in its absence. This difference was calculated by Xu & Homsy (J. Fluid Mech., vol. 564, 2006, pp. 395–414) assuming small 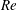 $Re$. We here address the same problem using a different route, considering the case where the applied electric field is weak in the sense that the magnitude of the associated electrohydrodynamic velocity is small compared with the settling velocity. As convection is determined at leading order by the well-known flow associated with pure settling, the electrostatic problem becomes linear for arbitrary value of
$Re$. We here address the same problem using a different route, considering the case where the applied electric field is weak in the sense that the magnitude of the associated electrohydrodynamic velocity is small compared with the settling velocity. As convection is determined at leading order by the well-known flow associated with pure settling, the electrostatic problem becomes linear for arbitrary value of 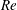 $Re$. The electrohydrodynamic correction to the settling speed is then provided as a linear functional of the electric-stress distribution associated with that problem. Calculation of the settling speed eventually amounts to the solution of a difference equation governing the respective coefficients in a spherical harmonics expansion of the electric potential. It is shown that, despite the present weak-field assumption, our model reproduces the small-
$Re$. The electrohydrodynamic correction to the settling speed is then provided as a linear functional of the electric-stress distribution associated with that problem. Calculation of the settling speed eventually amounts to the solution of a difference equation governing the respective coefficients in a spherical harmonics expansion of the electric potential. It is shown that, despite the present weak-field assumption, our model reproduces the small-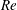 $Re$ approximation of Xu and Homsy as a particular case. For finite
$Re$ approximation of Xu and Homsy as a particular case. For finite 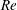 $Re$, inspection of the difference equation reveals a singularity at the critical
$Re$, inspection of the difference equation reveals a singularity at the critical 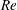 $Re$-value
$Re$-value 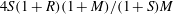 $4S(1+R)(1+M)/(1+S)M$, wherein
$4S(1+R)(1+M)/(1+S)M$, wherein 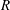 $R$,
$R$, 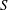 $S$ and
$S$ and 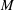 $M$ respectively denote the ratios of resistivity, permittivity and viscosity values in the suspending and drop phases, as defined by Melcher & Taylor (Annu. Rev. Fluid Mech., vol. 1, 1969, pp. 111–146). Straightforward numerical solutions of this equation for electric Reynolds numbers smaller than the critical value reveal a non-monotonic dependence of the settling speed upon the electric field magnitude, including a transition from velocity enhancement to velocity decrement.
$M$ respectively denote the ratios of resistivity, permittivity and viscosity values in the suspending and drop phases, as defined by Melcher & Taylor (Annu. Rev. Fluid Mech., vol. 1, 1969, pp. 111–146). Straightforward numerical solutions of this equation for electric Reynolds numbers smaller than the critical value reveal a non-monotonic dependence of the settling speed upon the electric field magnitude, including a transition from velocity enhancement to velocity decrement.