Hostname: page-component-cd9895bd7-mkpzs Total loading time: 0 Render date: 2024-12-27T10:57:25.696Z Has data issue: false hasContentIssue false
  • English
  • Français

The effect of streaks on the instability of jets

Published online by Cambridge University Press:  08 January 2021

Chuhan Wang Open the ORCID record for Chuhan Wang [Opens in a new window] ,
Lutz Lesshafft Open the ORCID record for Lutz Lesshafft [Opens in a new window] ,
André V. G. Cavalieri Open the ORCID record for André V. G. Cavalieri [Opens in a new window]  and
Peter Jordan Open the ORCID record for Peter Jordan [Opens in a new window]
Chuhan Wang*
Affiliation:
Laboratoire d'Hydrodynamique, CNRS/Ecole Polytechnique/Institut Polytechnique de Paris, 91120Palaiseau, France
Lutz Lesshafft
Affiliation:
Laboratoire d'Hydrodynamique, CNRS/Ecole Polytechnique/Institut Polytechnique de Paris, 91120Palaiseau, France
André V. G. Cavalieri
Affiliation:
Instituto Tecnológico de Aeronáutica, São José dos Campos, SP12228-900, Brazil
Peter Jordan
Affiliation:
Institut Pprime, CNRS/Université de Poitiers/ENSMA, 86000Poitiers, France
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

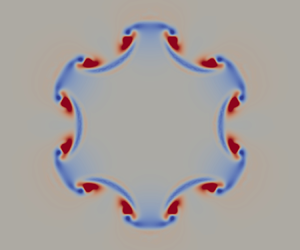
The presence of elongated streaks of high and low streamwise velocity in the shear layer of circular jets breaks the axisymmetry of their steady-state solution. If the streaks are considered to be part of the base flow, for the purpose of linear instability analysis, the instability eigenmodes are thus affected by their presence. The resulting changes of growth rate and spatial shapes of eigenmodes, related to the shear instability in jets, are investigated here for parallel base flows. Optimal streamwise vortices (‘rolls’) with prescribed azimuthal periodicity are computed, such that the transient temporal growth of the streaks that they produce is maximal. The presence of finite-amplitude streaks requires the formulation of eigenvalue problems in a two-dimensional cross-plane. Sinuous rolls and streaks are found to have a stabilising effect on the Kelvin–Helmholtz instability, whereas the varicose rolls and streaks have a destabilising effect. Absolute instability is not found to occur. This work shows that the effects of rolls and streaks need to be taken into account for more precise modelling of jet instability.

JFM classification

Wakes/Jets: Jets Instability: Absolute/convective instability
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 910 , 10 March 2021 , A14
Check for updates
Copyright
© The Author(s), 2021. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

Boujo, E., Fani, A. & Gallaire, F. 2015 Second-order sensitivity of parallel shear flows and optimal spanwise-periodic flow modifications. J. Fluid Mech. 782, 491–514.CrossRefGoogle Scholar
Boujo, E., Fani, A. & Gallaire, F. 2019 Second-order sensitivity in the cylinder wake: optimal spanwise-periodic wall actuation and wall deformation. Phys. Rev. Fluids 4, 053901.CrossRefGoogle Scholar
Brandt, L., Cossu, C., Chomaz, J.-M., Huerre, P. & Henningson, D. S. 2003 On the convectively unstable nature of optimal streaks in boundary layers. J. Fluid Mech. 485, 221–242.CrossRefGoogle Scholar
Butler, K. M. & Farrell, B. F. 1992 Three-dimensional optimal perturbations in viscous shear flow. Phys. Fluids A 4 (8), 1637–1650.CrossRefGoogle Scholar
Cavalieri, A. V. G., Jordan, P. & Lesshafft, L. 2019 Wave-packet models for jet dynamics and sound radiation. Appl. Mech. Rev. 71 (2), 020802.CrossRefGoogle Scholar
Chomaz, J.-M. 2005 Global instabilities in spatially developing flows: non-normality and nonlinearity. Annu. Rev. Fluid Mech. 37, 357–392.CrossRefGoogle Scholar
Del Guercio, G., Cossu, C. & Pujals, G. 2014 Stabilizing effect of optimally amplified streaks in parallel wakes. J. Fluid Mech. 739, 37–56.CrossRefGoogle Scholar
Hill, D. 1992 A theoretical approach for analyzing the restabilization of wakes. In 30th Aerospace Sciences Meeting and Exhibit, p. 67.Google Scholar
Huerre, P. & Monkewitz, P. A. 1990 Local and global instabilities in spatially developing flows. Annu. Rev. Fluid Mech. 22 (1), 473–537.CrossRefGoogle Scholar
Hwang, Y. & Choi, H. 2006 Control of absolute instability by basic-flow modification in a parallel wake at low Reynolds number. J. Fluid Mech. 560, 465–475.CrossRefGoogle Scholar
Hwang, Y. & Cossu, C. 2010 Self-sustained process at large scales in turbulent channel flow. Phys. Rev. Lett. 105 (4), 044505.CrossRefGoogle ScholarPubMed
Jiménez, J. 2013 How linear is wall-bounded turbulence? Phys. Fluids 25 (11), 110814.CrossRefGoogle Scholar
Jiménez-González, J. I. & Brancher, P. 2017 Transient energy growth of optimal streaks in parallel round jets. Phys. Fluids 29 (11), 114101.CrossRefGoogle Scholar
Jordan, P. & Colonius, T. 2013 Wave packets and turbulent jet noise. Annu. Rev. Fluid Mech. 45, 173–195.CrossRefGoogle Scholar
Kantharaju, J., Courtier, R., Leclaire, B. & Jacquin, L. 2020 Interactions of large-scale structures in the near field of round jets at high Reynolds numbers. J. Fluid Mech. 888, A8.CrossRefGoogle Scholar
Lajús, F. C., Sinha, A., Cavalieri, A. V. G., Deschamps, C. J. & Colonius, T. 2019 Spatial stability analysis of subsonic corrugated jets. J. Fluid Mech. 876, 766–791.CrossRefGoogle Scholar
Landahl, M. T. 1975 Wave breakdown and turbulence. SIAM J. Appl. Maths 28 (4), 735–756.CrossRefGoogle Scholar
Lesshafft, L. & Huerre, P. 2007 Linear impulse response in hot round jets. Phys. Fluids 19 (2), 024102.CrossRefGoogle Scholar
Lesshafft, L. & Marquet, O. 2010 Optimal velocity and density profiles for the onset of absolute instability in jets. J. Fluid Mech. 662, 398–408.CrossRefGoogle Scholar
Logg, A. & Wells, G. 2010 Dolfin: automated finite element computing. ACM Trans. Math. Softw. 37 (2), 20.CrossRefGoogle Scholar
Marant, M. & Cossu, C. 2018 Influence of optimally amplified streamwise streaks on the Kelvin–Helmholtz instability. J. Fluid Mech. 838, 478–500.CrossRefGoogle Scholar
Marquet, O., Sipp, D. & Jacquin, L. 2008 Sensitivity analysis and passive control of cylinder flow. J. Fluid Mech. 615, 221.CrossRefGoogle Scholar
Michalke, A. 1971 Instabilität eines kompressiblen runden Freistrahls unter Berücksichtigung des Einflusses der Strahlgrenzschichtdicke. Z. Flugwiss. 19, 319.Google Scholar
Nastro, G., Fontane, J. & Joly, L. 2020 Optimal perturbations in viscous round jets subject to Kelvin–Helmholtz instability. J. Fluid Mech. 900, 1–25.CrossRefGoogle Scholar
Nogueira, P. A. S., Cavalieri, A. V. G., Jordan, P. & Jaunet, V. 2019 Large-scale streaky structures in turbulent jets. J. Fluid Mech. 873, 211–237.CrossRefGoogle Scholar
Park, J., Hwang, Y. & Cossu, C. 2011 On the stability of large-scale streaks in turbulent Couette and Poiseuille flows. C. R. Méc. 339 (1), 1–5.CrossRefGoogle Scholar
Pickering, E., Rigas, G., Nogueira, P. A. S., Cavalieri, A. V. G., Schmidt, O. T. & Colonius, T. 2020 Lift-up, Kelvin–Helmholtz and Orr mechanisms in turbulent jets. J. Fluid Mech. 896, A2.CrossRefGoogle Scholar
Schmid, P. J. & Henningson, D. S. 2001 Stability and Transition in Shear Flows. Springer.CrossRefGoogle Scholar
Tammisola, O., Giannetti, F., Citro, V. & Juniper, M. P. 2014 Second-order perturbation of global modes and implications for spanwise wavy actuation. J. Fluid Mech. 755, 314–335.CrossRefGoogle Scholar
Waleffe, F. 1997 On a self-sustaining process in shear flows. Phys. Fluids 9 (4), 883–900.CrossRefGoogle Scholar