Hostname: page-component-78c5997874-lj6df Total loading time: 0 Render date: 2024-11-19T04:03:33.581Z Has data issue: false hasContentIssue false
  • English
  • Français

The effect of small viscosity and diffusivity on the marginal stability of stably stratified shear flows

Published online by Cambridge University Press:  15 August 2013

S. A. Thorpe ,
W. D. Smyth  and
Lin Li
S. A. Thorpe*
Affiliation:
School of Ocean Sciences, Bangor University, Menai Bridge, Anglesey LL59 5AB, UK
W. D. Smyth
Affiliation:
College of Oceanic and Atmospheric Sciences, Oregon State University, Corvallis, OR 97331-5503, USA
Lin Li
Affiliation:
College of Oceanic and Atmospheric Sciences, Oregon State University, Corvallis, OR 97331-5503, USA
*
†Addresses for correspondence: ‘Bodfryn’, Glanrafon, Llangoed, Anglesey LL58 8PH, UK. Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

The effect of non-zero, but small, viscosity and diffusivity on the marginal stability of a stably stratified shear flow is examined by making perturbations around the neutral solution for an inviscid and non-diffusive flow. The results apply to turbulent flows in which horizontal and vertical turbulent transports of momentum and buoyancy are represented by eddy coefficients of viscosity and diffusivity that vary in the vertical ($z$) direction. General expressions are derived for the modified phase speed and the growth rate of small disturbances as a function of wavenumber. To first order in their coefficients, the effect on the phase speed of adding viscosity and diffusivity is zero. Growth rates are found for two mean flows when the horizontal or vertical coefficients of viscosity and diffusivity vary in $z$ in such a way that the rates can be found analytically. The first flow, denoted as a ‘Holmboe flow’, has a velocity and density interface: the mean horizontal velocity and the density are both proportional to 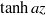$\tanh az$, where $a$ is proportional to the inverse of the interface thickness. The second, ‘Drazin flow’, has a similar velocity variation in $z$ but uniform density gradient. The analytical results compare favourably with numerical calculations. Small horizontal coefficients of viscosity and diffusivity may affect disturbances to the flow in opposite ways. Although the effect of uniform vertical coefficients of viscosity is to decrease the growth rates, and uniform vertical coefficients of diffusivity increase them, cases are found in which, with suitably chosen $z$ dependence, vertical coefficients of viscosity (or diffusivity) may cause a previously neutral disturbance to grow (or to diminish); viscosity may destabilize a stably stratified shear flow. The introduction of viscosity and diffusivity may consequently increase the critical Richardson number to a value exceeding 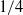$1/ 4$. While some patterns of behaviour are apparent, no simple rule appears to hold about whether flows that are neutral in the absence of these effects (viscosity or diffusivity) will be stabilized or destabilized when they are added. One such rule, namely our conjecture that viscosity is always stabilizing and that diffusivity is destabilizing, is explicitly refuted.

JFM classification

Geophysical and Geological Flows: Geophysical and Geological Flows Instability: Instability Turbulent Flows: Stratified turbulence
Type
Papers
Information
Journal of Fluid Mechanics , Volume 731 , 25 September 2013 , pp. 461 - 476
Copyright
©2013 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Abramowitz, M. & Stegun, I. A. 1965 Handbook of Mathematical Functions. Dover, 1046 pp.Google Scholar
Banks, W. H. H., Drazin, P. G. & Zaturska, M. B. 1976 On the normal modes of parallel flow of inviscid stratified fluid. J. Fluid Mech. 75, 149–171.CrossRefGoogle Scholar
Drazin, P. G. 1958 The stability of a shear layer in an unbounded heterogeneous inviscid fluid. J. Fluid Mech. 4, 214–224.CrossRefGoogle Scholar
Drazin, P. G. & Howard, L. N. 1966 Hydrodynamic stability of parallel flow of inviscid fluid. In Advances in Applied Mechanics (ed. Kuerti, G.), vol. 7, pp. 1–89. Academic.Google Scholar
Drazin, P. G. & Reid, W. H. 1981 Hydrodynamic Stability. Cambridge University Press, 525 pp.Google Scholar
Hazel, P. 1972 Numerical studies of the stability of inviscid stratified shear flows. J. Fluid Mech. 51, 39–61.CrossRefGoogle Scholar
Howard, L. N. 1961 Note on a paper by John W. Miles. J. Fluid Mech. 10, 509–512.CrossRefGoogle Scholar
Howard, L. N. 1963 Neutral curves and stability boundaries in stratified flow. J. Fluid Mech. 16, 333–342.CrossRefGoogle Scholar
Huppert, H. E. 1973 On Howard’s technique for perturbing neutral solutions of the Taylor–Goldstein equation. J. Fluid Mech. 57, 361–368.CrossRefGoogle Scholar
Kantha, L. H. & Clayson, C. 2000 Small Scale Processes in Geophysical Flows. Academic, 889pp.Google Scholar
Liu, Z., Thorpe, S. A. & Smyth, W. D. 2012 Instability and hydraulics of turbulent stratified shear flows. J. Fluid Mech. 695, 235–256.CrossRefGoogle Scholar
Maslowe, S. & Thompson, J. 1971 Stability of a stratified free shear layer. Phys. Fluids 14, 453–458.CrossRefGoogle Scholar
Matthews, P. C. 1988 A model for the onset of penetrative convection. J. Fluid Mech. 188, 571–583.CrossRefGoogle Scholar
Miles, J. W. 1961 On the stability of heterogeneous shear flows. J. Fluid Mech. 10, 496–508.CrossRefGoogle Scholar
Osborn, T. R. 1980 Estimates of the local rate of vertical diffusion from dissipation measurements. J. Phys. Oceanogr. 10, 83–89.2.0.CO;2>CrossRefGoogle Scholar
Smyth, W. D. & Moum, J. N. 2000 Length scales of turbulence in stably stratified mixing layers. Phys. Fluids 12, 1327–1342.CrossRefGoogle Scholar
Smyth, W. D., Moum, J. N., Li, L. & Thorpe, S. A. 2014 The diurnal cycle of shear instability in the upper Equatorial Pacific. J. Phys. Oceanogr. (submitted).Google Scholar
Smyth, W. D., Moum, J. N. & Nash, J. D. 2011 Narrowband, high-frequency oscillations at the equator. Part II. Properties of shear instabilities. J. Phys. Oceanogr. 41, 412–428.CrossRefGoogle Scholar
Thorpe, S. A. 1969 Neutral eigensolutions of the stability equation for stratified shear flow. J. Fluid Mech. 36, 673–683.CrossRefGoogle Scholar
Thorpe, S. A. 1973 Experiments on instability and turbulence in a stratified shear flow. J. Fluid Mech. 61, 731–751.CrossRefGoogle Scholar
Woods, J. D. 1968 Wave-induced shear instability in the summer thermocline. J. Fluid Mech. 32, 791–800.CrossRefGoogle Scholar