Published online by Cambridge University Press: 31 October 2014
This paper exploits the turbulent flow control method using streamwise travelling waves (Quadrio et al. J. Fluid Mech., vol. 627, 2009, pp. 161–178) to study the effect of Reynolds number on turbulent skin-friction drag reduction. Direct numerical simulations (DNS) of a turbulent channel flow subjected to the streamwise travelling waves of spanwise wall velocity have been performed at Reynolds numbers ranging from 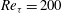 $\mathit{Re}_{{\it\tau}}=200$ to 1600. To the best of the authors’ knowledge, this is the highest Reynolds number attempted with DNS for this type of flow control. The present DNS results confirm that the effectiveness of drag reduction deteriorates, and the maximum drag reduction achieved by travelling waves decreases significantly as the Reynolds number increases. The intensity of both the drag reduction and drag increase is reduced with the Reynolds number. Another important finding is that the value of the optimal control parameters changes, even in wall units, when the Reynolds number is increased. This trend is observed for the wall oscillation, stationary wave, and streamwise travelling wave cases. This implies that, when the control parameters used are close to optimal values found at a lower Reynolds number, the drag reduction deteriorates rapidly with increased Reynolds number. In this study, the effect of Reynolds number for the travelling wave is quantified using a scaling in the form
$\mathit{Re}_{{\it\tau}}=200$ to 1600. To the best of the authors’ knowledge, this is the highest Reynolds number attempted with DNS for this type of flow control. The present DNS results confirm that the effectiveness of drag reduction deteriorates, and the maximum drag reduction achieved by travelling waves decreases significantly as the Reynolds number increases. The intensity of both the drag reduction and drag increase is reduced with the Reynolds number. Another important finding is that the value of the optimal control parameters changes, even in wall units, when the Reynolds number is increased. This trend is observed for the wall oscillation, stationary wave, and streamwise travelling wave cases. This implies that, when the control parameters used are close to optimal values found at a lower Reynolds number, the drag reduction deteriorates rapidly with increased Reynolds number. In this study, the effect of Reynolds number for the travelling wave is quantified using a scaling in the form 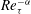 $\mathit{Re}_{{\it\tau}}^{-{\it\alpha}}$. No universal constant is found for the scaling parameter
$\mathit{Re}_{{\it\tau}}^{-{\it\alpha}}$. No universal constant is found for the scaling parameter  ${\it\alpha}$. Instead, the scaling parameter
${\it\alpha}$. Instead, the scaling parameter  ${\it\alpha}$ has a wide range of values depending on the flow control conditions. Further Reynolds number scaling issues are discussed. Turbulent statistics are analysed to explain a weaker drag reduction observed at high Reynolds numbers. The changes in the Stokes layer and also the mean and root-mean-squared (r.m.s.) velocity with the Reynolds number are also reported. The Reynolds shear stress analysis suggests an interesting possibility of a finite drag reduction at very high Reynolds numbers.
${\it\alpha}$ has a wide range of values depending on the flow control conditions. Further Reynolds number scaling issues are discussed. Turbulent statistics are analysed to explain a weaker drag reduction observed at high Reynolds numbers. The changes in the Stokes layer and also the mean and root-mean-squared (r.m.s.) velocity with the Reynolds number are also reported. The Reynolds shear stress analysis suggests an interesting possibility of a finite drag reduction at very high Reynolds numbers.