Article contents
Effect of non-parallel mean flow on the Green’s function for predicting the low-frequency sound from turbulent air jets
Published online by Cambridge University Press: 13 February 2012
Abstract
It is now well-known that there is an exact formula relating the far-field jet noise spectrum to the convolution product of a propagator (that accounts for the mean flow interactions) and a generalized Reynolds stress autocovariance tensor (that accounts for the turbulence fluctuations). The propagator depends only on the mean flow and an adjoint vector Green’s function for a particular form of the linearized Euler equations. Recent numerical calculations of Karabasov, Bogey & Hynes (AIAA Paper 2011-2929) for a Mach 0.9 jet show use of the true non-parallel flow Green’s function rather than the more conventional locally parallel flow result leads to a significant increase in the predicted low-frequency sound radiation at observation angles close to the downstream jet axis. But the non-parallel flow appears to have little effect on the sound radiated at 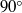 to the downstream axis. The present paper is concerned with the effects of non-parallel mean flows on the adjoint vector Green’s function. We obtain a low-frequency asymptotic solution for that function by solving a very simple second-order hyperbolic equation for a composite dependent variable (which is directly proportional to a pressure-like component of this Green’s function and roughly corresponds to the strength of a monopole source within the jet). Our numerical calculations show that this quantity remains fairly close to the corresponding parallel flow result at low Mach numbers and that, as expected, it converges to that result when an appropriately scaled frequency parameter is increased. But the convergence occurs at progressively higher frequencies as the Mach number increases and the supersonic solution never actually converges to the parallel flow result in the vicinity of a critical- layer singularity that occurs in that solution. The dominant contribution to the propagator comes from the radial derivative of a certain component of the adjoint vector Green’s function. The non-parallel flow has a large effect on this quantity, causing it (and, therefore, the radiated sound) to increase at subsonic speeds and decrease at supersonic speeds. The effects of acoustic source location can be visualized by plotting the magnitude of this quantity, as function of position. These ‘altitude plots’ (which represent the intensity of the radiated sound as a function of source location) show that while the parallel flow solutions exhibit a single peak at subsonic speeds (when the source point is centred on the initial shear layer), the non-parallel solutions exhibit a double peak structure, with the second peak occurring about two potential core lengths downstream of the nozzle. These results are qualitatively consistent with the numerical calculations reported in Karabasov et al. (2011).
to the downstream axis. The present paper is concerned with the effects of non-parallel mean flows on the adjoint vector Green’s function. We obtain a low-frequency asymptotic solution for that function by solving a very simple second-order hyperbolic equation for a composite dependent variable (which is directly proportional to a pressure-like component of this Green’s function and roughly corresponds to the strength of a monopole source within the jet). Our numerical calculations show that this quantity remains fairly close to the corresponding parallel flow result at low Mach numbers and that, as expected, it converges to that result when an appropriately scaled frequency parameter is increased. But the convergence occurs at progressively higher frequencies as the Mach number increases and the supersonic solution never actually converges to the parallel flow result in the vicinity of a critical- layer singularity that occurs in that solution. The dominant contribution to the propagator comes from the radial derivative of a certain component of the adjoint vector Green’s function. The non-parallel flow has a large effect on this quantity, causing it (and, therefore, the radiated sound) to increase at subsonic speeds and decrease at supersonic speeds. The effects of acoustic source location can be visualized by plotting the magnitude of this quantity, as function of position. These ‘altitude plots’ (which represent the intensity of the radiated sound as a function of source location) show that while the parallel flow solutions exhibit a single peak at subsonic speeds (when the source point is centred on the initial shear layer), the non-parallel solutions exhibit a double peak structure, with the second peak occurring about two potential core lengths downstream of the nozzle. These results are qualitatively consistent with the numerical calculations reported in Karabasov et al. (2011).
JFM classification
- Type
- Papers
- Information
- Copyright
- Copyright © Cambridge University Press 2012
Footnotes
Present address: Johns Hopkins University, Department of Mechanical Engineering, Baltimore, MD 21218, USA
References
- 25
- Cited by


