Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Thøgersen, Kjetil
and
Dabrowski, Marcin
2017.
Mixing of the fluid phase in slowly sheared particle suspensions of cylinders.
Journal of Fluid Mechanics,
Vol. 818,
Issue. ,
p.
807.
Rallabandi, Bhargav
Hilgenfeldt, Sascha
and
Stone, Howard A.
2017.
Hydrodynamic force on a sphere normal to an obstacle due to a non-uniform flow.
Journal of Fluid Mechanics,
Vol. 818,
Issue. ,
p.
407.
Ramaswamy, Meera
Lin, Neil Y. C.
Leahy, Brian D.
Ness, Christopher
Fiore, Andrew M.
Swan, James W.
and
Cohen, Itai
2017.
How Confinement-Induced Structures Alter the Contribution of Hydrodynamic and Short-Ranged Repulsion Forces to the Viscosity of Colloidal Suspensions.
Physical Review X,
Vol. 7,
Issue. 4,
Guazzelli, Élisabeth
Radjai, F.
Nezamabadi, S.
Luding, S.
and
Delenne, J.Y.
2017.
Rheology of dense suspensions of non colloidal particles.
EPJ Web of Conferences,
Vol. 140,
Issue. ,
p.
01001.
Dbouk, T.
2018.
Heat transfer and shear-induced migration in dense non-Brownian suspension flows: modelling and simulation.
Journal of Fluid Mechanics,
Vol. 840,
Issue. ,
p.
432.
Arietaleaniz, S.
Malgaretti, P.
Pagonabarraga, I.
and
Hidalgo, R. C.
2018.
Rheological behavior of colloidal suspension with long-range interactions.
Physical Review E,
Vol. 98,
Issue. 4,
Seto, Ryohei
and
Giusteri, Giulio G.
2018.
Normal stress differences in dense suspensions.
Journal of Fluid Mechanics,
Vol. 857,
Issue. ,
p.
200.
Guazzelli, Élisabeth
and
Pouliquen, Olivier
2018.
Rheology of dense granular suspensions.
Journal of Fluid Mechanics,
Vol. 852,
Issue. ,
Roht, Y. L.
Ippolito, I.
Hulin, J. P.
Salin, D.
and
Gauthier, G.
2018.
Stripes instability of an oscillating non-Brownian iso-dense suspension of spheres.
EPL (Europhysics Letters),
Vol. 121,
Issue. 5,
p.
54002.
Dbouk, T.
and
Habchi, C.
2019.
On the mixing enhancement in concentrated non-colloidal neutrally buoyant suspensions of rigid particles using helical coiled and chaotic twisted pipes: A numerical investigation.
Chemical Engineering and Processing - Process Intensification,
Vol. 141,
Issue. ,
p.
107540.
Sivadasan, Vishnu
Lorenz, Eric
Hoekstra, Alfons G.
and
Bonn, Daniel
2019.
Shear thickening of dense suspensions: The role of friction.
Physics of Fluids,
Vol. 31,
Issue. 10,
Chèvremont, William
Chareyre, Bruno
and
Bodiguel, Hugues
2019.
Quantitative study of the rheology of frictional suspensions: Influence of friction coefficient in a large range of viscous numbers.
Physical Review Fluids,
Vol. 4,
Issue. 6,
Singha, Sagnik
Malipeddi, Abhilash Reddy
Zurita-Gotor, Mauricio
Sarkar, Kausik
Shen, Kevin
Loewenberg, Michael
Migler, Kalman B.
and
Blawzdziewicz, Jerzy
2019.
Mechanisms of spontaneous chain formation and subsequent microstructural evolution in shear-driven strongly confined drop monolayers.
Soft Matter,
Vol. 15,
Issue. 24,
p.
4873.
Sarabian, Mohammad
Firouznia, Mohammadhossein
Metzger, Bloen
and
Hormozi, Sarah
2019.
Fully developed and transient concentration profiles of particulate suspensions sheared in a cylindrical Couette cell.
Journal of Fluid Mechanics,
Vol. 862,
Issue. ,
p.
659.
Bertocchi, Michael J.
Vang, Pearl
Balow, Robert B.
Wynne, James H.
and
Lundin, Jeffrey G.
2019.
Enhanced Mechanical Damping in Electrospun Polymer Fibers with Liquid Cores: Applications to Sound Damping.
ACS Applied Polymer Materials,
Vol. 1,
Issue. 8,
p.
2068.
Zhou, Gedi
and
Prosperetti, Andrea
2020.
Inertial effects in shear flow of a fluid-particle mixture: Resolved simulations.
Physical Review Fluids,
Vol. 5,
Issue. 8,
More, Rishabh V.
and
Ardekani, Arezoo M.
2020.
Effect of roughness on the rheology of concentrated non-Brownian suspensions: A numerical study.
Journal of Rheology,
Vol. 64,
Issue. 1,
p.
67.
Madec, Christopher
Collin, Brivaël
John Soundar Jerome, J.
and
Joubaud, Sylvain
2020.
Puzzling Bubble Rise Speed Increase in Dense Granular Suspensions.
Physical Review Letters,
Vol. 125,
Issue. 7,
More, R. V.
and
Ardekani, A. M.
2020.
Roughness induced shear thickening in frictional non-Brownian suspensions: A numerical study.
Journal of Rheology,
Vol. 64,
Issue. 2,
p.
283.
Octau, C.
Dbouk, T.
Watremez, M.
Meresse, D.
Lippert, M.
Schiffler, J.
Keirsbulck, L.
and
Dubar, L.
2020.
Liquid–solid two-phase jet in a turbulent crossflow: Experiments and simulations.
Chemical Engineering Research and Design,
Vol. 155,
Issue. ,
p.
156.
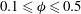 $0.1\leqslant {\it\phi}\leqslant 0.5$. The wall region shows particle layers with a hexagonal structure. The size of this layered zone depends on volume fraction and is only weakly affected by friction. This structure implies a wall slip which is in good accordance with empirical models. Simulations show that this wall slip can be mitigated by reducing particle roughness. For
$0.1\leqslant {\it\phi}\leqslant 0.5$. The wall region shows particle layers with a hexagonal structure. The size of this layered zone depends on volume fraction and is only weakly affected by friction. This structure implies a wall slip which is in good accordance with empirical models. Simulations show that this wall slip can be mitigated by reducing particle roughness. For 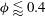 ${\it\phi}\lessapprox 0.4$, wall-induced layering has a moderate impact on the viscosity and second normal stress difference
${\it\phi}\lessapprox 0.4$, wall-induced layering has a moderate impact on the viscosity and second normal stress difference 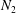 $N_{2}$. Conversely, it significantly alters the first normal stress difference
$N_{2}$. Conversely, it significantly alters the first normal stress difference 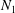 $N_{1}$ and can result in positive
$N_{1}$ and can result in positive 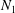 $N_{1}$, in better agreement with some experiments. Friction enhances this effect, which is shown to be due to a substantial decrease in the contact normal stress
$N_{1}$, in better agreement with some experiments. Friction enhances this effect, which is shown to be due to a substantial decrease in the contact normal stress 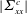 $|{\it\Sigma}_{xx}^{c}|$ (where
$|{\it\Sigma}_{xx}^{c}|$ (where  $x$ is the velocity direction) because of particle layering in the wall region.
$x$ is the velocity direction) because of particle layering in the wall region.