Hostname: page-component-cd9895bd7-dzt6s Total loading time: 0 Render date: 2024-12-28T11:58:22.617Z Has data issue: false hasContentIssue false
  • English
  • Français

The effect of compressibility on the stability of wall-bounded Kolmogorov flow

Published online by Cambridge University Press:  31 January 2012

A. Manela  and
J. Zhang
A. Manela
Affiliation:
Faculty of Aerospace Engineering, Technion, Israel Institute of Technology, Haifa 32000, Israel
J. Zhang*
Affiliation:
Laboratory of High Temperature Gas Dynamics, Institute of Mechanics, Chinese Academy of Sciences, Beijing 100190, China
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We extend the stability analysis of incompressible Kolmogorov flow, induced by a spatially periodic external force in an unbounded domain, to a compressible hard-sphere gas confined between two parallel isothermal walls. The two-dimensional problem is studied by means of temporal stability analysis of a ‘slip flow’ continuum-limit model and the direct simulation Monte Carlo (DSMC) method. 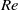The neutral curve is obtained in terms of the Reynolds () and Knudsen (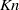) numbers, for a given non-dimensional wavenumber 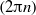of the external force. In the incompressible limit (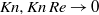), the problem is governed only by the Reynolds number, and our neutral curve coincides with the critical Reynolds number (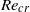) calculated in previous incompressible analyses. Fluid compressibility (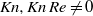) affects the flow field through the generation of viscous dissipation, coupling flow shear rates with irreversible heat production, and resulting in elevated bulk-fluid temperatures. This mechanism has a stabilizing effect on the system, thus increasing (compared to its incompressible value) with increasing 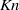. When compressibility effects become strong enough, transition to instability changes type from ‘exchange of stabilities’ to ‘overstability’, and perturbations are dominated by fluctuations in the thermodynamic fields. Most remarkably, compressibility confines the instability to small (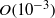) Knudsen numbers, above which the Kolmogorov flow is stable for all 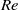. Good agreement is found between ‘slip flow’ and DSMC analyses, suggesting the former as a useful alternative in studying the effects of various parameters on the onset of instability, particularly in the context of small Knudsen numbers considered.

JFM classification

Compressible Flows: Gas dynamics Instability: Instability Rarefied Gas Flow: Rarefied Gas Flow
Type
Papers
Information
Journal of Fluid Mechanics , Volume 694 , 10 March 2012 , pp. 29 - 49
Copyright
Copyright © Cambridge University Press 2012

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1. Arnol’d, V. I. & Meshalkin, L. D. 1960 A. N. Kolmogorov’s seminar on selected problems of analysis (1958/1959). Usp. Mat. Nauk 15, 247–250 (in Russian).Google Scholar
2. Bena, I., Malek Mansour, M. & Baras, F. 1999 Hydrodynamic fluctuations in the Kolmogorov flow: linear regime. Phys. Rev. E 59, 5503–5510.CrossRefGoogle ScholarPubMed
3. Bird, G. 1994 Molecular Gas Dynamics and the Direct Simulations of Gas Flows. Clarendon Press.CrossRefGoogle Scholar
4. Burgess, J. M., Bizon, C., McCormick, W. D., Swift, J. B. & Swinney, H. L. 1999 Instability of the Kolmogorov flow in a soap film. Phys. Rev. E 60, 715–721.CrossRefGoogle Scholar
5. Chandrasekhar, S. 1961 Hydrodynamic and Hydromagnetic Stability. Clarendon Press.Google Scholar
6. Fukuta, H. & Murakami, Y. 1998 Side-wall effect on the long-wave instability in Kolmogorov flow. J. Phys. Soc. Japan 67, 1597–1602.CrossRefGoogle Scholar
7. Golshtein, E. & Elperin, T. 1996 Convective instabilities in rarefied gases by direct simulation Monte Carlo method. J. Thermophys. Heat Transfer 10, 250–256.CrossRefGoogle Scholar
8. Green, J. S. A. 1974 Two-dimensional turbulence near the viscous limit. J. Fluid Mech. 62, 273–287.CrossRefGoogle Scholar
9. von Kármán, T. 1963 From Low-Speed Aerodynamics to Astronautics. Pergamon Press.Google Scholar
10. Manela, A. & Frankel, I. 2005 On the Rayleigh–Bénard problem in the continuum limit. Phys. Fluids 17, 036101.CrossRefGoogle Scholar
11. Manela, A. & Frankel, I. 2007 On the compressible Taylor–Couette problem. J. Fluid Mech. 588, 59–74.CrossRefGoogle Scholar
12. Meshalkin, L. D. & Sinai, Ia. G. 1961 Investigation of the stability of a stationary solution of a system of equations for the plane movement of an incompressible viscous fluid. Prikl. Mat. Mekh. 25, 1140–1143.Google Scholar
13. Peyret, R. 2002 Spectral Methods for Incompressible Viscous Flow. Springer.CrossRefGoogle Scholar
14. Platt, N., Sirovich, L. & Fitzmaurice, N. 1991 An investigation of chaotic Kolmogorov flows. Phys. Fluids A 3, 681–696.CrossRefGoogle Scholar
15. She, Z. S. 1987 Metastability and vortex pairing in the Kolmogorov flow. Phys. Lett. A 124, 161–164.CrossRefGoogle Scholar
16. Sivashinsky, A. 1985 Weak turbulence in periodic flows. Physica D 17, 243–255.CrossRefGoogle Scholar
17. Sommeria, J. 1986 Experimental study of the two-dimensional inverse energy cascade in a square box. J. Fluid Mech. 170, 139.CrossRefGoogle Scholar
18. Sone, Y. 2002 Kinetic Theory and Fluid Dynamics. Birkhauser.CrossRefGoogle Scholar
19. Squire, H. B. 1933 On the stability for three-dimensional disturbances of viscous fluid flow between parallel walls. Proc. R. Soc. A142, 621–628.Google Scholar
20. Stefanov, S. & Cercignani, C. 1993 Monte Carlo simulation of the Taylor–Couette flow of a rarefied gas. J. Fluid Mech. 256, 199–213.CrossRefGoogle Scholar
21. Stefanov, S., Roussinov, V. & Cercignani, C. 2002 Rayleigh–Bénard flow of a rarefied gas and its attractors. I. Convection regime. Phys. Fluids 14, 2255–2269.CrossRefGoogle Scholar
22. Stefanov, S., Roussinov, V. & Cercignani, C. 2007 Rayleigh–Bénard flow of a rarefied gas and its attractors. III. Three-dimensional computer simulations. Phys. Fluids 19, 124101.CrossRefGoogle Scholar
23. Tabeling, P., Perrin, B. & Fauve, S. 1987 Instability of a linear array of forced vortices. Europhys. Lett. 3, 459–465.CrossRefGoogle Scholar
24. Thess, A. 1992 Instabilities in two-dimensional spatially periodic flows. Part I. Kolmogorov flow. Phys. Fluids A 4, 1385–1395.CrossRefGoogle Scholar
25. Tsien, H. S. 1946 Similarity laws of hypersonic flows. J. Math Phys. 25, 247–252.CrossRefGoogle Scholar
26. Yoshida, H. & Aoki, K. 2006 Linear stability of the cylindrical Couette flow of a rarefied gas. Phys. Rev. E 73, 021201.CrossRefGoogle ScholarPubMed
27. Zhang, J. & Fan, J. 2009 Monte Carlo simulation of thermal fluctuations below the onset of Rayleigh–Bénard convection. Phys. Rev. E 79, 056302.CrossRefGoogle ScholarPubMed
28. Zhang, J. & Fan, J. 2011 Monte Carlo Simulation of two-dimensional Kolmogorov flow. In Rarefied Gas Dynamics (ed. Levin, D. A., Wysong, I. J. & Garcia, A. L. ), pp. 378–383. American Institute of Physics.Google Scholar