Hostname: page-component-745bb68f8f-l4dxg Total loading time: 0 Render date: 2025-02-11T11:47:29.389Z Has data issue: false hasContentIssue false
  • English
  • Français

The effect of a non-zero Lagrangian time scale on bounded shear dispersion

Published online by Cambridge University Press:  13 December 2011

Matthew S. Spydell  and
Falk Feddersen
Matthew S. Spydell*
Affiliation:
Integrative Oceanography Division, Scripps Institution of Oceanography, La Jolla, CA 92093-0209, USA
Falk Feddersen
Affiliation:
Integrative Oceanography Division, Scripps Institution of Oceanography, La Jolla, CA 92093-0209, USA
*
†Email address for correspondence: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Previous studies of shear dispersion in bounded velocity fields have assumed random velocities with zero Lagrangian time scale (i.e. velocities are 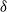-function correlated in time). However, many turbulent (geophysical and engineering) flows with mean velocity shear exist where the Lagrangian time scale is non-zero. Here, the longitudinal (along-flow) shear-induced diffusivity in a two-dimensional bounded velocity field is derived for random velocities with non-zero Lagrangian time scale 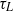. A non-zero 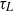results in two-time transverse (across-flow) displacements that are correlated even for large (relative to the diffusive time scale 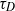) times. The longitudinal (along-flow) shear-induced diffusivity 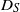is derived, accurate for all 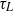, using a Lagrangian method where the velocity field is periodically extended to infinity so that unbounded transverse particle spreading statistics can be used to determine 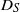. The non-dimensionalized 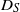depends on time and two parameters: the ratio of Lagrangian to diffusive time scales 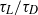and the release location. Using a parabolic velocity profile, these dependencies are explored numerically and through asymptotic analysis. The large-time 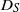is enhanced relative to the classic Taylor diffusivity, and this enhancement increases with 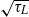. At moderate 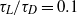this enhancement is approximately a factor of 3. For classic shear dispersion with 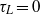, the diffusive time scale 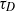determines the time dependence and large-time limit of the shear-induced diffusivity. In contrast, for sufficiently large 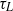, a shear time scale 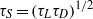, anticipated by a simple analysis of the particle’s domain-crossing time, determines both the 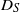time dependence and the large-time limit. In addition, the scalings for turbulent shear dispersion are recovered from the large-time 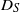using properties of wall-bounded turbulence.

JFM classification

Mixing: Mixing
Type
Papers
Information
Journal of Fluid Mechanics , Volume 691 , 25 January 2012 , pp. 69 - 94
Copyright
Copyright © Cambridge University Press 2011 The online version of this article is published within an Open Access environment subject to the conditions of the Creative Commons Attribution-NonCommercial-ShareAlike licence <http://creativecommons.org/licenses/by-nc-sa/2.5/>. The written permission of Cambridge University Press must be obtained for commercial re-use.

References

1. Aris, R. 1956 On the dispersion of a solute in a fluid flowing through a tube. Proc. R. Soc. Lond. A 235, 67–77.Google Scholar
2. Barton, N. 1983 On the method of moments for solute dispersion. J. Fluid Mech. 126, 205–218.CrossRefGoogle Scholar
3. Berloff, P. S. & McWilliams, J. C. 2002 Material transport in oceanic gyres. Part II: hierarchy of stochastic models. J. Phys. Ocean. 32 (3), 797–830.2.0.CO;2>CrossRefGoogle Scholar
4. Camassa, R., Lin, Z. & McLaughlin, R. M. 2010 The exact evolution of the scalar variance in pipe and channel flow. Commun. Math. Sci. 8, 601–626.CrossRefGoogle Scholar
5. Castiglione, P. & Crisanti, A. 1999 Dispersion of passive tracers in a velocity field with non-delta-correlated noise. Phys. Rev. E 59, 3926–3934.CrossRefGoogle Scholar
6. Davis, R. E. 1985 Drifter observation of coastal currents during CODE: the statistical and dynamical perspective. J. Geophys. Res. 90, 4756–4772.CrossRefGoogle Scholar
7. Dever, E. P., Hendershott, M. C. & Winant, C. D. 1998 Statistical aspects of surface drifter observations of circulation in the Santa Barbara Channel. J. Geophys. Res. 103, 24,781–24,797.CrossRefGoogle Scholar
8. Dewey, R. J. & Sullivan, P. J. 1982 Longitudinal-dispersion calculations in laminar flows by statistical analysis of molecular motions. J. Fluid Mech. 125, 203–218.CrossRefGoogle Scholar
9. Elder, J. W. 1959 The dispersion of marked fluid in turbulent shear flow. J. Fluid Mech. 5, 544–560.CrossRefGoogle Scholar
10. Haber, S. & Mauri, R. 1988 Lagrangian approach to time-dependent laminar dispersion in rectangular conduits. Part 1. Two-dimensional flows. J. Fluid Mech. 190, 201–215.CrossRefGoogle Scholar
11. Katayama, Y. & Terauti, R. 1996 Brownian motion of a single particle under shear flow. Eur. J. Phys. 17, 136–140.CrossRefGoogle Scholar
12. Latini, M. & Bernoff, A. J. 2001 Transient anomalous diffusion in Poiseuille flow. J. Fluid Mech. 441, 399–411.CrossRefGoogle Scholar
13. Li, T., Kheifets, S., Medellin, D. & Raizen, M. G. 2010 Measurement of the instantaneous velocity of a Brownian particle. Science 328 (5986), 1673–1675.CrossRefGoogle ScholarPubMed
14. McClean, J. L., Poulain, P. M. & Pelton, J. W. 2002 Eulerian and Lagrangian statistics from surface drifters and a high-resolution POP simulation in the North Atlantic. J. Phys. Oceanogr. 32, 2472–2491.CrossRefGoogle Scholar
15. Pavliotis, G. A. & Stuart, A. M. 2005 Periodic homogenization for inertial particles. Physica D 204, 161–187.CrossRefGoogle Scholar
16. Pavliotis, G., Stuart, A. M. & Zygalakis, K. 2007 Homogenization for inertial particles in a random flow. Commun. Math. Sci. 5, 507–531.CrossRefGoogle Scholar
17. Pavliotis, G. A., Stuart, A. M. & Zygalakis, K. C. 2009 Calculating effective diffusivities in the limit of vanishing molecular diffusion. J. Comput. Phys. 228, 1030–1055.CrossRefGoogle Scholar
18. Sallée, J. B., Speer, K., Morrow, R. & Lumpkin, R. 2008 An estimate of Lagrangian eddy statistics and diffusion in the mixed layer of the Southern Ocean. J. Mar. Res. 66 (4), 441–463.CrossRefGoogle Scholar
19. Sawford, B. L. & Yeung, P. K. 2001 Lagrangian statistics in uniform shear flow: direct numerical simulation and Lagrangian stochastic models. Phys. Fluids 13 (9), 2627–2634.CrossRefGoogle Scholar
20. Spydell, M., Feddersen, F. & Guza, R. T. 2009 Observations of drifter dispersion in the surfzone: the effect of sheared alongshore currents. J. Geophys. Res. 114.Google Scholar
21. Taylor, G. I. 1922 Diffusion by continuous movements. Proc. Lond. Math. Soc. 20, 196–212.CrossRefGoogle Scholar
22. Taylor, G. I. 1953 Dispersion of soluble matter in solvent flowing slowly through a tube. Proc. Roy. Soc. A 219, 186–203.Google Scholar
23. Taylor, G. I. 1954 The dispersion of matter in turbulent flow through a pipe. Proc. Roy. Soc. A 223, 446–468.Google Scholar
24. Tennekes, H. & Lumley, J. L. 1972 A First Course in Turbulence. MIT Press.CrossRefGoogle Scholar
25. Uhlenbeck, G. E. & Ornstein, L. S. 1930 On the theory of the Brownian motion. Phys. Rev. 36, 823–841.CrossRefGoogle Scholar
26. Van Den Broeck, C. 1982 A stochastic description of longitudinal dispersion in uniaxial flows. Physica A 112A, 343–352.CrossRefGoogle Scholar
27. Wilson, J. D. & Sawford, B. L. 1996 Review of Lagrangian stochastic models for trajectories in the turbulent atmosphere. Boundary-Layer Meteorol. 78 (1), 191–210.CrossRefGoogle Scholar
28. Young, W. R. & Jones, S. 1991 Shear dispersion. Phys. Fluids A 3 (5), 1087–1101.CrossRefGoogle Scholar
29. Zambianchi, E. & Griffa, A. 1994 Effects of finite scales of turbulence on dispersion estimates. J. Mar. Res. 52, 129–148.CrossRefGoogle Scholar
30. Zhurbas, V. 2003 Lateral diffusivity and Lagrangian scales in the Pacific Ocean as derived from drifter data. J. Geophys. Res. 108 (C5).Google Scholar