Hostname: page-component-cd9895bd7-dk4vv Total loading time: 0 Render date: 2024-12-28T22:12:25.703Z Has data issue: false hasContentIssue false
  • English
  • Français

Early-time periodic injection and extraction in an inclined confined aquifer

Published online by Cambridge University Press:  10 July 2015

Peter Dudfield  and
Andrew W. Woods
Peter Dudfield*
Affiliation:
BP Institute, University of Cambridge, Madingley Rise, Madingley Road, Cambridge CB3 0EZ, UK
Andrew W. Woods
Affiliation:
BP Institute, University of Cambridge, Madingley Rise, Madingley Road, Cambridge CB3 0EZ, UK
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We consider the periodic injection and extraction of fluid from a horizontal line well in an inclined saturated aquifer of finite thickness, 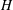$H$, as part of an aquifer thermal energy storage system. We focus on the case in which the injected fluid is dense relative to the original fluid in the aquifer and hence tends to run off downslope, so that during the extraction cycle a mixture of original aquifer fluid and injected fluid is produced. We study the controls on the composition of the extracted fluid, distinguishing between the cases where there is an open boundary downslope or upslope of the source, with the other boundary being sealed. We find that initially the fraction of original aquifer fluid recovered during an extracted cycle decreases from cycle to cycle, and at long times this fraction asymptotes to a value, 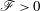$\mathscr{F}>0$, that depends on 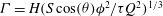${\it\Gamma}=H(S\cos ({\it\theta}){\it\phi}^{2}/{\it\tau}Q^{2})^{1/3}$ and 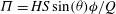${\it\Pi}=HS\sin ({\it\theta}){\it\phi}/Q$, where ${\it\tau}$ is the time period of injection, 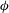${\it\phi}$ is the porosity of the aquifer, 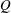$Q$ is the injection rate, 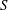$S$ is the speed of the buoyancy driven flow and 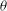${\it\theta}$ is the angle of inclination to the horizontal. At long times the flow asymptotes to a quasi-steady exchange flow solution that develops in an inclined saturated porous layer of thickness 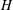$H$ in contact with a stratified fluid reservoir, filled to thickness 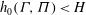$h_{0}({\it\Gamma},{\it\Pi})<H$ with relatively dense fluid. This enables us to calculate the average composition of the extracted fluid, which is of concern if the original aquifer fluid contains contaminants. Since the produced aquifer fluid is driven by this quasi-steady exchange flow, we show that contaminants downslope of the well will be produced after a finite time, whereas contaminants upslope of the well typically remain in the aquifer, irrespective of the far-field boundary conditions. We successfully test the models with a series of analogue experiments of both the injection extraction flow and the exchange flow using a Hele-Shaw cell.

JFM classification

Geophysical and Geological Flows: Gravity currents Low-Reynolds-number flows: Porous media
Type
Papers
Information
Journal of Fluid Mechanics , Volume 776 , 10 August 2015 , pp. 430 - 457
Check for updates
Copyright
© 2015 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Ames, W. F. 1965 Nonlinear Partial Differential Equations in Engineering. Academic Press.Google Scholar
Bakema, G., Snijders, A. & Nordell, B (Programme, IEA Energy Storage) 1994 Underground Thermal Energy Storage: State of the Art 1994. IF Technology bv, Arnhem.Google Scholar
Barenblatt, G. I., Entov, V. M. & Ryzhik, V. M. 1990 Theory of Fluid Flows through Natural Rocks. Kluwer.Google Scholar
Bear, J. 1988 Dynamics of Fluids in Porous Media. Dover.Google Scholar
Bear, J. & Cheng, A. D. 2010 Modeling Groundwater Flow and Contaminant Transport. Springer Science and Business Media.CrossRefGoogle Scholar
Dickinson, J. S., Buik, N., Matthews, M. C. & Snijders, A. 2009 Aquifer thermal energy storage: theoretical and operational analysis. Géotechnique 59 (3), 249–260.Google Scholar
Dudfield, P. & Woods, A. W. 2012 On the periodic injection of fluid into, and its extraction from, a porous medium for seasonal heat storage. J. Fluid Mech. 707, 467–481.Google Scholar
Dudfield, P. & Woods, A. W. 2014 On the periodic injection of fluid into, and its extraction from, a confined aquifer. J. Fluid Mech. 755, 111–141.CrossRefGoogle Scholar
Eichel, H., Helmig, R., Neuweiler, I. & Cirpka, O. A. 2005 Upscaling of two-phase flow processes in porous media. In Upscaling Multiphase Flow in Porous Media (ed. Das, D. B. & Hassanizadeh, S. M.), pp. 237–257. Springer.Google Scholar
Farcas, A. & Woods, A. W. 2015 Buoyancy-driven dispersion in a layered porous rock. J. Fluid Mech. 767, 226–239.Google Scholar
Gelhar, L. W., Welty, C. & Rehfeldt, K. R. 1992 Review of data on field-scale dispersion in aquifers based on fractal concepts. Water Resour. Res. 28 (7), 1955–1974.Google Scholar
Gringarten, A. C. &  Sauty, J. P. 1975 A theoretical study of heat extraction from aquifers with uniform regional flow. J. Geophys. Res. 80 (35), 4956–4962.Google Scholar
Gunn, I. & Woods, A. W. 2011 On the flow of buoyant fluid injected into a confined, inclined aquifer. J. Fluid Mech. 672, 109–129.Google Scholar
Hesse, M. A., Tchelepi, H. A. & Orr, F. M. 2008 Gravity currents with residual trapping. J. Fluid Mech. 611, 35–60.Google Scholar
Hunt, J. R., Sitar, N. & Udell, K. S. 1988a Nonaqueous phase liquid transport and cleanup: 1. Analysis of mechanisms. Water Resour. Res. 24 (8), 1247–1258.Google Scholar
Hunt, J. R., Sitar, N. & Udell, K. S. 1988b Nonaqueous phase liquid transport and cleanup: 2. Experimental studies. Water Resour. Res. 24 (8), 1259–1269.Google Scholar
Huppert, H. E. & Woods, A. W. 1995 Gravity-driven flows in porous layers. J. Fluid Mech. 292, 55–69.Google Scholar
Lide, D. R. 2001 CRC Handbook of Chemistry and Physics, 82nd edn. CRC Press.Google Scholar
Mackay, D. J. C. 2008 Sustainable Energy – Without the Hot Air. UIT Cambridge.Google Scholar
Neufeld, J. A. & Huppert, H. E. 2009 Modelling carbon dioxide sequestration in layered strata. J. Fluid Mech. 625, 353–370.Google Scholar
Neufeld, J. A., Vella, D. & Huppert, H. E. 2009 The effect of a fissure on storage in a porous medium. J. Fluid Mech. 639, 239–259.CrossRefGoogle Scholar
Sauty, J. P., Gringarten, A. C., Fabris, H., Thiery, D., Menjoz, A. & Landel, P. A. 1982a Sensible energy storage in aquifers: 2. Field experiments and comparison with theoretical results. Water Resour. Res. 18, 253–265.Google Scholar
Sauty, J. P., Gringarten, A. C., Menjoz, A. & Landel, P. A. 1982b Sensible energy storage in aquifers: 1. Theoretical study. Water Resour. Res. 18, 245–252.Google Scholar
Szulczewski, M. L. & Juanes, R. 2013 The evolution of miscible gravity currents in horizontal porous layers. J. Fluid Mech. 719, 82–96.Google Scholar
Vanhoudt, D., Desmedt, J., Van Bael, J., Robeyn, N. & Hoes, H. 2011 An aquifer thermal storage system in a Belgian hospital: long-term experimental evaluation of energy and cost savings. Energy Build. 43 (12), 3657–3665.Google Scholar
Woods, A. W. 2015 Flow in Porous Rocks. Cambridge University Press.Google Scholar
Woods, A. W. &  Mason, R. 2000 The dynamics of two-layer gravity-driven flows in permeable rock. J. Fluid Mech. 421, 83–114.CrossRefGoogle Scholar