Hostname: page-component-78c5997874-8bhkd Total loading time: 0 Render date: 2024-11-04T22:00:15.874Z Has data issue: false hasContentIssue false
  • English
  • Français

Early transition, relaminarization and drag reduction in the flow of polymer solutions through microtubes

Published online by Cambridge University Press:  10 January 2020

Bidhan Chandra ,
V. Shankar Open the ORCID record for V. Shankar [Opens in a new window]  and
Debopam Das Open the ORCID record for Debopam Das [Opens in a new window]
Bidhan Chandra
Affiliation:
Department of Chemical Engineering, Indian Institute of Technology, Kanpur, 208016, India
V. Shankar*
Affiliation:
Department of Chemical Engineering, Indian Institute of Technology, Kanpur, 208016, India
Debopam Das
Affiliation:
Department of Aerospace Engineering, Indian Institute of Technology, Kanpur, 208016, India
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

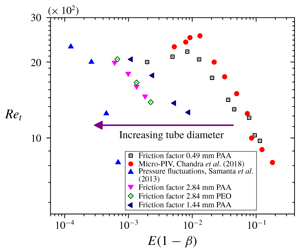
Experiments are performed to investigate the onset of early transition and drag reduction in the flow of polymer (polyacrylamide and polyethylene oxide) solutions through rigid microtubes of diameters in the range 0.49–2.84 mm. We measure friction factor variation with Reynolds number for varying polymer concentrations and tube diameters, and the Reynolds number, $Re_{t}$, at which the experimental data deviate from the laminar value represents the onset of transition. Crucially, owing to the high shear rates encountered in our experiments, we show that it is important to account for shear thinning of the fluid in the theoretical estimation of the friction factor in the laminar regime. We accomplish this using a Carreau model, and show that the use of laminar friction factor calculated without shear thinning leads to an erroneous overestimation of $Re_{t}$. The $Re_{t}$ obtained from friction factor data in the present study is in good agreement with that inferred using micro particle image velocimetry analysis in Chandra et al. (J. Fluid Mech., vol. 844, 2018, pp. 1052–1083). For smaller concentrations of the added polymer, there is a marginal delay in the onset of turbulence, but as the concentration is increased further, the transition Reynolds number decreases much below $2000$, the usual value at which transition occurs in Newtonian pipe flows. Thus, the present study further corroborates the phenomenon of early transition leading to an ‘elasto-inertial’ turbulent state in the flow of polymer solutions. For concentrations such that there is a delay in transition, if $Re$ is maintained above the $Re_{t}$ for Newtonian fluids, the flow is transitional or turbulent in the absence of polymers. At such a fixed $Re$, if the concentration of the polymer is increased gradually, the friction factor decreases and the flow relaminarizes. With further increase in polymer concentration, the flow undergoes a transition due to elasto-inertial instability. The effect of addition of small amounts of polymer on turbulent drag reduction in the flow of water through microtubes is also investigated. Increase in polymer concentration, molecular weight and decrease in tube diameter causes an increase in drag reduction. The friction factor data for different polymer concentrations, molecular weights, tube diameters and $Re$, when plotted with $Wi(1-\unicode[STIX]{x1D6FD})$, show a reasonable collapse, where $Wi$ is the Weissenberg number defined as the product of the longest relaxation time of the polymer solution and the average shear rate in the tube and $\unicode[STIX]{x1D6FD}$ is the ratio of solvent to total solution viscosity. Interestingly, the onset of the maximum drag reduction asymptote, for experiments using varying tube diameters and polymer concentrations, appears to occur at $Wi(1-\unicode[STIX]{x1D6FD})\sim O(1)$.

JFM classification

Non-Newtonian Flows: Viscoelasticity Non-Newtonian Flows: Polymers Instability: Transition to turbulence
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 885 , 25 February 2020 , A47
Copyright
© The Author(s), 2020. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Bodiguel, H., Beaumont, J., Machado, A., Martinie, L., Kellay, H. & Colin, A. 2015 Flow enhancement due to elastic turbulence in channel flows of shear thinning fluids. Phys. Rev. Lett. 114, 028302.CrossRefGoogle ScholarPubMed
Bonn, D., Ingremeau, F., Amarouchene, Y. & Kellay, H. 2011 Large velocity fluctuations in small-Reynolds-number pipe flow of polymer solutions. Phys. Rev. E 84, 045301.Google ScholarPubMed
Chandra, B., Shankar, V. & Das, D. 2018 Onset of transition in the flow of polymer solutions through microtubes. J. Fluid Mech. 844, 1052–1083.CrossRefGoogle Scholar
Choueiri, G. H., Lopez, J. M. & Hof, B. 2018 Exceeding the asymptotic limit of polymer drag reduction. Phys. Rev. Lett. 120, 124501.CrossRefGoogle ScholarPubMed
Dinic, J., Zhang, Y., Jimenez, L. N. & Sharma, V. 2015 Extensional relaxation times of dilute, aqueous polymer solutions. ACS Macro Lett. 4, 804–808.CrossRefGoogle Scholar
Draad, A. A., Kuiken, G. D. C. & Nieuwstadt, F. T. M. 1998 Laminar turbulent transition in pipe flow for Newtonian and non-Newtonian fluids. J. Fluid Mech. 377, 267–312.CrossRefGoogle Scholar
Drazin, P. G. & Reid, W. H. 1981 Hydrodynamic Stability. Cambridge University Press.Google Scholar
Dubief, Y., Terrapon, V. E. & Soria, J. 2013 On the mechanism of elasto-inertial turbulence. Phys. Fluids 25 (11), 110817.CrossRefGoogle ScholarPubMed
Eckhardt, B., Schneider, T. M., Hof, B. & Westerweel, J. 2007 Turbulence transition in pipe flow. Annu. Rev. Fluid Mech. 39 (1), 447–468.CrossRefGoogle Scholar
Escudier, M. P., Nickson, A. K. & Poole, R. J. 2009 Turbulent flow of viscoelastic shear-thinning liquids through a rectangular duct: quantification of turbulence anisotropy. J. Non-Newtonian Fluid Mech. 160 (1), 2–10.CrossRefGoogle Scholar
Escudier, M. P., Poole, R. J., Presti, F., Dales, C., Nouar, C., Desaubry, C., Graham, L. & Pullum, L. 2005 Observations of asymmetrical flow behaviour in transitional pipe flow of yield-stress and other shear-thinning liquids. J. Non-Newtonian Fluid Mech. 127 (2), 143–155.CrossRefGoogle Scholar
Forame, P. C., Hansen, R. J. & Little, R. C. 1972 Observations of early turbulence in the pipe flow of drag reducing polymer solutions. AIChE J. 18 (1), 213–217.CrossRefGoogle Scholar
Garg, P., Chaudhary, I., Khalid, M., Shankar, V. & Subramanian, G. 2018 Viscoelastic pipe flow is linearly unstable. Phys. Rev. Lett. 121, 024502.CrossRefGoogle ScholarPubMed
Gasljevic, K., Aguilar, G. & Matthys, E. F. 1999 An improved diameter scaling correlation for turbulent flow of drag-reducing polymer solutions. J. Non-Newtonian Fluid Mech. 84 (2), 131–148.CrossRefGoogle Scholar
Gasljevic, K., Aguilar, G. & Matthys, E. F. 2001 On two distinct types of drag-reducing fluids, diameter scaling, and turbulent profiles. J. Non-Newtonian Fluid Mech. 96, 405–425.CrossRefGoogle Scholar
Graham, M. D. 2004 Drag reduction in turbulent flow of polymer solutions. Rheol. Rev. 2, 143–170.Google Scholar
Graham, M. D. 2014 Drag reduction and the dynamics of turbulence in simple and complex fluids. Phys. Fluids 26, 101301.CrossRefGoogle Scholar
Hansen, R. J., Little, R. C. & Forame, P. G. 1973 Experimental and theoretical studies of early turbulence. J. Chem. Engng Japan 6 (4), 310–314.CrossRefGoogle Scholar
Hinch, E. J. 1977 Mechanical models of dilute polymer solutions in strong flows. Phys. Fluids 20 (10), S22–S30.CrossRefGoogle Scholar
Housiadas, K. D. & Beris, A. N. 2013 On the skin friction coefficient in viscoelastic wall-bounded flows. Intl J. Heat Fluid Flow 42, 49–67.CrossRefGoogle Scholar
Jackson, D. & Launder, B. 2007 Osborne Reynolds and the publication of his papers on turbulent flow. Annu. Rev. Fluid Mech. 39, 19–35.CrossRefGoogle Scholar
Lee, D. H. & Akhavan, R. 2009 Scaling of polymer drag reduction with polymer and flow parameters in turbulent channel flow. In Advances in Turbulence XII (ed. Eckhardt, B.), pp. 359–362. Springer.CrossRefGoogle Scholar
Neelamegam, R. & Shankar, V. 2015 Experimental study of the instability of laminar flow in a tube with deformable walls. Phys. Fluids 27, 043305.CrossRefGoogle Scholar
Oliver, D. R. & Bakhtiyarov, S. I. 1983 Drag reduction in exceptionally dilute polymer solutions. J. Non-Newtonian Fluid Mech. 12 (1), 113–118.CrossRefGoogle Scholar
Owolabi, B. E., Dennis, D. J. C. & Poole, R. J. 2017 Turbulent drag reduction by polymer additives in parallel-shear flows. J. Fluid Mech. 827, R4.CrossRefGoogle Scholar
Pan, L., Morozov, A., Wagner, C. & Arratia, P. E. 2013 Nonlinear elastic instability in channel flows at low Reynolds numbers. Phys. Rev. Lett. 110, 174502.CrossRefGoogle ScholarPubMed
Park, J. T., Mannheimer, R. J., Grimley, T. A. & Morrow, T. B. 1989 Pipe flow measurements of a transparent non-Newtonian slurry. J. Fluids Engng 111 (3), 331–336.CrossRefGoogle Scholar
Poole, R. J. 2016 Elastic instabilities in parallel shear flows of a viscoelastic shear-thinning liquid. Phys. Rev. Fluids 1, 041301.CrossRefGoogle Scholar
Reynolds, O. 1883 An experimental investigation of the circumstances which determine whether the motion of water shall be direct or sinuous, and of the law of resistance in parallel channels. Proc. R. Soc. Lond. 35, 84–99.Google Scholar
Samanta, D., Dubief, Y., Holzner, M., Schäfer, C., Morozov, A. N., Wagner, C. & Hof, B. 2013 Elasto-inertial turbulence. Proc. Natl Acad. Sci. USA 110, 10557–10562.CrossRefGoogle ScholarPubMed
Sharp, K. V. & Adrian, R. J. 2004 Transition from laminar to turbulent flow in liquid filled microtubes. Exp. Fluids 36, 741–747.CrossRefGoogle Scholar
Shekar, A., McMullen, R. M., Wang, S. N., McKeon, B. J. & Graham, M. D. 2019 Critical-layer structures and mechanisms in elastoinertial turbulence. Phys. Rev. Lett. 122, 124503.CrossRefGoogle ScholarPubMed
Sid, S., Terrapon, V. E. & Dubief, Y. 2018 Two-dimensional dynamics of elasto-inertial turbulence and its role in polymer drag reduction. Phys. Rev. F 3, 011301(R).Google Scholar
Sreenivasan, K. R. & White, C. M. 2000 The onset of drag reduction by dilute polymer additives, and the maximum drag reduction asymptote. J. Fluid Mech. 409, 149–164.CrossRefGoogle Scholar
Srinivas, S. S. & Kumaran, V. 2017 Effect of viscoelasticity on the soft-wall transition and turbulence in a microchannel. J. Fluid Mech. 812, 1076–1118.CrossRefGoogle Scholar
Toms, B. 1948 Observation on the flow of linear polymer solutions through straight tubes at large Reynolds numbers. In Proceedings of the 1st International Congress on Rheology, vol. 2, pp. 135–141. North-Holland.Google Scholar
Verma, M. K. S. & Kumaran, V. 2012 A dynamical instability due to fluid wall coupling lowers the transition Reynolds number in the flow through a flexible tube. J. Fluid Mech. 705, 322–347.CrossRefGoogle Scholar
Virk, P. S. 1975 Drag reduction fundamentals. AIChE J. 21, 625–656.CrossRefGoogle Scholar
Virk, P. S., Merrill, E. W., Mickley, H. S., Smith, K. A. & Mollo-Christensen, E. L. 1967 The Toms phenomenon: turbulent pipe flow of dilute polymer solutions. J. Fluid Mech. 30 (2), 305–328.CrossRefGoogle Scholar
Wen, C., Poole, R. J., Willis, A. P. & Dennis, D. J. C. 2017 Experimental evidence of symmetry-breaking supercritical transition in pipe flow of shear-thinning fluids. Phys. Rev. Fluids 2, 031901.CrossRefGoogle Scholar
White, C. M., Somandepalli, V. S. R. & Mungal, M. G. 2004 The turbulence structure of drag-reduced boundary layer flow. Exp. Fluids 36, 62–69.CrossRefGoogle Scholar
White, M. C. & Mungal, M. G. 2008 Mechanics and prediction of turbulent drag reduction with polymer additives. Annu. Rev. Fluid Mech. 40, 235–256.CrossRefGoogle Scholar
Xi, L. & Graham, M. D. 2010 Turbulent drag reduction and multistage transitions in viscoelastic minimal flow units. J. Fluid Mech. 647, 421–452.CrossRefGoogle Scholar
Zakin, J. L., Ni, C. C., Hansen, R. J. & Reischman, M. M. 1977 Laser Doppler velocimetry studies of early turbulence. Phys. Fluids 20 (10), S85–S88.CrossRefGoogle Scholar