Hostname: page-component-745bb68f8f-cphqk Total loading time: 0 Render date: 2025-01-09T19:14:16.115Z Has data issue: false hasContentIssue false
  • English
  • Français

Dynamics of viscous backflow from a model fracture network

Published online by Cambridge University Press:  12 December 2017

Asaf Dana Open the ORCID record for Asaf Dana [Opens in a new window] ,
Zhong Zheng Open the ORCID record for Zhong Zheng [Opens in a new window] ,
Gunnar G. Peng Open the ORCID record for Gunnar G. Peng [Opens in a new window] ,
Howard A. Stone ,
Herbert E. Huppert  and
Guy Z. Ramon Open the ORCID record for Guy Z. Ramon [Opens in a new window]
Asaf Dana
Affiliation:
The Nancy and Stephen Grand Technion Energy Program, and Department of Civil and Environmental Engineering, Technion–Israel Institute of Technology, Haifa 32000, Israel
Zhong Zheng
Affiliation:
Institute of Theoretical Geophysics, Department of Applied Mathematics and Theoretical Physics, University of Cambridge, Centre for Mathematical Sciences, Wilberforce Road, Cambridge CB3 0WA, UK
Gunnar G. Peng
Affiliation:
Institute of Theoretical Geophysics, Department of Applied Mathematics and Theoretical Physics, University of Cambridge, Centre for Mathematical Sciences, Wilberforce Road, Cambridge CB3 0WA, UK
Howard A. Stone
Affiliation:
Department of Mechanical and Aerospace Engineering, Princeton University, Princeton, NJ 08544, USA
Herbert E. Huppert
Affiliation:
Institute of Theoretical Geophysics, Department of Applied Mathematics and Theoretical Physics, University of Cambridge, Centre for Mathematical Sciences, Wilberforce Road, Cambridge CB3 0WA, UK School of Mathematics and Statistics, University of New South Wales, Kensington NSW 2052, Australia Faculty of Science, University of Bristol, Bristol BS2 6BB, UK
Guy Z. Ramon*
Affiliation:
The Nancy and Stephen Grand Technion Energy Program, and Department of Civil and Environmental Engineering, Technion–Israel Institute of Technology, Haifa 32000, Israel
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Hydraulic fracturing for production of oil and gas from shale formations releases fluid waste, by-products that must be managed carefully to avoid significant harm to human health and the environment. These fluids are presumed to result from a variety of fracture relaxation processes, and are commonly referred to as ‘flowback’ and ‘produced water’, depending primarily on the time scale of their appearance. Here, a model is presented for investigating the dynamics of backflows caused by the elastic relaxation of a pre-strained medium, namely a single fracture and two model fracture network systems: a single bifurcated channel and its generalization for $n$ bifurcated fracture generations. Early- and late-time asymptotic solutions are obtained for the model problems and agree well with numerical solutions. In the late-time period, the fracture apertures and backflow rates exhibit a time dependence of 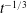$t^{-1/3}$ and 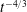$t^{-4/3}$, respectively. In addition, the pressure distributions collapse to universal curves when scaled by the maximum pressure in the system, which we calculate as a function of $n$. The pressure gradient along the network is steepest near the outlet while the bulk of the network serves as a ‘reservoir’. Fracture networks with larger $n$ are less efficient at evicting fluids, manifested through a longer time required for a given fractional reduction of the initial volume. The developed framework may be useful for informing engineering design and environmental regulations.

JFM classification

Low-Reynolds-number flows: Low-Reynolds-number flows Low-Reynolds-number flows: Lubrication theory
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 836 , 10 February 2018 , pp. 828 - 849
Check for updates
Copyright
© 2017 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Batchelor, G. K. 2000 An Introduction to Fluid Dynamics. Cambridge University Press.CrossRefGoogle Scholar
Brown, S. R. 1987 Fluid flow through rock joints: the effect of surface roughness. J. Geophys. Res. 92 (B2), 1337–1347.CrossRefGoogle Scholar
Chau, V. T., Bažant, Z. P. & Su, Y. 2016 Growth model for large branched three-dimensional hydraulic crack system in gas or oil shale. Phil. Trans. R. Soc. Lond. A 374 (2078), 20150418.Google ScholarPubMed
Clarkson, C. R. & Williams-Kovacs, J. 2013 Modeling two-phase flowback of multifractured horizontal wells completed in shale. SPE J. 18, 795–812.CrossRefGoogle Scholar
Ghanbari, E. & Dehghanpour, H. 2016 The fate of fracturing water: a field and simulation study. Fuel 163, 282–294.CrossRefGoogle Scholar
Holditch, S. A. 2007 Hydraulic fracturing: overview, trends, issues. Drilling Contractor 63, 116–118.Google Scholar
Hubbert, M. K. & Willis, D. G. 1972 Mechanics of hydraulic fracturing. Mem.-Am. Assoc. Pet. Geol.; (United States) 18, 239–257.Google Scholar
Kerr, A. D. 1964 Elastic and viscoelastic foundation models. Trans. ASME J. Appl. Mech. 31 (3), 491–498.CrossRefGoogle Scholar
King, G. E. et al. 2010 Thirty years of gas shale fracturing: what have we learned? In SPE Annual Technical Conference and Exhibition. Society of Petroleum Engineers.Google Scholar
Lai, C. Y., Zheng, Z., Dressaire, E., Ramon, G. Z., Huppert, H. E. & Stone, H. A. 2016a Elastic relaxation of fluid-driven cracks and the resulting backflow. Phys. Rev. Lett. 117 (26), 268001.CrossRefGoogle ScholarPubMed
Lai, C. Y., Zheng, Z., Dressaire, E. & Stone, H. A. 2016b Fluid-driven cracks in an elastic matrix in the toughness-dominated limit. Proc. R. Soc. A 374 (2078), 20150425.Google Scholar
Lai, C. Y., Zheng, Z., Dressaire, E., Wexler, J. S. & Stone, H. A. 2015 Experimental study on penny-shaped fluid-driven cracks in an elastic matrix. Proc. R. Soc. A 471 (2182), 20150255.Google Scholar
Landau, L. D. & Lifshitz, E. M. 1986 Theory of Elasticity, 3rd edn. Elsevier.Google Scholar
Lister, J. R. 1990 Buoyancy-driven fluid fracture: the effects of material toughness and of low-viscosity precursors. J. Fluid Mech. 210, 263–280.CrossRefGoogle Scholar
Savitski, A. A. & Detournay, E. 2002 Propagation of a penny-shaped fluid-driven fracture in an impermeable rock: asymptotic solutions. Intl J. Solids Struct. 39 (26), 6311–6337.CrossRefGoogle Scholar
Sone, H. & Zoback, M. D. 2013 Mechanical properties of shale-gas reservoir rocks. Part 1. Static and dynamic elastic properties and anisotropy. Geophysics 78 (5), D381–D392.CrossRefGoogle Scholar
Spence, D. A. & Sharp, P. 1985 Self-similar solutions for elastohydrodynamic cavity flow. Proc. R. Soc. Lond. A 400 (1819), 289–313.Google Scholar
Thompson, M. E. & Brown, S. R. 1991 The effect of anisotropic surface roughness on flow and transport in fractures. J. Geophys. Res. 96 (B13), 21923–21932.CrossRefGoogle Scholar
Zheng, Z., Soh, B., Huppert, H. E. & Stone, H. A. 2013 Fluid drainage from the edge of a porous reservoir. J. Fluid Mech. 718, 558–568.CrossRefGoogle Scholar
Zimmerman, R. W., Kumar, S. & Bodvarsson, G. S. 1991 Lubrication theory analysis of the permeability of rough-walled fractures. In International Journal of Rock Mechanics and Mining Sciences & Geomechanics Abstracts, vol. 28, pp. 325–331. Elsevier.Google Scholar