Hostname: page-component-848d4c4894-jbqgn Total loading time: 0 Render date: 2024-07-07T15:35:57.796Z Has data issue: false hasContentIssue false
  • English
  • Français

Dynamics of unstably stratified free shear flows: an experimental investigation of coupled Kelvin–Helmholtz and Rayleigh–Taylor instability

Published online by Cambridge University Press:  08 March 2017

Bhanesh Akula ,
Prasoon Suchandra ,
Mark Mikhaeil  and
Devesh Ranjan Open the ORCID record for Devesh Ranjan [Opens in a new window]
Bhanesh Akula
Affiliation:
George W. Woodruff School of Mechanical Engineering, Georgia Institute of Technology, 801 Ferst Drive, Atlanta, GA 30332-0405, USA
Prasoon Suchandra
Affiliation:
George W. Woodruff School of Mechanical Engineering, Georgia Institute of Technology, 801 Ferst Drive, Atlanta, GA 30332-0405, USA
Mark Mikhaeil
Affiliation:
George W. Woodruff School of Mechanical Engineering, Georgia Institute of Technology, 801 Ferst Drive, Atlanta, GA 30332-0405, USA
Devesh Ranjan*
Affiliation:
George W. Woodruff School of Mechanical Engineering, Georgia Institute of Technology, 801 Ferst Drive, Atlanta, GA 30332-0405, USA
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

The dynamics of the coupled Kelvin–Helmholtz (KH) and Rayleigh–Taylor (RT) instability (referred to as KHRT instability or KHRTI) is studied using statistically steady experiments performed in a multi-layer gas tunnel. Experiments are performed at four density ratios ranging in Atwood number 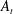$A_{t}$ from 0.035 to 0.159, with varying amounts of shear and 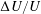$\unicode[STIX]{x0394}U/U$ ranging from 0 to 0.48, where 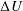$\unicode[STIX]{x0394}U$ is the speed difference between the two flow streams being investigated and 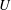$U$ is the mean velocity of these two streams. Three types of diagnostics – back-lit visualization, hot-wire anemometry and particle image velocimetry (PIV) – are employed to obtain the mixing widths, velocity field and density field. The flow is found to be governed by KH dynamics at early times and RT dynamics at late times. This transition from KH-instability-like to RT-instability-like behaviour is quantified using the Richardson number. Transitional Richardson number magnitudes obtained for the present KHRT flows are found to be in the range 0.17–0.56 similar to the critical Richardson numbers for stably stratified free shear flows. Comparing the evolution of density and velocity mixing widths, the density mixing layer is found to be approximately two times as thick as the velocity mixing layer. Scaling of velocity fluctuations is attempted using combinations of KH and RT scales. It is found that the proposed KHRT velocity scale, obtained using the combined mixing-layer growth equation, is appropriate for intermediate stages of the flow when both KH and RT dynamics are comparable. Probability density functions (p.d.f.s) for different fluctuating quantities are presented. Multiple peaks in p.d.f.s are qualitatively explained from the development of coherent KH roll-ups and their subsequent transition into turbulent pockets. The evolution of energy spectra indicates that density fluctuations start to show an inertial subrange from earlier times compared to velocity fluctuations. The spectra exhibit a slightly steeper slope than the Kolmogorov–Obukhov five-thirds law.

JFM classification

Convection: Buoyancy-driven instability Boundary Layers: Free shear layers Geophysical and Geological Flows: Stratified flows
Type
Papers
Information
Journal of Fluid Mechanics , Volume 816 , 10 April 2017 , pp. 619 - 660
Check for updates
Copyright
© 2017 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Abarzhi, S. 2010 On fundamentals of Rayleigh–Taylor turbulent mixing. Europhys. Lett. 91, 35001.Google Scholar
Akula, B.2014 Experimental investigation of buoyancy driven mixing with and without shear at different Atwood numbers. PhD thesis, Texas A&M University.Google Scholar
Akula, B., Andrews, M. J. & Ranjan, D. 2013 Effect of shear on Rayleigh–Taylor mixing at small Atwood number. Phys. Rev. E 87, 033013.Google Scholar
Akula, B. & Ranjan, D. 2016 Dynamics of buoyancy-driven flows at moderately high Atwood numbers. J. Fluid Mech. 795, 313–355.Google Scholar
AMS 2017 Glossary of Meteorology. American Meteorological Society; http://glossary.ametsoc.org/wiki/Citation.Google Scholar
Banerjee, A. & Andrews, M. J. 2006 Statistically steady measurements of Rayleigh–Taylor mixing in a gas channel. Phys. Fluids 18, 035107.Google Scholar
Banerjee, A., Gore, R. A. & Andrews, M. J. 2010a Development and validation of a turbulent-mix model for variable-density and compressible flows. Phys. Rev. E 82, 046309.Google Scholar
Banerjee, A., Kraft, W. N. & Andrews, M. J. 2010b Detailed measurements of a statistically steady Rayleigh–Taylor mixing layer from small to high Atwood numbers. J. Fluid Mech. 659, 127–190.Google Scholar
Batchelor, G. K. 1969 Computation of the energy spectrum in homogeneous two-dimensional turbulence. Phys. Fluids 12, 233–239.Google Scholar
Bell, J. H. & Mehta, R. D. 1990 Development of two-stream mixing layer from tripped and untripped boundary layers. AIAA J. 28, 2034–2042.Google Scholar
Bendat, J. S. & Piersol, A. G. 2010 Random Data: Analysis and Measurement Procedures, 4th edn. Wiley.Google Scholar
Betti, R. & Hurricane, O. A. 2016 Inertial-confinement fusion with lasers. Nat. Phys. 12, 435–448.Google Scholar
Birkhoff, G.1955 Taylor instability and laminar mixing. University of California Report No. LA-1862.Google Scholar
Boffetta, G. & Mazzino, A. 2017 Incompressible Rayleigh–Taylor turbulence. Annu. Rev. Fluid Mech. 49, 119–143.Google Scholar
Bolgiano, R. 1959 Turbulent spectra in a stably stratified atmosphere. J. Geophys. Res. 64 (12), 2226–2229.Google Scholar
Browand, F. K. & Winant, C. D. 1973 Laboratory observations of shear-layer instability in a stratified fluid. Boundary-Layer Meteorol. 5, 67–77.Google Scholar
Brown, G. L. & Roshko, A. 1974 On density effects and large structure in turbulent mixing layers. J. Fluid Mech. 64, 775–816.Google Scholar
Cabot, W. H. & Cook, A. W. 2006 Reynolds number effects on Rayleigh–Taylor instability with possible implications for type-Ia supernovae. Nat. Phys. 2, 562–568.Google Scholar
Champagne, F. H., Pao, Y. H. & Wygnanski, I. J. 1976 On the two-dimensional mixing region. J. Fluid Mech. 74, 209–250.Google Scholar
Chandrasekhar, S. 1961 Hydrodynamic and Hydromagnetic Stability. Oxford University Press.Google Scholar
Cherfils, C. & Mikaelian, K. O. 1996 Simple model for the turbulent mixing width at an ablating surface. Phys. Fluids 8, 522–535.Google Scholar
Cook, A. W., Cabot, W. & Miller, P. L. 2004 The mixing transition in Rayleigh–Taylor instability. J. Fluid Mech. 511, 333–362.Google Scholar
Cook, A. W. & Dimotakis, P. E. 2001 Transition stages of Rayleigh–Taylor instability between miscible fluids. J. Fluid Mech. 443, 69–99.Google Scholar
Davidson, P. A. 2015 Turbulence: An Introduction for Scientists and Engineers, 2nd edn. Oxford University Press.Google Scholar
Dimonte, G. & Schneider, M. 2000 Density ratio dependence of Rayleigh–Taylor mixing for sustained and impulsive acceleration histories. Phys. Fluids 12, 304–321.Google Scholar
Dimotakis, P. E. 1991 Turbulent free shear layer mixing and combustion. High Speed Flight Propulsion Systems 137, 265–340.Google Scholar
Drazin, P. G. & Reid, W. H. 2004 Hydrodynamic Stability. Cambridge University Press.Google Scholar
Fermi, E. & Neumann, J. V.1955 Taylor instability of incompressible liquids. United States Atomic Energy Commission: Unclassified, AECU-2979.Google Scholar
Groeneveld, R. A. & Meeden, G. 1984 Measuring skewness and kurtosis. Statistician 33 (4), 391–399.Google Scholar
Groth, J. & Johansson, A. V. 1988 Turbulence reduction by screens. J. Fluid Mech. 197, 139–155.Google Scholar
Hishida, M. & Nagano, Y. 1978 Simultaneous measurements of velocity and temperature in non isothermal flows. J. Heat Transfer 100, 340–345.Google Scholar
Joanes, D. N. & Gill, C. A. 1998 Comparing measures of sample skewness and kurtosis. J. R. Stat. Soc. D 47 (1), 183–189.Google Scholar
Karimi, M. & Girimaji, S. S. 2016 Suppression mechanism of Kelvin–Helmholtz instability in compressible fluid flows. Phys. Rev. E 93, 041102(R).Google Scholar
Kelley, M. C., Chen, C. Y., Beland, R. R., Woodman, R., Chau, J. L. & Werne, J. 2005 Persistence of a Kelvin–Helmholtz instability complex in the upper troposphere. J. Geophys. Res. 110 (D14), 1–7.Google Scholar
Kolmogorov, A. N. 1941a Dissipation of energy in the locally isotropic turbulence. Proc. USSR Acad. Sci. 32, 16–18.Google Scholar
Kolmogorov, A. N. 1941b The local structure of turbulence in incompressible viscous fluid for very large Reynolds numbers. Proc. USSR Acad. Sci. 30, 299–303.Google Scholar
Kolmogorov, A. N. 1962 A refinement of previous hypotheses concerning the local structure of turbulence in a viscous incompressible fluid at high Reynolds number. J. Fluid Mech. 13, 82–85.Google Scholar
Koop, C. G. & Browand, F. K. 1979 Instability and turbulence in a stratified fluid with shear. J. Fluid Mech. 93, 135–159.Google Scholar
Kraft, W. N.2008 Simultaneous and instantaneous measurement of velocity and density in Rayleigh–Taylor mixing layers. PhD thesis, Texas A&M University.Google Scholar
Kraft, W. N., Banerjee, A. & Andrews, M. J. 2009 On hot-wire diagnostics in Rayleigh–Taylor mixing layers. Exp. Fluids 47, 49–68.Google Scholar
Kraichnan, R. H. 1959 The structure of isotropic turbulence at very high Reynolds numbers. J. Fluid Mech. 5 (4), 497–543.Google Scholar
Kumar, A., Chatterjee, A. G. & Verma, M. K. 2014 Energy spectrum of buoyancy-driven turbulence. Phys. Rev. E 90, 023016.Google Scholar
Lawrence, G. A., Browand, F. K. & Redekopp, L. G. 1991 The stability of a sheared density interface. Phys. Fluids A 3, 2360–2370.Google Scholar
Lewis, D. J. 1950 The instability of liquid surfaces when accelerated in a direction perpendicular to their planes. II. Proc. R. Soc. Lond. A 202, 81–96.Google Scholar
Loehrke, R. I. & Nagib, H. M.1972 Experiments on management of free-stream turbulence. AGARD Report No. 598.Google Scholar
Lohse, D. & Xia, K. Q. 2010 Small-scale properties of turbulent Rayleigh–Bénard convection. Annu. Rev. Fluid Mech. 42, 335–364.Google Scholar
Lyons, R., Panofsky, H. A. & Wollaston, S. 1964 The critical Richardson number and its implications for forecast problems. J. Appl. Meteorol. 3, 136–142.Google Scholar
Mikaelian, K. O. 1989 Turbulent mixing generated by Rayleigh–Taylor and Richtmyer–Meshkov instabilities. Physica D 36, 343–357.Google Scholar
Moran, M. J. & Shapiro, H. N. 2000 Fundamentals of Engineering Thermodynamics. Wiley.Google Scholar
Mueschke, N. J., Andrews, M. J. & Schilling, O. 2006 Experimental characterization of initial conditions and spatio-temporal evolution of a small-Atwood-number Rayleigh–Taylor mixing layer. J. Fluid Mech. 567, 27–63.Google Scholar
Mueschke, N. J. & Schilling, O. 2009a Investigation of Rayleigh–Taylor turbulence and mixing using direct numerical simulation with experimentally measured initial conditions. I. Comparison to experimental data. Phys. Fluids 21, 014106.Google Scholar
Mueschke, N. J. & Schilling, O. 2009b Investigation of Rayleigh–Taylor turbulence and mixing using direct numerical simulation with experimentally measured initial conditions. II. Dynamics of transitional flow and mixing statistics. Phys. Fluids 21, 014107.Google Scholar
Nagata, K. & Komori, S. 2000 The effects of unstable stratification and mean shear on the chemical reaction in grid turbulence. J. Fluid Mech. 408, 39–52.Google Scholar
Obukhov, A. M. 1941 On the spectral energy distribution in a turbulent flow. Izv. Akad. Nauk SSSR Geogr. Geofiz. 5, 453–466.Google Scholar
Obukhov, A. M. 1959 Effect of Archimedean forces on the structure of the temperature field in a turbulent flow. Dokl. Akad. Nauk SSSR 125 (6), 1246–1248.Google Scholar
Obukhov, A. M. 1962 Some specific features of atmospheric turbulence. J. Geophys. Res. 67 (8), 3011–3014.Google Scholar
Olson, B. J., Larsson, J., Lele, S. K. & Cook, A. W. 2011 Nonlinear effects in the combined Rayleigh–Taylor/Kelvin–Helmholtz instability. Phys. Fluids 23, 114107.Google Scholar
Papoulis, A. & Pillai, S. U. 2002 Probability, Random Variables and Stochastic Processes, 4th edn. McGraw-Hill.Google Scholar
Pope, S. B. 2000 Turbulent Flows. Cambridge University Press.Google Scholar
Poujade, O. 2006 Rayleigh–Taylor turbulence is nothing like Kolmogorov turbulence in the self-similar regime. Phys. Rev. Lett. 97, 185002.Google Scholar
Ramaprabhu, P. K. & Andrews, M. J. 2004 Experimental investigation of Rayleigh–Taylor mixing at small Atwood numbers. J. Fluid Mech. 502, 233–271.Google Scholar
Ristorcelli, J. R. & Clark, T. T. 2004 Rayleigh–Taylor turbulence: self-similar analysis and direct numerical simulations. J. Fluid Mech. 507, 213–253.Google Scholar
Schubauer, G. B., Spangenberg, W. G. & Klebanoff, P. S.1950 Aeodynamic characteristics of damping screens. NACA TN 2001.Google Scholar
Sharp, D. H. 1984 An overview of Rayleigh–Taylor instability. Physica D 12, 3–18.Google Scholar
Shumlak, U. & Roderick, N. F. 1998 Mitigation of the Rayleigh–Taylor instability by sheared axial flows. Phys. Plasmas 5, 2384–2389.Google Scholar
Snider, D. M.1994 A study of compound buoyancy and shear mixing. PhD thesis, Texas A&M University.Google Scholar
Snider, D. M. & Andrews, M. J. 1994 Rayleigh–Taylor and shear driven mixing with an unstable thermal stratification. Phys. Fluids 6, 3324–3334.Google Scholar
Snider, D. M. & Andrews, M. J. 1996a The simulation of mixing layers driven by compound buoyancy and shear. Trans. ASME J. Fluids Engng 118, 370–376.Google Scholar
Snider, D. M. & Andrews, M. J. 1996b The structure of shear driven mixing with an unstable thermal stratification. Trans. ASME J. Fluids Engng 118, 55–60.Google Scholar
Sreenivasan, K. R. & Abarzhi, S. I. 2013 Acceleration and turbulence in Rayleigh–Taylor mixing. Phil. Trans. R. Soc. Lond. A 371, 20130267.Google Scholar
de Stadler, M. B., Sarkar, S & Brucker, K. A. 2010 Effect of the Prandtl number on a stratified turbulent wake. Phys. Fluids 22, 095102.Google Scholar
Taylor, G. I. 1931 Effect of variation in density on the stability of superposed streams of fluids. Philos. Trans. R. Soc. Lond. A 246, 499–523.Google Scholar
Taylor, G. I. 1938 The spectrum of turbulence. Proc. R. Soc. Lond. A 164, 476–490.Google Scholar
Tennekes, H. & Lumley, J. L. 1972 A First Course in Turbulence. MIT Press.Google Scholar
Thorpe, S. A. 1968 A method of producing a shear flow in a stratified fluid. J. Fluid Mech. 32, 693–704.Google Scholar
Thorpe, S. A. 1971 Experiments on the instability of stratified shear flows: miscible fluids. J. Fluid Mech. 46, 299–319.Google Scholar
Thorpe, S. A. 1973a Experiments on instability and turbulence in a stratified shear flow. J. Fluid Mech. 61, 731–751.Google Scholar
Thorpe, S. A. 1973b Turbulence in stably stratified fluids: a review of laboratory experiments. Boundary-Layer Meteorol. 5, 95–119.Google Scholar
Townsend, A. A. 1980 The Structure of Turbulent Shear Flow, 2nd edn. Cambridge University Press.Google Scholar
Turner, J. S. 1980 Buoyancy Effects in Fluids. Cambridge University Press.Google Scholar
Vandenboomgaerde, M., Bonnefille, M. & Gauthier, P. 2016 The Kelvin–Helmholtz instability in National Ignition Facility hohlraums as a source of gold-gas mixing. Phys. Plasmas 23 (5), 052704.Google Scholar
Velasco, A. M. & Muñoz, J. D. 2015 Study of hydrodynamic instabilities with a multiphase lattice Boltzmann model. C. R. Méc. 343 (10), 571–579.Google Scholar
Vukoslavc̆ević, P. V., Radulović, I. M. & Wallace, J. M. 2005 Testing of a hot- and cold-wire probe to measure simultaneously the speed and temperature in supercritical CO2 flow. Exp. Fluids 39, 703–711.Google Scholar
Werne, J. & Fritts, D. C. 1999 Stratified shear turbulence: Evolution and statistics. Geophys. Res. Lett. 26 (4), 439–442.Google Scholar
Wilke, C. R. 1950 A viscosity equation for gas mixtures. J. Chem. Phys. 18, 517–519.Google Scholar
Winant, C. D. & Browand, F. K. 1974 Vortex pairing – the mechanism of turbulent mixing-layer growth at moderate Reynolds number. J. Fluid Mech. 63, 237–255.Google Scholar
Wygnanski, I. & Fiedler, H. E. 1970 The two-dimensional mixing region. J. Fluid Mech. 41, 327–361.Google Scholar
Youngs, D. L. 1984 Numerical simulation of turbulent mixing by Rayleigh–Taylor instability. Physica D 12, 32–44.Google Scholar
Zhou, Y. 2001 A scaling analysis of turbulent flows driven by Rayleigh–Taylor and Richtmyer–Meshkov instabilities. Phys. Fluids 13 (2), 538–543.Google Scholar
Zhou, Q. 2013 Temporal evolution and scaling of mixing in two-dimensional Rayleigh–Taylor turbulence. Phys. Fluids 25, 085107.Google Scholar
Zhou, Q., Huang, Y. X., Lu, Z. M., Liu, Y. L. & Ni, R. 2016 Scale-to-scale energy and enstrophy transport in two-dimensional Rayleigh–Taylor turbulence. J. Fluid Mech. 786, 294–308.Google Scholar